4.2. Метод Эйлера усовершенствованный.
Определим
в произвольной точке t
функции x(t)
производную. Сделаем шаг методом Эйлера,
определив x(t+Δt)=x(t)+
.
Вновь определим производную
в полученной точке
(t+Δt).
Рассчитав полусумму производных 0,5(
+
(t+Δt)),
сделаем полный шаг из точки t.
Проделанные операции показаны на рис
4.5. L1 –
производная в точке t,
L2 - производная в точке t+Δ t . Штрихпунктирная линия – полусумма производных.
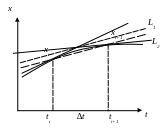
Рис.4.5
4.3. Метод Эйлера модифицированный
Определим
в произвольной точке t
функции x(t)
производную. Сделаем полшага методом
Эйлера, определив x(t+Δt/2)=x(t)+
.
Вновь определим производную
в полученной точке
(t+Δt/2).
И делаем полный шаг из точки t
вдоль этой производной
(t+Δt/2).
Проделанные операции показаны на
рис 4.6. L1
– производная в точке t,
L2 - производная в точке t+Δt/2 . Штрихпунктирная линия параллельна производной в точке t+Δt/2.
А
лгоритм
расчета по методу ЭМ запишется так:
-
производная в исходной точке.
-
производная в середине участка.
Результирующий шаг на рассматриваемом
участке:
.
Начальные условия заданы. Счет по методам ЭУ и ЭМ для звена первого порядка дает одинаковые результаты.
Рис. 4.6
4.4. Оценки порядка точности методов Эйлера (э), Эйлера модифицированного (эм) и Эйлера усовершенствованного (эу).
Наиболее удобным и почти универсальным методом оценки точности методов Рунге-Кутта является сравнение используемых алгоритмов с рядом Тейлора. Поскольку известно, что ошибка вычисления функции по ряду Тейлора не превосходит первого отброшенного слагаемого ряда.
Решаем
уравнение
методом Эйлера
.
Индексы i и i+1
означают, соответственно. моменты
времени t и t+Δt.
Разложим x(t+Δt)
в ряд Тейлора в точке t
:
(4.6)
Сравнивая
алгоритм Эйлера и алгоритм ряда Тейлора,
видим совпадение 2х слагаемых,
следовательно, порядок точности метода
Эйлера 0(Δt).В
данном случае первое отброшенное
слагаемое равно
.
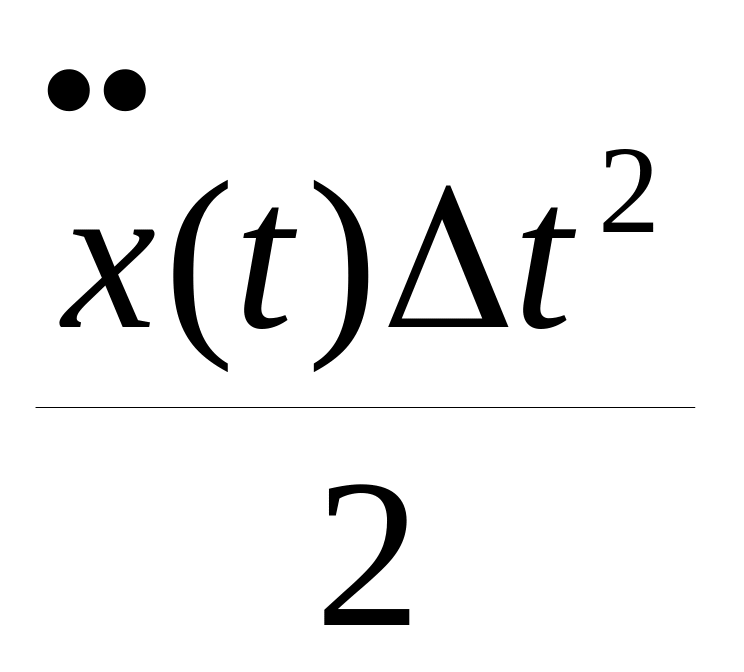Запишем
обобщенную формулу алгоритмов метода
Рунге-Кутта в виде
,
где
(4.7)
записана как полусумма производных в точках t и t+Δt , т.е. в соответствии с методом ЭМ. При этом значение x(t+Δt ) получено методом Эйлера:
.
Шаг сетки по времени равномерный:
.
Используя
обобщенный алгоритм
запишем функцию
в соответствии с методом ЭУ:
.
(4.8)
Производная взята в средней точке интервала t+Δt, а значение x в этой точке получено методом Эйлера:
.
Представим слагаемые ряда (4.6) в следующем виде:
, (4.9)
где введены
следующие обозначения:
(xi,ti)=f,
.
Чтобы оценить значения для методов ЭМ и ЭУ разложим f(x,t) в ряд Тейлора:
.
(4.10)
Используя
вместо x и t
значения xi+1
и ti+1
= ti+Δt
, определим значение
.
И, подставив ее в (4.7), получим функцию
для
метода ЭУ:
.
Подставим
ее в (4. ) и получим
. Сравним
полученное выражение с разложением в
ряд Тейлора (4.9). Совпадают три слагаемых
ряда Тейлора.
Аналогичным
образом получим функцию
для
метода ЭМ.
,
Подставив ее в обобщенный алгоритм,
увидим, что имеется совпадение с тремя
слагаемыми ряда Тейлора, поэтому точность
методов ЭМ и ЭУ имеет порядок 0(Δt2).
Приведем программы методов ЭМ и ЭУ на MATLAB:
function EylerY
x=0; t=0;
display(x)
display(t)
dt=1;
for m=1:6
dx=FunkEMY(x);
x1=x+dx*dt;
dx1=FunkEMY(x1);
x=x+0.5*(dx+dx1)*dt
t=t+dt
end
function dx=FunkEMY(x)
k=1; u=1; Tau=1;
dx=0;
dx=(k*u-x)/Tau;
function EylerM
x=0; t=0;
display(x)
display(t)
dt=1;
for m=1:6
dx=FunkEMY(x);
x1=x+0.5*dx*dt;
dx1=FunkEMY(x1);
x=x+dx1*dt
t=t+dt
end