Тема № 5 Игровые модели

I. Платежная матрица. Нижняя и верхняя цена игры.

При решении экономических задач часто приходится анализировать ситуации, в которых сталкиваются интересы двух или более конкурирующих сторон, преследующих различные цели; это особенно характерно в условиях рыночной экономики. Такого рода ситуации называются конфликтными. Математической теорией конфликтных ситуаций является теория игр. В игре могут сталкиваться интересы двух (парная игра) или нескольких (множественная игра) противников.

Стратегия – это совокупность правил, которые в зависимости от ситуации в игре определяют однозначный выбор действий данного игрока. Если в процессе игры игрок применяет попеременно несколько стратегий, то такая стратегия называется смешанной, а ее элементы – чистыми стратегиями.

Оптимальная стратегия – это такая стратегия, при использовании которой игроку обеспечивается получение максимально возможного выигрыша или минимально возможного проигрыша.

Рассмотрим конечную парную игру. 1^ый игрок имеет m стратегий: ., а 2^ой игрок – n стратегий: . Такая игра называется игрой m´n. Пусть - выигрыш игрока в ситуации, когда он выбрал стратегию , а игрок выбрал стратегию .

_{Предположим, что значения} известны для каждой пары стратегий . Составим прямоугольную таблицу, строки которой соответствуют стратегиям 1^го игрока, а столбцы – стратегиям 2^го. Если такая таблица составлена, то игра приведена к матричной форме и называется матричной игрой. Эта таблица называется платежной матрицей. Каждый элемент матрицы определяет величину выигрыша игрока и проигрыш игрока при применении соответствующих стратегий . Цель 1^го игрока – максимизировать свой выигрыш, а 2^го игрока – минимизировать свой проигрыш.

Таким образом, платежная матрица имеет вид:

Задача состоит в определении:

1. наилучшей (оптимальной) стратегии 1^го игрока из стратегий ;

2. наилучшей (оптимальной) стратегии 2^го игрока из стратегий.

Для решения задачи применяется принцип, согласно которому участники игры одинаково разумны и каждый из них делает все для того, чтобы добиться своей цели.

Нижняя цена игры (максимин) – это гарантированный выигрыш игрока при любой стратегии игрока :

,

где ;

Верхняя цена игры (минимакс) – это гарантированный проигрыш игрока при любой стратегии игрока :

,

где .

_{Справедливо неравенство .}

_{Таким образом, придерживаясь максиминной стратегии , игрок получит выигрыш не менее не зависимо от действий игрока , а 2}^ой _{игрок, придерживаясь минимаксной стратегии , гарантирует себе проигрыш не больше .}

_{Принцип, диктующий игрокам выбор соответствующих стратегий (максиминной или минимаксной), в теории игр называется принципом минимакса.}

_{Существуют матричные игры, для которых нижняя цена игры равна верхней, т. е. .}

_{Такие игры называются играми с седловой точкой, в этом случае называется чистой ценой игры.}

_{Пример 5.1. Пусть дана платежная матрица. Найти решение игры, т. е. определить нижнюю и верхнюю цены игры и минимаксные стратегии.}

_{Решение.}

.

Таким образом, нижней цене игры соответствует стратегия 1^го игрока. Выбирая эту стратегию, он достигнет выигрыша не менее 4 при любом поведении 2^го игрока. Верхней цене игры соответствует стратегия 2^го игрока - . Эти стратегии являются минимаксными. Если обе стороны будут придерживаться этих стратегий, то выигрыш будет равен 4, что соответствует элементу платежной матрицы .

Задание. Определить нижнюю и верхнюю цены игры, минимаксные стратегии и оптимальные решения игры, если существует седловая точка.

5.1. 5.2.

3. 5.4.

5.5. 5.6.

II. Доминирование стратегий.

Стратегия будет доминирующей для 1^го игрока, а стратегия доминируемой, если выполнено равенство для всех индексов .

Стратегия для 2^го игрока является доминирующей, а стратегия доминируемой, если выполнено неравенство для всех индексов .

Доминируемые стратегии можно исключать из платежной матрицы, так как они заведомо не выгодны для игрока.

Пример 5.2. Исключить доминируемые стратегии игроков.

.

Решение. Замечаем, что все элементы третьего столбца больше элементов второго столбца матрицы, а также элементы четвертого столбца больше элементов второго столбца, то есть стратегии и являются доминируемыми стратегиями, а значит, их можно исключить. Получаем матрицу

.

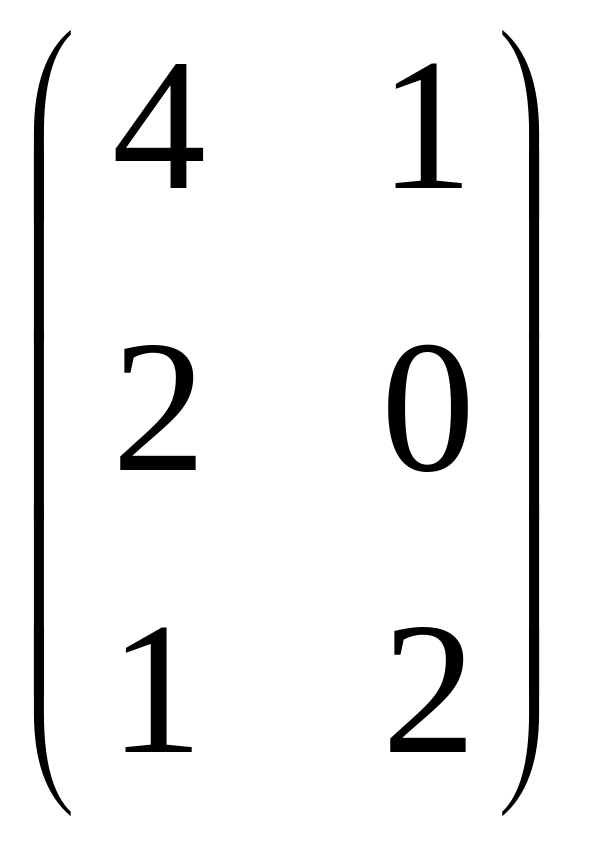Далее очевидно, что элементы второй строки полученной матрицы меньше элементов первой строки, поэтому стратегия является доминируемой. Окончательно получаем

.

Задание. Упростить платежную матрицу,:

5.6. 5.7.

5.8. 5.9

5.10.

III. Решение игр в смешанных стратегиях аналитическим и геометрическим способом.

Если игра не имеет седловой точки, то применение чистых стратегий не дает оптимального решения игры. В таком случае можно получить оптимальное решение, случайным образом, чередуя чистые стратеги.

Смешанной стратегией игрока называется применение чистых стратегий с вероятностями , причем сумма вероятностей равна 1: . Смешанные стратегии игрока записываются в виде строки . Аналогично смешанные стратегии игрока обозначаются , где сумма вероятностей появления стратегий равна 1: .

Рассмотрим игру размера 2x2, которая является простейшим случаем конечной игры. Если такая игра имеет седловую точку, то оптимальное решение — это пара чистых стратегий, соответствующих этой точке.

В игре, в которой отсутствует седловая точка, в соответствии с основной теоремой теории игр оптимальное решение существует и определяется парой смешанных стратегий и .

Пусть игра задана платежной матрицей

.

Средний выигрыш игрока , если он использует оптимальную смешанную стратегию , а игрок - чистую стратегию (это соответствует 1^му столбцу платежной матрицы ), равен цене игры :

.

Тот же выигрыш получает игрок , если 2^ой игрок применяет стратегию , т. е. . Учитывая, что , получаем систему уравнений для определения оптимальной стратегии и цены игры :

(5.1)

Решая эту систему, получим оптимальную стратегию

,

и цену игры

.

При отыскании - оптимальной стратегии игрока , получаем, что при любой чистой стратегии игрока ( или ) средний проигрыш игрока равен цене игры , т. е.

(5.2)

Тогда оптимальная стратегия определяется формулами:

,

.

Пример 5.3. Игра задана платежной матрицей: . Найти решение игры в смешанных стратегиях аналитическим способом.

Решение. Так как седловая точка отсутствует ( , ), поэтому ищем решение в смешанных стратегиях. Для игрока средний выигрыш равен цене игры (при и ); для игрока средний выигрыш равен цене игры ( и ). Системы уравнений (5.1) и (5.2) в данном случае имеют вид:

Решая эти системы, получаем .

Это означает, что оптимальная стратегия каждого игрока состоит в том, чтобы чередовать свои чистые стратегии случайным образом, выбирая каждую из них с вероятностью , при этом средний выигрыш равен 0.

Решение игры 22 допускает наглядную геометрическую интерпретацию.

Пусть игра задана платежной матрицей

.

По оси абсцисс отложим единичный отрезок (рис. 5.1.); точка изображает стратегию , а все промежуточные точки этого отрезка – смешанные стратегии 1^го игрока. На вертикальной оси ординат откладываются выигрыши при стратегии (то есть числа ), на вертикальной оси II-II (рис 5.1.) выигрыши при стратегии (числа ). Точки на вертикальной оси, соответствующие проигрышу 2^го игрока при применении им первой стратегии обозначим и соединим прямой. Аналогично для второй стратегии 2^го игрока.

В соответствии с принципом минимакса оптимальная стратегия такова, что минимальный выигрыш игрока (при наихудшем поведении игрока ) обращается в максимум. Ординаты точек, лежащих на ломаной (рис. 5.1.), показывают минимальный выигрыш игрока при использовании им любой смешанной стратегии. Оптимальную стратегию определяет точка , в которой минимальный выигрыш достигает максимума; её ордината равна цене игры .

Пример 5.4. Решить игру, заданную платежной матрицей

Решение. Откладываем на оси абсцисс единичный отрезок . На вертикальной оси ординат откладываем отрезки , соответствующий стратегии , и , соответствующий стратегии . На вертикальной оси II-II отрезок соответствует стратегии , отрезок соответствует стратегии (см. рис. 5.2).

1

Рис. 5.1 Решение игры 22 графическим методом

Нижняя цена игры , верхняя цена игры . Седловая точка отсутствует. Из рис. 5.2. видно, что абсцисса точки определяет оптимальную стратегию , а ордината – цену игры . Точка является точкой пересечения прямых и .

В общем виде уравнение прямой, проходящей через две точкии с координатами и записывается следующим образом: . Тогда уравнение прямой , проходящей через точки и :

, откуда .

Уравнение прямой , проходящей через точки и :

, или .

Решая систему уравнений:

получим координаты точки : . Тогда ; ; , то есть смешанная стратегия 1^го игрока имеет вид: , а цена игры . Это означает, что тактика 1^го игрока заключается в применении первой стратегии с вероятностью 0,4, а второй с вероятностью 0,6.

у

II

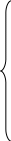
N

II

х

Рис. 5.2. Пример решения игры графическим методом

Задание. Найти решение игры аналитическим и геометрическим методами.

5.11. 5.12. 5.13.

5.14. 5.15.

IV. Сведение игры к задаче линейного программирования.

Пример 5.4. Предприятие может выпускать три вида продукции , получая при этом прибыль, зависящую от спроса, который может быть в одном из четырех состояний . Дана матрица, элемент которой характеризует прибыль, которую получит предприятие при выпуске -ой продукции с -ым состоянием спроса: .

Определить оптимальные пропорции, гарантирующие среднюю величину прибыли при любом состоянии спроса.

Решение. Замечаем, что 2^ая стратегия 2^го игрока является дублируемой 1^ой стратегией, значит, ее можно исключить. Тогда преобразованная матрица примет вид: . Так как нижняя цена игры не равна верхней цене игры , то решение игры ищем в смешанных стратегиях: , .

Обозначим , где - цена игры. Составим две взаимно-двойственные задачи линейного программирования. Для оптимальной стратегии 1^го игрока все средние выигрыши (то есть элементы -го столбца платежной матрицы почленно умножаются на соответствующие вероятности выбора стратегий 1^го игрока и результаты складываются) не меньше цены игры. В силу введенных обозначений, получаем:

Цель игрока - максимизировать свой гарантированный проигрыш, то есть цену игры. Максимизация цены игры эквивалентна минимизации величины . Поэтому целевая функция запишется следующим образом:

.

Для оптимальной стратегии 2^го игрока все средние проигрыши не больше цены игры, а цель игрока - минимизировать свой проигрыш (т.е. максимизировать величину ). Тогда задача линейного программирования запишется следующим образом:

Решив одну из двух задач симплекс-методом, другую можно решить, применив свойства двойственных оценок. Получим , . Это означает, что оптимальные пропорции выпуска продукции, гарантирующие среднюю величину прибыли – это 40% продукции 1^го вида и 60% 3^го. Оптимальный спрос находится в 20% в состоянии и в 80% в состоянии .

Задание. Найти решение игры путем сведения ее к задаче линейного программирования.

5.16. 5.17. 5.18.

5.19. 5.20.

V. Применение различных критериев при решении игр с природой.

Под природой понимается вся совокупность внешних обстоятельств, в которых принимается решение первым игроком.

Пусть - возможные чистые стратегии 1^го игрока; - возможные состояния природы (среды). И пусть - выигрыш (последствие) 1^го игрока при применении им своей -ой чистой стратегии и при -ом состоянии среды. Тогда такая игра записывается в виде платежной матрицы:

Для нахождения оптимального решения игры с природой используется ряд критериев.

1. Критерий Вальда основывается на принципе пессимизма:

При выборе решения надо рассчитывать на самый худший вариант. Оптимальной в этом случае будет стратегия , если для некоторого элемента выполнено равенство:

,

то есть элемент является нижней ценой игры.

2. Критерий Гурвица заключается в следующем:

При любом выборе стратегии наихудший для принимающего решения вариант реализуется с вероятностью , а наилучший с вероятностью , где - показатель пессимизма . Оптимальной в этом случае будет стратегия , если для некоторого элемента выполнено равенство:

(5.3)

3. Критерий Сэвиджа также является критерием крайнего пессимизма.

Для использования этого критерия вводится матрица рисков , ( ) элементы которой определяются по формуле:

,

(5.4)

где - максимальный элемент в столбце.

Оптимальной считается та стратегия , которая минимизирует максимальный риск, то есть для элемента матрицы выполнено равенство:

.

4. Критерий максимизации среднеожидаемого выигрыша используется, в случае, когда заданы вероятности наступлений состояний среды: . Тогда оптимальной будет стратегия , если для некоторого элемента выполнено условие:

,

где .

5. Критерий минимизации среднеожидаемого риска также используется, если известны вероятности наступлений состояний среды. В этом случае стратегия будет оптимальной, если для элемента матрицы риска выполнено условие:

где .

Замечание. Оптимальные стратегии по критерию максимизации среднеожидаемого выигрыша и минимизации среднеожидаемого риска совпадают.

Пример 5.5. Энергетическая компания должна выбрать проект электростанции. Всего имеется четыре типа электростанций: - тепловые, - приплотинные, - безшлюзовые, - шлюзовые. Последствия, связанные со строительством и дальнейшей эксплуатацией электростанции каждого из этих типов, зависят от ряда неопределенных факторов (состояния погоды, возможности наводнения, цены топлива и др.). Предположим, что можно выделить четыре варианта сочетаний данных факторов – они выступают в качестве состояний среды и обозначены через и . Вероятности наступления этих состояний равны соответственно 0,32; 0,12; 0,27 и 0,29. Экономическая эффективность электростанции определяется в данном случае как процент прироста дохода в течение одного года эксплуатации электростанции в сопоставлении с капитальными затратами. Она зависит как от типа электростанции, так и от состояния среды и определяется матрицей:

Определить какой проект электростанции является оптимальным, если коэффициент пессимизма ?

Решение.

1. В соответствии с критерием Вальда найдем минимальное число в каждой строчке матрицы, то есть выберем для каждого проекта электростанции наихудшее состояние среды:

,

,

,

.

Далее в соответствии с принципом минимакса среди этих чисел выбираем максимальное:

,

то есть оптимальной стратегией по критерию Вальда является выбор 2^го проекта электростанции (так как ).

2. Оптимальную по критерию Гурвица стратегию находим, используя формулу (5.3):

, , , .

Выбираем максимальное среди этих чисел:

,

то есть . Значит по критерию Гурвица с коэффициентом пессимизма оптимальным является третий проект электростанции.

3. Для применения критерия Сэвиджа построим матрицу рисков по формуле (5.4). Найдем сначала числа :

,

,

,

.

Тогда

Далее ищем в каждой строчке матрицы рисков максимальное число:

,

,

,

.

Минимум достигается для стратегий и .

4. Определим оптимальную стратегию по критерию максимизации среднеожидаемого выигрыша, используя заданные вероятности наступления состояний природы. Найдем среднеожидаемый выигрыш для каждой стратегии:

,

,

,

.

Максимальный среднеожидаемый выигрыш достигается для четвертой стратегии.

5. Для определения оптимальной стратегии по критерию минимизации среднеожидаемого риска используются вероятности наступлений состояний среды и элементы матрицы риска. Находим для каждой стратегии среднеожидаемый риск:

,

,

,

.

Минимальный среднеожидаемый риск достигается также для четвертой стратегии.

Задание. В игре с природой с платежной матрицей вероятности наступления состояний природы равны соответственно . Найти оптимальную стратегию 1^го игрока, используя критерии оптимальности Вальда, Гурвица, Сэвиджа, максимизации среднеожидаемого выигрыша и минимизации среднеожидаемого риска.

5.21. 5.22.

5.23. 5.24.

5.25. 5.26.