
Лекция № 7
1.8. Алгоритм симплекс-метода поиска оптимального решения злп
Алгоритм начинает работать с некоторого начального допустимого базиса В1 (x(В1)≥0) и соответствующего базисного множества N(В1). Пусть k – номер итерации алгоритма.
Шаг
1.
![]()
Шаг 2. Для базиса Вk формируются B, с(Bk) и осуществляется расчет B-1, A(Bk) (1.39), b(Bk) (1.47) и Dс (1.75) .
Шаг 3.Проверка условия оптимальности базисного решения (1.78).
Если условие оптимальности выполняется, то определяется оптимальное решение:
![]() (1.84)
(1.84)
и завершается работа алгоритма.
Шаг 4. Выбор номера столбца l, вводимого в базис (1.82).
Шаг
5. Проверка условия
![]() (1.83):
(1.83):
Если условия неограниченности выполняются, то работа алгоритма завершается.
Шаг 6. Определение номера столбца r, выводимого из базиса (1.62) ÷ (1.64).
Шаг 7. Корректировка базиса (1.67):
![]() . (1.85)
. (1.85)
Шаг 8. k:=k+1, переход на шаг 2.
Представленный алгоритм не является эффективным в вычислительном отношении.
Основной объем вычислений связан с выполнением второго пункта алгоритма. При большой размерности ЗЛП по числу ограничений основная вычислительная проблема состоит в расчете В-1. Можно показать, что основные компоненты структуры данных ЗЛП (B-1, A(Bk), b(Bk) и др.) при переходе от одной итерации алгоритма к другой можно не рассчитывать каждый раз заново, а пересчитывать итерационно на основе рекуррентных соотношений Гаусса-Жордана.
1.9. Преобразования Гаусса-Жордана
Рассмотрим два соседних допустимых базиса Bk и Bk+1, полученных на соседних итерациях алгоритма симплекс-метода (связь между ними определяется соотношением
![]() . (1.85)
. (1.85)
Этим базисам соответствуют две обратные базисные матрицы B-1k и B-1k+1. Если умножить слева систему основных ограничений ЗЛП
![]() на каждую из этих
матриц, то с учетом (1.39) и (1.47) получим
следующие соотношения:
на каждую из этих
матриц, то с учетом (1.39) и (1.47) получим
следующие соотношения:
![]() , (1.86)
, (1.86)
![]() , (1.87)
, (1.87)
которые можно рассматривать как эквивалентные системы линейных уравнений, полученные с помощью линейных преобразований исходных ограничений. Следовательно, существуют эквивалентные линейные преобразования системы уравнений (1.86) в (1.87).
Для того, чтобы определить правила этих преобразований, рассмотрим структуру матриц A(Bk) и A(Bk+1), выделим в них и сравним между собой базисные столбцы (рис.1.16).

Рис. 1.16
Отличия
наблюдаются лишь в столбцах al(B)
и
![]() :
в матрице A(Bk)
столбец
al(Bk),
не входящий в базис Bk,
имеет произвольную структуру, а в матрице
A(Bk+1)
такую
произвольную структуру имеет столбец
:
в матрице A(Bk)
столбец
al(Bk),
не входящий в базис Bk,
имеет произвольную структуру, а в матрице
A(Bk+1)
такую
произвольную структуру имеет столбец
![]() ,
выведенный из базиса. С другой стороны,
,
выведенный из базиса. С другой стороны,
![]() и таким же должен стать столбец
и таким же должен стать столбец
![]() ,
так как он занимает r-ое
место во вновь образованном базисе.
,
так как он занимает r-ое
место во вновь образованном базисе.
Отличия столбцов
al(Bk)
и al(Bk+1)
однозначно
определяют следующий алгоритм линейных
преобразований системы уравнений (1.86)
в систему (1.87). В этих преобразованиях
r-ая
строка носит называние «разрешающая
строка», l-ый
столбец – «разрешающий столбец», а
![]() - «разрешающий элемент»:
- «разрешающий элемент»:
В системе уравнений (1.86) r-ое уравнение необходимо разделить на коэффициент
 (обеспечивается равенство
(обеспечивается равенство
 ).
).Все остальные i-ые уравнения системы (1.87) получаются в результате следующих преобразований:
Преобразованное в п.1. r-ое уравнение умножается на коэффициент
 .
.Полученное в п.2.1 r-ое уравнение вычитается из преобразуемого в составе (1.86) i-ого уравнения (обеспечивается выполнение равенства
 для всех
для всех
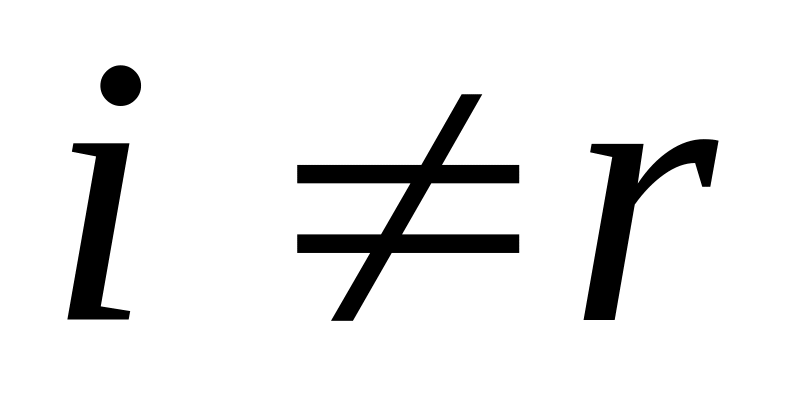 ).
).
Правила этого алгоритма и составляют суть преобразований Гаусса-Жордана. Можно сформулировать достаточно простые, показанные на рис.1.17 мнемонические правила, соответствующие этим преобразованиям.

Рис. 1.17
Формальные соотношения преобразований Гаусса-Жордана могут быть записаны следующим образом:
 ,
,
![]()
для
![]()
![]() (
(![]()
![]() ); (1.88)
); (1.88)
 для
всех
для
всех

![]() ;
;
для всех
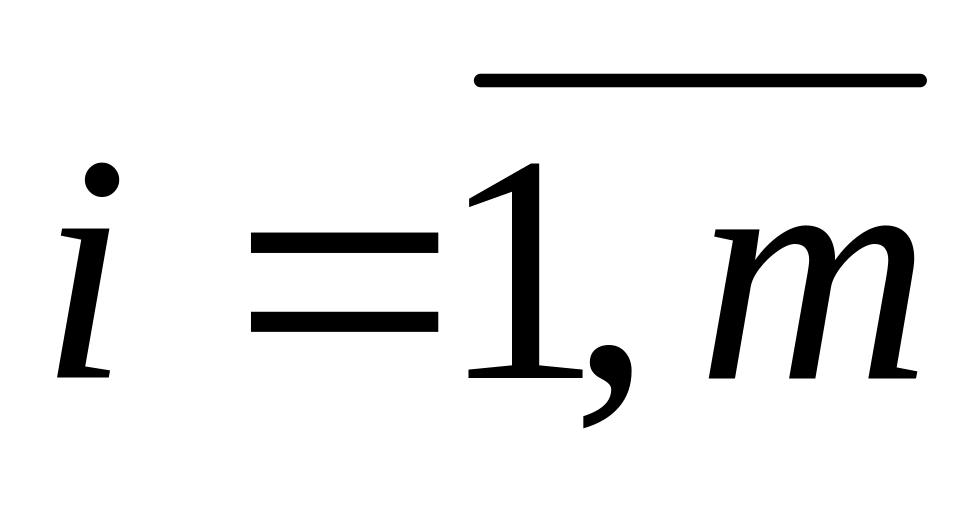 (
( ).
).
Необходимо отметить, что при машинной реализации этих преобразований порядок пересчета вначале общих элементов, а затем элементов разрешающей строки и разрешающего столбца является принципиально важным, так как новые значения коэффициентов в соответствующих структурах данных заменяют старые. Пересчитав же сначала элементы разрешающего столбца и (или) разрешающей строки и, следовательно, потеряв их старые значения, невозможно пересчитать общие элементы.
Не трудно заметить,
что с помощью преобразований Гаусса-Жордана
можно пересчитывать и расширенные
структуры данных
![]() ,
,
![]() ,
рассматривая последнюю строку уравнений
,
рассматривая последнюю строку уравнений
![]() ,
как эквивалентно преобразованное
уравнение гиперплоскости, формируемое
из целевой функции ЗЛП.
,
как эквивалентно преобразованное
уравнение гиперплоскости, формируемое
из целевой функции ЗЛП.
Можно также
показать, что по тем же самым
правилам преобразуется и матрица
![]() относительно присоединенного разрешающего
столбца
относительно присоединенного разрешающего
столбца
![]() (рис.1.18).
(рис.1.18).

Рис.1.18
Формальные соотношения для этого случая предлагается написать самостоятельно.
На использовании преобразований Гаусса-Жордана основаны обсуждаемые ниже алгоритмы симплекс-таблиц поиска оптимального решения ЗЛП.
