Тема 5.2. Методы оценки системы одновременных уравнений.

Решение типовых задач

Задача 1. Имеется следующая структурная точно идентифицируемая модель:

Исходя из приведенной формы модели уравнений

определите структурные коэффициенты модели.

Решение:

Первое уравнение: из третьего уравнения приведенной формы выразим x₂ (так как его нет в первом уравнении структурной формы):

Данное выражение содержит переменные y₃,x₁,x₃, которые нужны для первого уравнения структурной формы модели (СФМ). Подставим полученное выражение x₂ в первое уравнение приведенной формы модели (ПФМ):

- первое уравнение СФМ.

Второе уравнение: в нем нет переменных x₁ и x₃. Структурные параметры второго уравнения СФМ можно будет определить в два этапа:

Первый этап: выразим x₁ в данном случае из первого или третьего уравнения ПФМ. Например, из первого уравнения:

Подстановка данного выражения во второе уравнение ПФМ не решила бы задачу до конца, так как в выражении присутствует x₃, которого нет в СФМ.

Выразим x3 из третьего уравнения ПФМ:

Подставим его в выражение x₁:

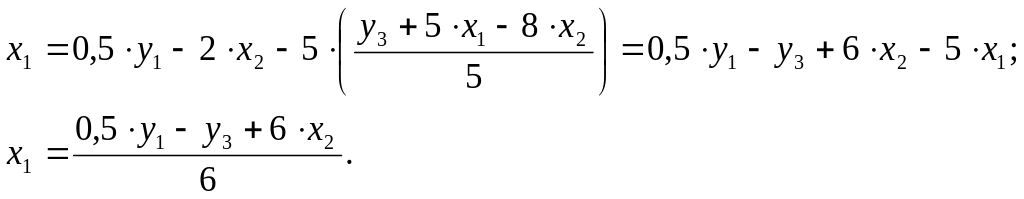
Второй этап: аналогично, чтобы выразить x₃ через искомые y₁, y₃ и x₂, заменим в выражении x₃ значение x₁ на полученное из первого уравнения ПФМ:

Следовательно,

Подставим полученные x₁ и x₃ во второе уравнение ПФМ:

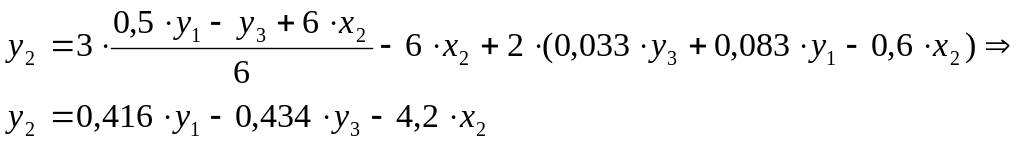
• второе уравнение СФМ.

Третье уравнение: из второго уравнения ПФМ выразим x2, так как его нет в третьем уравнении СФМ:

Подставим полученное выражение в третье уравнение ПФМ:

- третье уравнение СФМ.

Таким образом, СФМ примет вид:

Задача 2. Имеется следующая точно идентифицируемая структурная модель:

Соответствующая ей приведенная форма модели имеет вид:

Задание: Определить неизвестные параметры структурной модели.

Решение: Для идентифицируемых систем методом оценки структурных параметров является косвенный МНК. Он заключается в том, что уравнения приведенной формы модели (ПФМ), полученные обычным МНК как уравнения множественной регрессии, с помощью алгебраических преобразований превращаются в уравнения структурной формы модели (СФМ). Здесь, как видим, МНК применяется только один раз – для оценки коэффициентов приведенной формы.

Начнем с построения первого уравнения СФМ. Из всех уравнений ПФМ к нему ближе всех по структуре первое уравнение: в обоих уравнениях слева стоит y₁, а справа стоят х₁ и х₂. Однако они отличаются тем, что в первом уравнении ПФМ стоит х₃, а в первом уравнении СФМ стоит y₂. Поэтому, чтобы получить первое уравнение СФМ из первого уравнения ПФМ, надо в последнем заменить х₃ на выражение, в котором появилась бы y₂. Эту замену делаем с помощью второго уравнения ПФМ:

Подставим в первое уравнение ПФМ, получаем после элементарных преобразований:

,

или

.

Это и есть первое уравнение СФМ.

Для получения третьего уравнения СФМ действуем аналогично: в третьем уравнении ПФМ заменяем х₂ так, чтобы в результате замены появилась y₂. такую замены также делаем через второе уравнение ПФМ:

.

Подставим в третье уравнение ПФМ, получаем:

,

или

.

Это и есть третье уравнение СФМ.

Для получения второго уравнения СФМ требуются более сложные преобразования. Это связано с тем, что из второго уравнения ПФМ, как наиболее похожего на второе уравнение СФМ, надо исключить сразу две переменные – х₁ и х₃, чтобы при этом появились y₁ и y₃.. Последовательное исключение здесь не годится, их надо исключать одновременно. Для этого запишем первое и третье уравнения ПФМ как систему относительно исключаемых переменных:

Решаем эту систему любым способом, например, например, методом определителей:

Подставим полученные решения во второе уравнение ПФМ, получаем второе уравнение СФМ:

или

.

Теперь можем полностью записать структурную модель:

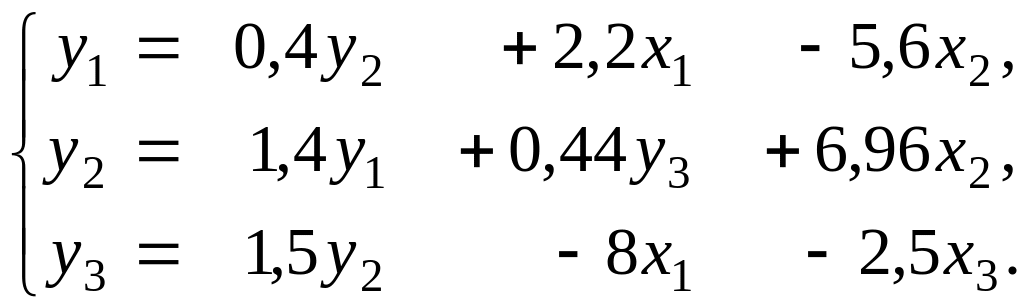
Задача 3. Имеется структурная модель:

Для нее записана приведенная форма модели:

Задание: оценить структурные коэффициенты модели.

Решение: На основе второго уравнения приведенной формы модели можно найти теоретические значения для эндогенной переменной , т.е. . Подставим в это уравнение значения и в форме отклонений от средних значений, запишем в виде таблицы:

- 1,4	-0,4	0,103	-1,297	- 2	2,594	1,682
- 0,4	-2,4	0,042	-0,358	- 1	0,358	0,128
0,6	-1,4	- 0,035	0,565	0	0	0,319
- 0,4	1,6	0,02	-0,38	1	- 0,38	0,144
1,6	2,6	- 0,13	1,47	2	2,94	2,161
0	0	0	0	0	5,512	4,434

После того, как найдены оценки заменим в уравнении фактические значения их оценками найдем значения новой переменной Применим МНК к уравнению:

.

Получим:

В целом рассматриваемая система будет иметь вид:

Задача 4. Система структурных уравнений имеет вид:

т.е. является сверхидентифицируемой.

В этом случае матрицы эндогенных и экзогенных переменных имеют вид:

.

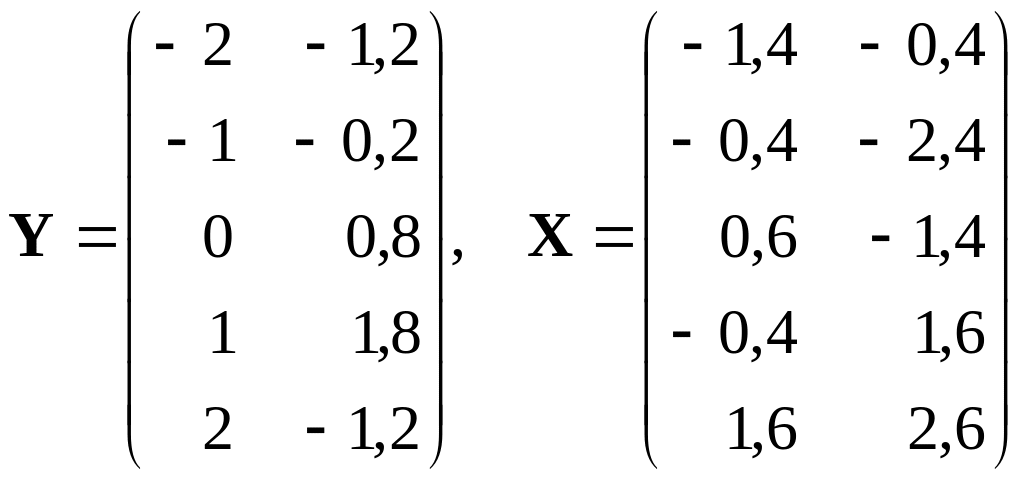Важная для расчетов матрица сумм попарных произведений факторов равна:

.

Матрицы значений переменных в правых частях уравнений следующие:

,

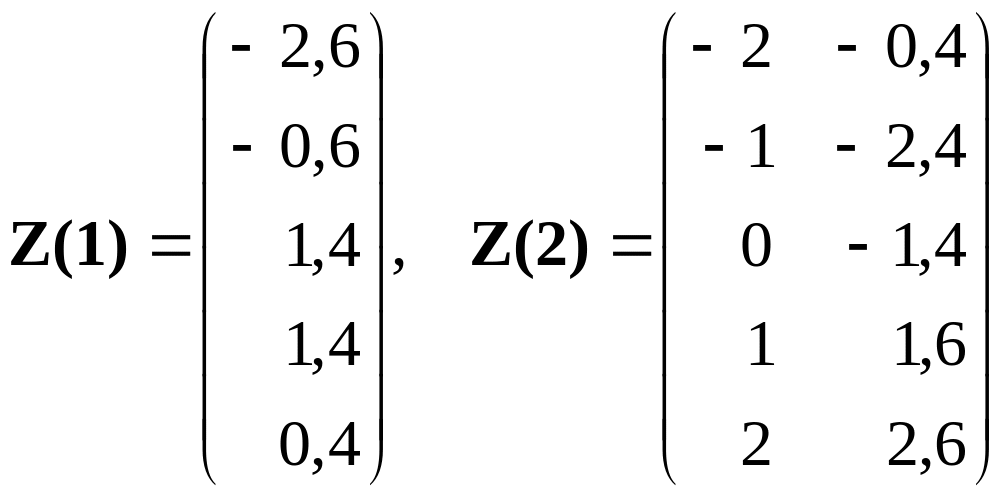причем в матрице записаны значения , а в - значения переменных y₁ и x₂, которые присутствуют в правых частях соответствующих уравнений.

Отсюда вспомогательные матрицы и равны:

; .

Соберем матрицу из этих блоков и транспонируем её:

, .

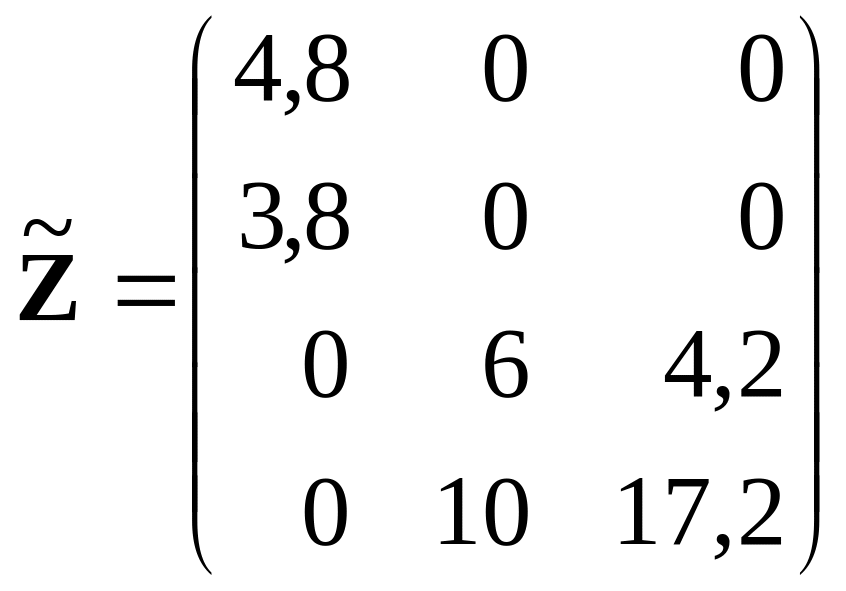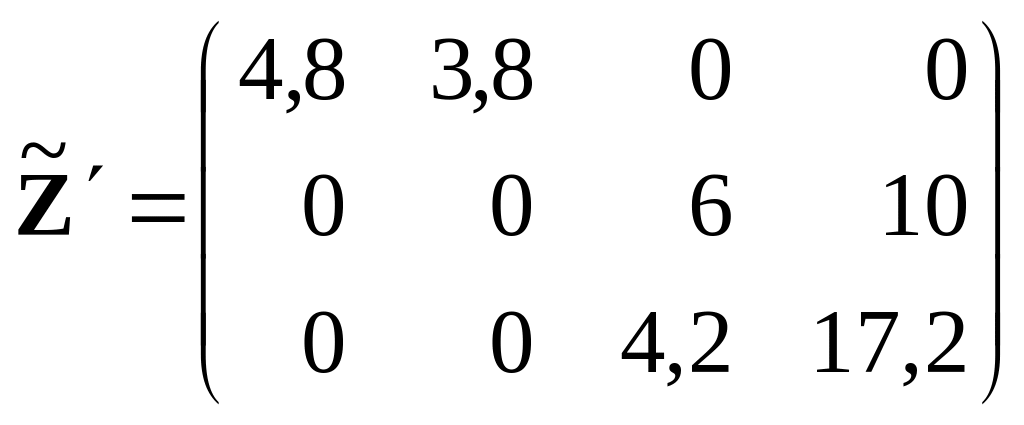Построим оценку матрицы ковариаций случайных возмущений структурной формы:

.

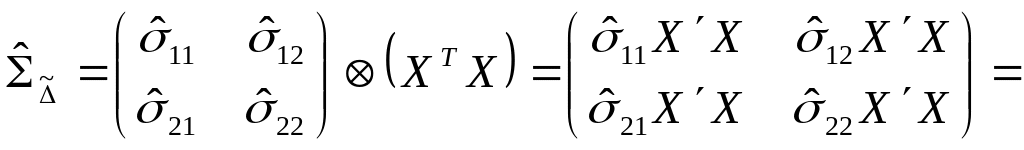
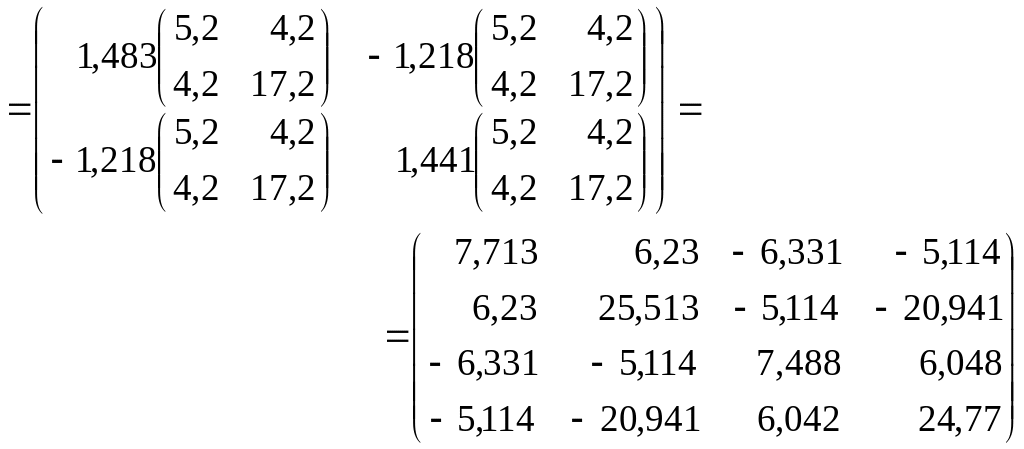В последнем выражении значок  обозначает операцию тензорного произведения двух матриц, в результате которой получается матрица, состоящая из блоков, которые состоят из произведений элементов первой матрицы на всю вторую матрицу.

Находим обратную к ней:

.

Необходимая для расчетов матрица собирается из следующих блоков:

;

.

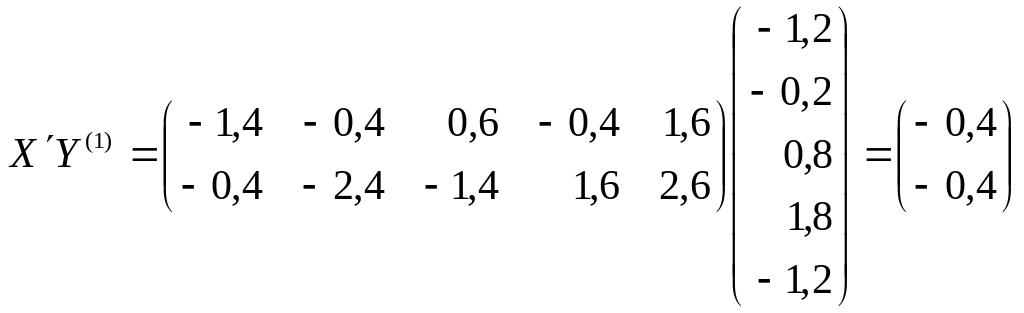Отсюда

.

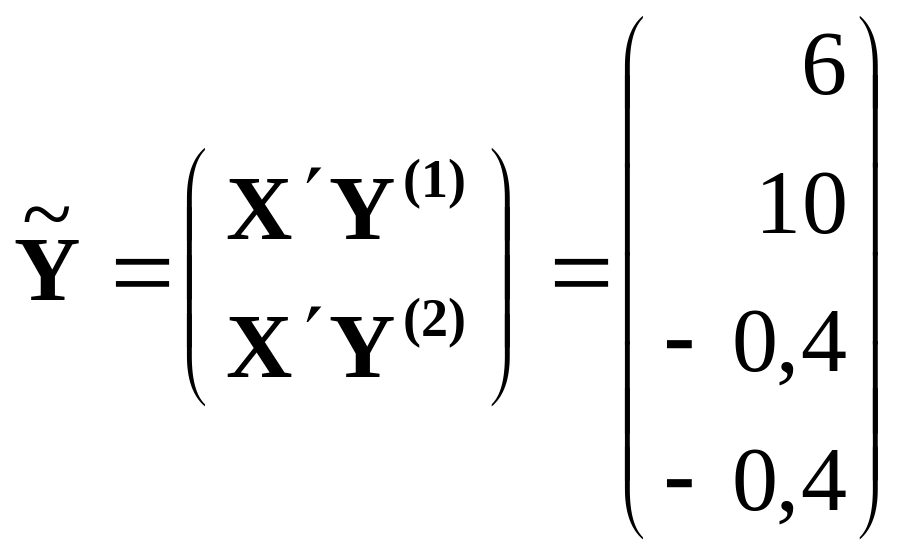Структурные параметры уравнений записываются так:

.

Отсюда

= =

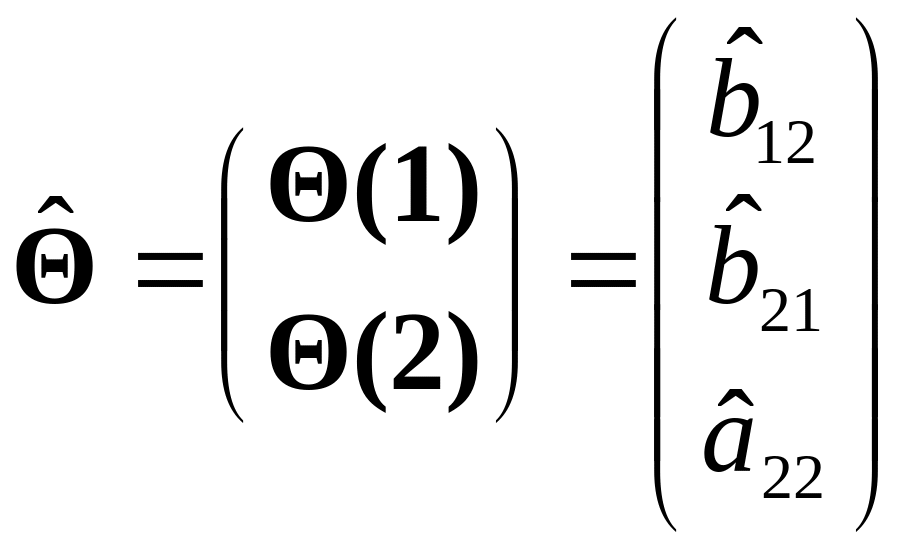Тогда систему уравнений с оцененными параметрами запишем так: