
![]() .
.
Решение. Корень
![]() многочлена
многочлена
![]() имеет кратность, равную
имеет кратность, равную
![]() ,
тогда и только тогда, когда в разложении
многочлена
по степеням
,
тогда и только тогда, когда в разложении
многочлена
по степеням
![]() коэффициенты
коэффициенты
![]() ,
а
,
а
![]() .
.
Значит, чтобы решить поставленную задачу, надо построить схему Горнера для разложения многочлена по степеням и посмотреть сколько нулей подряд в разложении. Это количество нулей и будет кратность корня .
5. Неприводимые многочлены над полем
Многочлен
натуральной степени
![]() называется приводимым над полем
называется приводимым над полем
![]() ,
если над этим полем существуют два
многочлена
,
если над этим полем существуют два
многочлена
![]() и
и
![]() натуральной степени такие, что
натуральной степени такие, что
![]() .
.
Многочлен натуральной степени называется неприводимым над полем , если над этим полем нельзя подобрать многочлены и натуральной степени такие, что .
Задача 19.
Является ли приводимым многочлен
![]() над
над
![]() .
.
Решение.
1
способ.
Если над
существуют многочлены
и
натуральной степени такие, что
,
то они могут быть только определенной
истинной степени:
![]() ,
,
![]() .
Но тогда
.
Но тогда
![]() ,
,
![]()
![]() .
Используем метод неопределенных
коэффициентов для нахождения
.
Используем метод неопределенных
коэффициентов для нахождения
![]() .
.
![]() ,
то есть
,
то есть
![]() ,
,
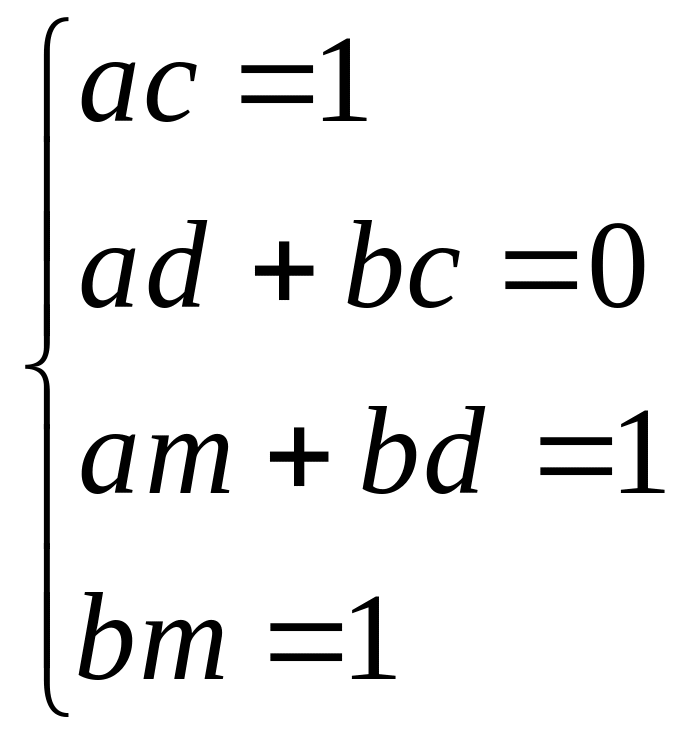 в
в ![]() .
.
Имеем:
![]() ,
то есть
,
то есть
![]() ,
,
![]() ,
то есть
,
то есть
![]() .
Всего получается 4 четверки
.
Всего получается 4 четверки
![]() для нахождения
для нахождения
![]() из системы:
из системы:
![]()
(1)
![]() ,
т. е.
,
т. е.
![]() ,
откуда
,
откуда
![]()
![]() не является решением
исходной системы.
не является решением
исходной системы.
(2)
![]() ,
т. е.
,
т. е.
![]() ,
откуда
,
откуда
![]() является решением
исходной системы, т. е.
является решением
исходной системы, т. е.
![]() ,
,
![]() и
.
и
.
Следовательно многочлен является приводимым над полем .
2 способ.
Если над
![]() многочлен приводим, то он представлен
в виде произведения линейного двучлена
и многочлена второй степени:
многочлен приводим, то он представлен
в виде произведения линейного двучлена
и многочлена второй степени:
![]() , где
, где
![]() .
.
Но означает, что
![]() является корнем многочлена
.
Значения
является корнем многочлена
.
Значения
![]() .
Проверим каждое из них:
.
Проверим каждое из них:
![]()
![]() ,
где
,
где
![]() .
Следовательно,
является приводимым над
многочленом.
.
Следовательно,
является приводимым над
многочленом.
6. Критерий Эйзенштейна
Многочлен
с рациональными коэффициентами неприводим
над полем
![]() тогда и только тогда, когда над этим
полем неприводим многочлен с целыми
коэффициентами, полученный умножением
на общее наименьшее кратное знаменателей
всех его коэффициентов.
тогда и только тогда, когда над этим
полем неприводим многочлен с целыми
коэффициентами, полученный умножением
на общее наименьшее кратное знаменателей
всех его коэффициентов.
Пусть
![]() ,
,
![]() - многочлен с целыми коэффициентами.
- многочлен с целыми коэффициентами.
Критерий
Эйзенштейна:
Если существует такое простое число
![]() ,
что старший коэффициент многочлена
,
что старший коэффициент многочлена
![]() не делится на
,
все остальные коэффициенты делятся на
,
а младший коэффициент
не делится на
,
все остальные коэффициенты делятся на
,
а младший коэффициент
![]() ,
делится на
,
не делится на
,
делится на
,
не делится на
![]() ,
то многочлен
неприводим над полем
.
,
то многочлен
неприводим над полем
.
Заметим, что эта теорема является достаточным условием неприводимости многочлена над .
Задача 20.
Проверить, является ли неприводимым
над
многочлен
![]() .
.
Решение.
Здесь подходит
число
![]() .
Действительно,
.
Действительно,
![]() не делится на 2,
не делится на 2,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() не делится на
не делится на
![]() .
Значит,
неприводим над
.
.
Значит,
неприводим над
.
Задача 21. Приводим
ли над
многочлен
![]() .
.
Решение. К
этому многочлену критерий Эйзенштейна
непосредственно применить нельзя. Но
сделаем замену
![]() ,
в результате которой получается многочлен
,
в результате которой получается многочлен
![]() ,
неприводимый в силу критерия Эйзенштейна
(
,
неприводимый в силу критерия Эйзенштейна
(![]() ).
Следовательно, и многочлен
неприводим над
.
).
Следовательно, и многочлен
неприводим над
.
7. Наибольший общий делитель двух многочленов и его свойства
![]() –
это такой многочлен
,
который делит
и
и сам делится на любой общий делитель
многочленов
и
.
Для данных многочленов
и
над полем
существует столько наибольших общих
делителей, сколько элементов в поле
минус 1.
–
это такой многочлен
,
который делит
и
и сам делится на любой общий делитель
многочленов
и
.
Для данных многочленов
и
над полем
существует столько наибольших общих
делителей, сколько элементов в поле
минус 1.
Все наибольшие
общие делители многочленов
и
различаются только скалярным множителем
![]() .
.
Среди всех общих
наибольших делителей многочленов
и
выделяют один – старший коэффициент
которого равен
![]() .
Этот многочлен называют нормированным
общим наибольшим делителем многочленов
и
.
.
Этот многочлен называют нормированным
общим наибольшим делителем многочленов
и
.
можно найти по определению.
Задача 22. Найти
для
![]() и
и
![]() над
над
![]() .
.
Решение. Многочлен
делится на все многочлены вида
![]() ,
,
![]() ,
(
,
(![]() ),
на все многочлены вида
),
на все многочлены вида
![]() ,
,
![]() ,
(
,
(![]() ),
на все многочлены вида
),
на все многочлены вида
![]() ,
,
![]() ,
(
,
(![]() ),
на все многочлены вида
),
на все многочлены вида
![]() ,
,
![]() ,
(
,
(![]() ).
Многочлен
делится на все многочлены вида
).
Многочлен
делится на все многочлены вида
![]() ,
,
![]() ,
(
,
(![]() ),
и на все многочлены вида
),
и на все многочлены вида
![]() ,
,
![]() ,
(
,
(![]() ).
Общими делителями многочленов
и
являются все многочлены вида
).
Общими делителями многочленов
и
являются все многочлены вида
![]() ,
,
![]() ,
(
)
и все многочлены вида
,
(
)
и все многочлены вида
![]() ,
,
![]() ,
(
,
(![]() ).
Среди них делятся на все общие делители
многочленов
и
только многочлены вида
).
Среди них делятся на все общие делители
многочленов
и
только многочлены вида
![]() ,
,
(
).
Значит, они и являются общими делителями
многочленов
и
.
Их бесконечно много. Среди них выделяется
нормированный
,
,
(
).
Значит, они и являются общими делителями
многочленов
и
.
Их бесконечно много. Среди них выделяется
нормированный
![]() .
.
можно найти с помощью алгоритма Евклида.
Пусть даны
![]() и
и
![]() и
и
![]() .
.
Разделим на :
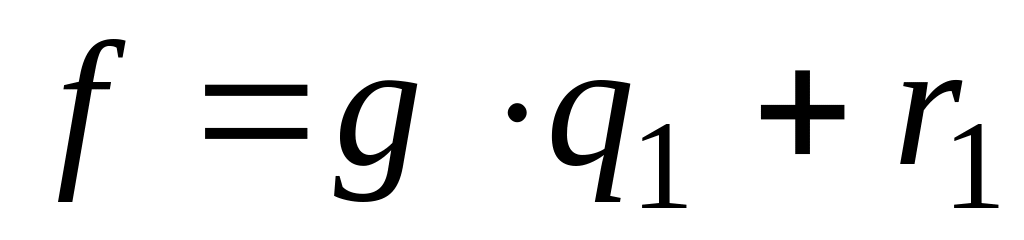 ,
,
 ,
,Если
 ,
то разделим
на
,
то разделим
на
 :
:
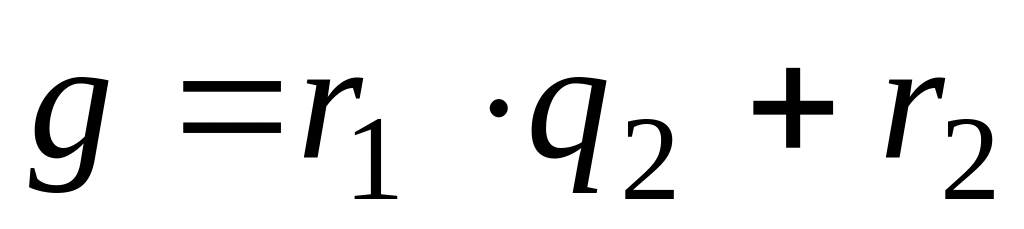 ,
,
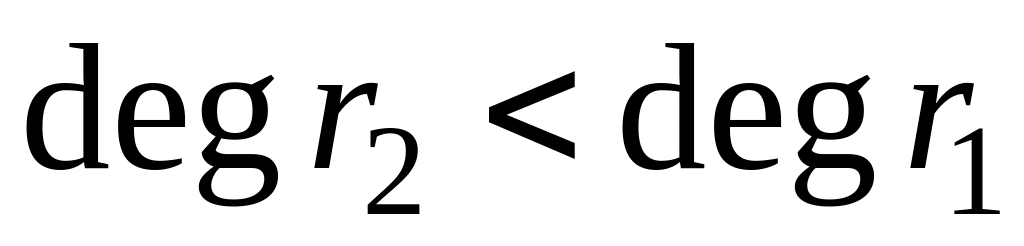 ,
,Если
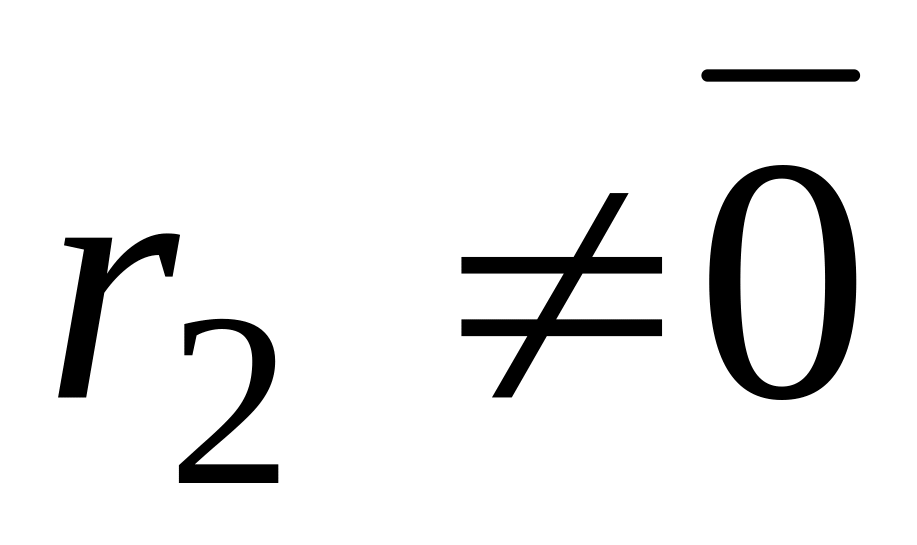 ,
то разделим
на
,
то разделим
на
 :
:
 ,
,
 ,
и т.д. до тех пор, пока в остатке не
получится
,
и т.д. до тех пор, пока в остатке не
получится
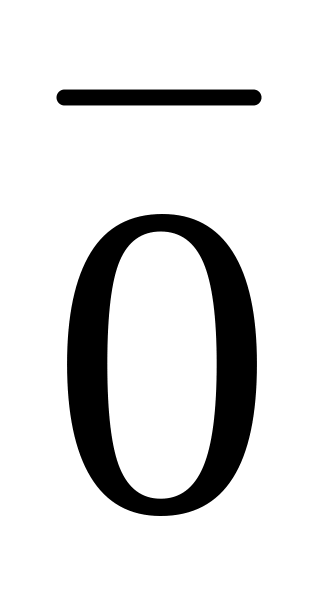 :
:
![]() ,
, ![]() ,
,
![]() .
.
![]() .
.
![]() .
.
Заметим, что деление нужно производить «уголком».
Задача 23. Найти
,
если
![]() ,
,
![]() .
.
Решение.
-
1)
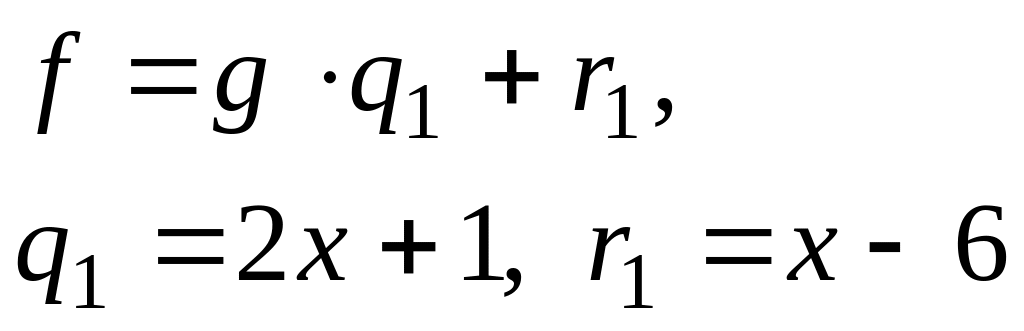


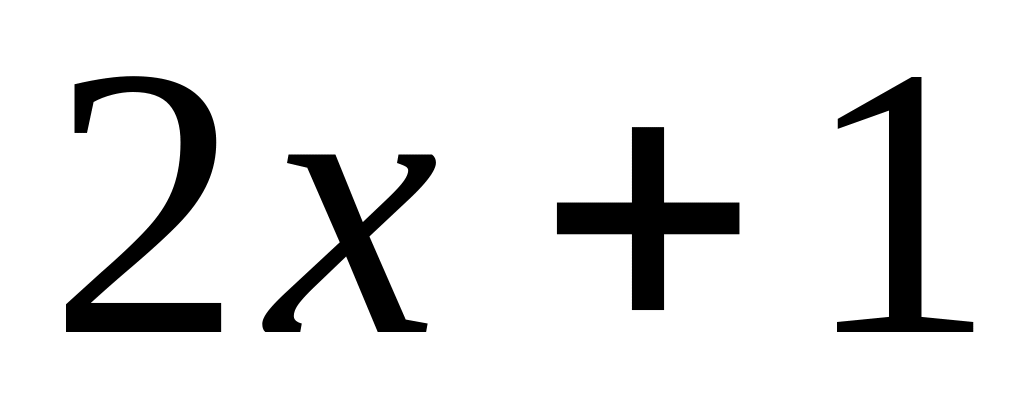
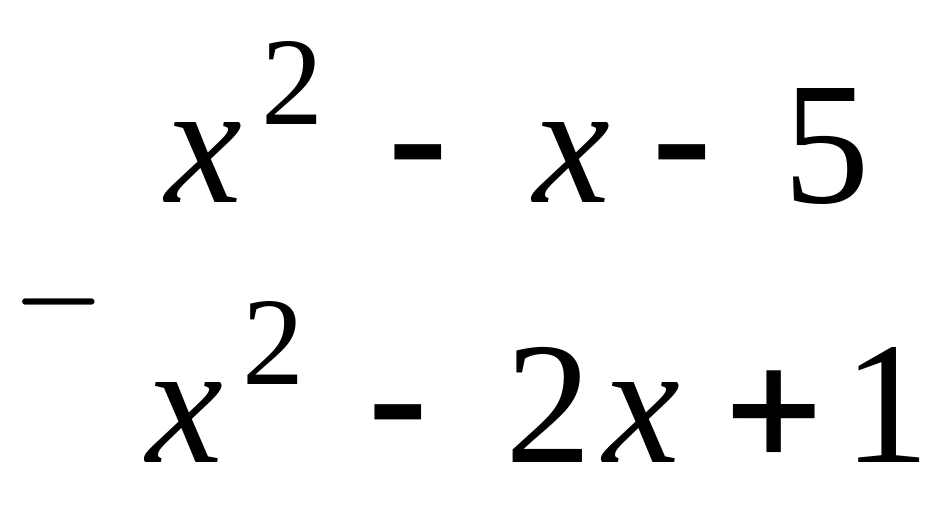

2)
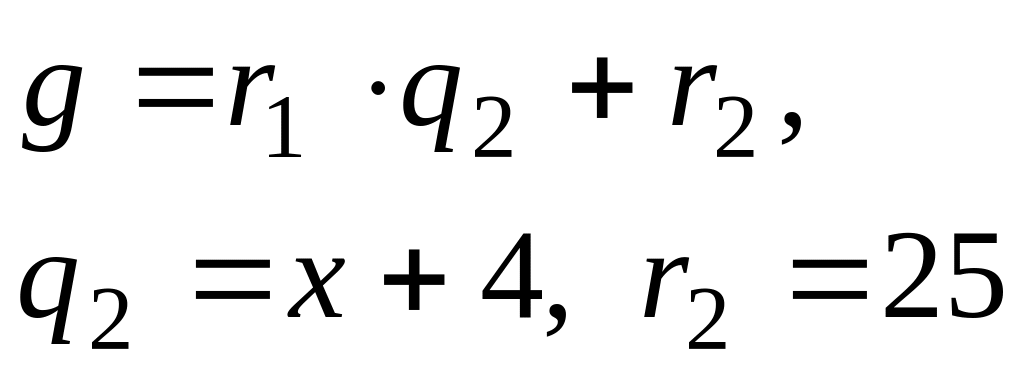
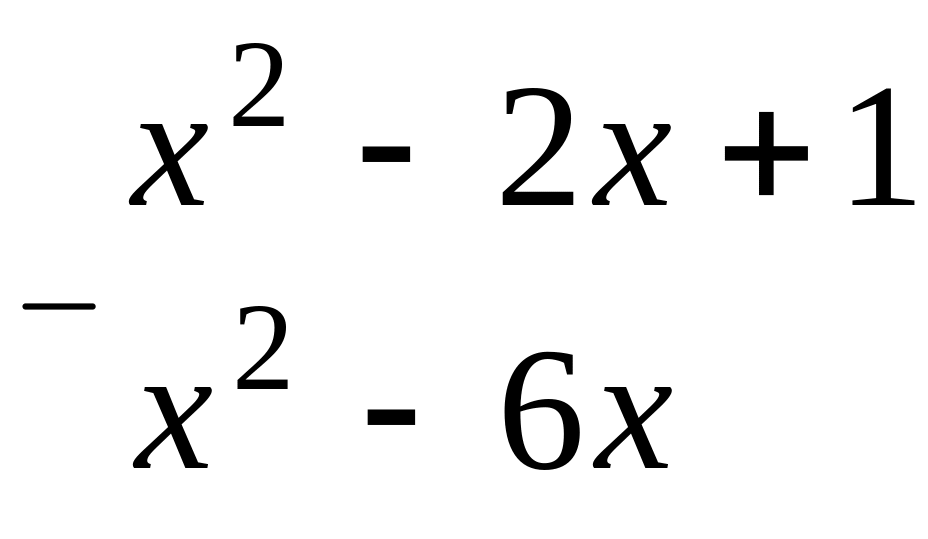
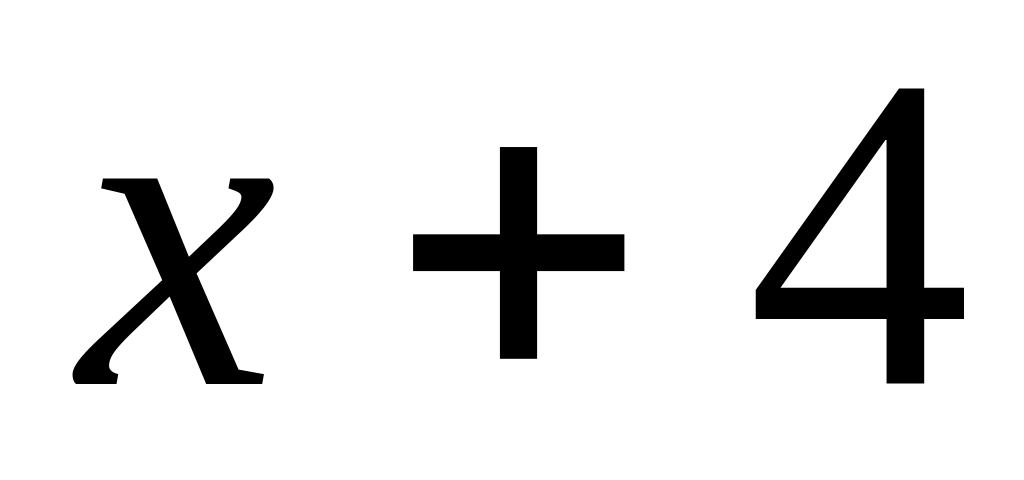
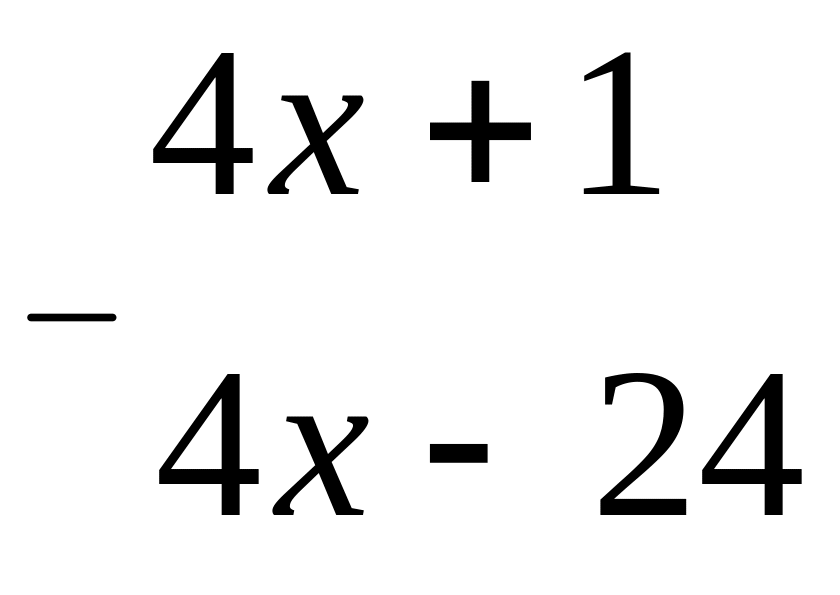
25
3)
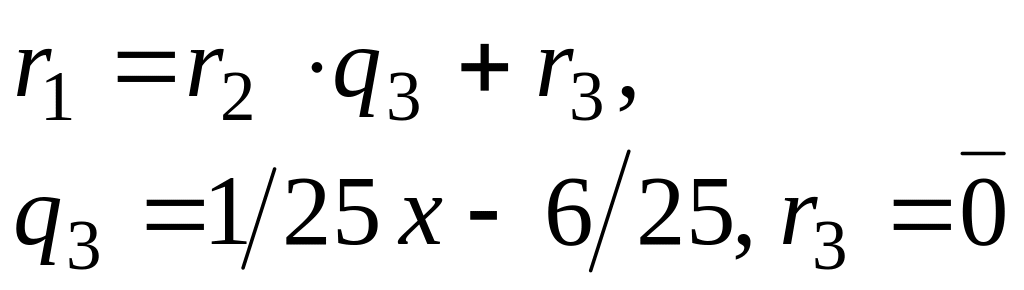
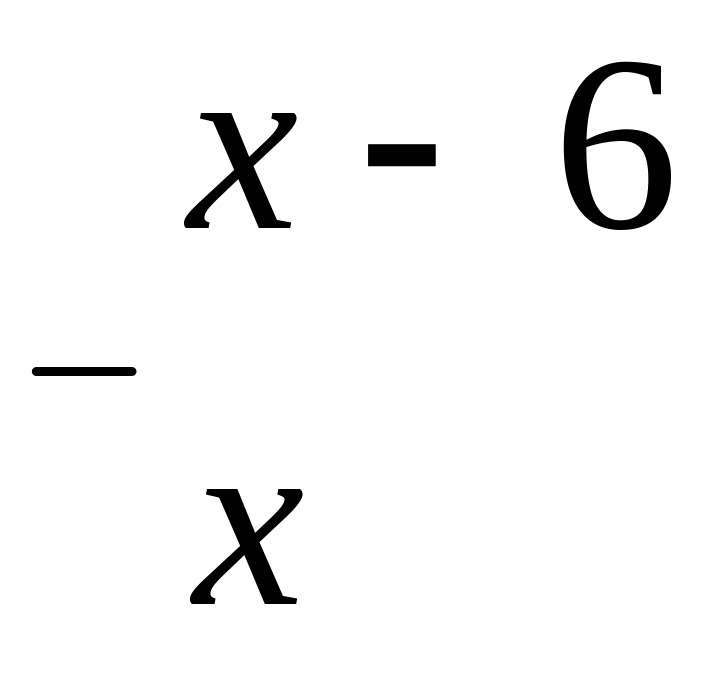
25
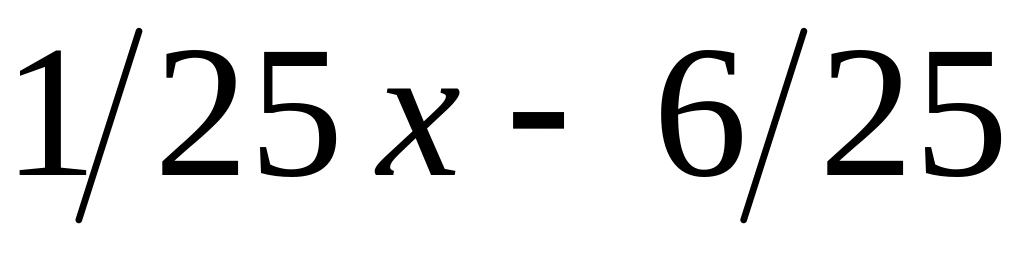
0
Значит,
![]() .
Запишем нормированный
:
.
Запишем нормированный
:
![]() .
.
С помощью алгоритма
Евклида для многочленов
и
всегда можно подобрать такие
![]() и
и
![]() ,
что
,
что
![]() .
.
Задача 24.
Для многочленов
и
подобрать такие многочлены
и
,
чтобы
![]() ,
если алгоритм Евклида для
и
состоит из двух строк.
,
если алгоритм Евклида для
и
состоит из двух строк.
Решение. Пусть алгоритм Евклида для многочленов и состоит из двух строк:
![]()
Тогда
![]() .
.
