Непараметрические методы.

Термином периодограмма (periodogram) называется оценка спектральной плотности мощности, полученная по N отсчетам одной реализации случайного процесса согласно определению (*) (естественно, не путем взятия предела, а усреднением конечного числа слагаемых). Таким образом периодограмма рассчитывается по формуле:

Деление на частоту дискретизации fg необходимо для получения оценки СПМ аналогового случайного процесса, восстановленного по отсчетам x(k).

Если при расчете спектра используется весовая функция (окно) с коэффициентами ω(k), последняя формула слегка модифицируется – вместо числа отсчетов N в знаменателе должна стоять сумма квадратов модулей коэффициентов окна. Полученная оценка СПМ называется модифицированной периодограммой (modified periodogram)

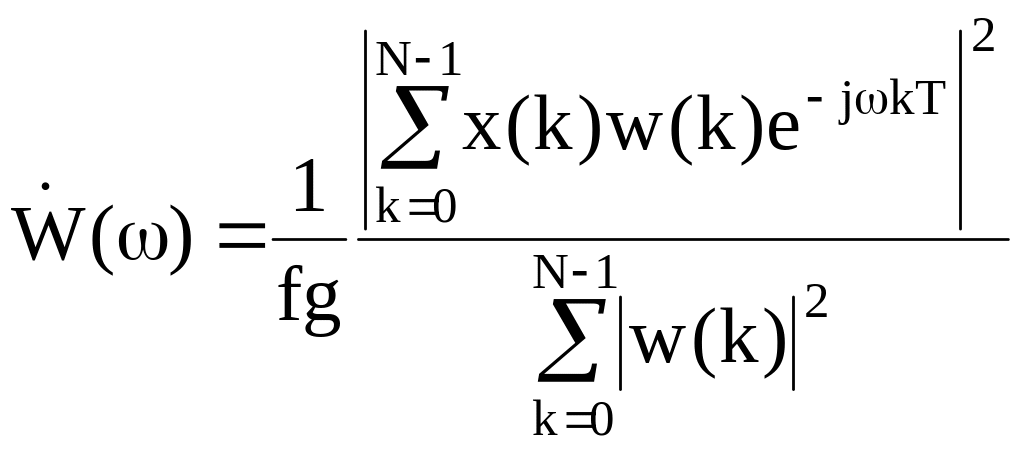
Можно показать, что периодограмма не является состоятельной оценкой СПМ, поскольку ее дисперсия сравнима с квадратом математического ожидания. С ростом числа используемых отсчетов значения периодограммы начинают все быстрее флуктуировать.

Виды периодограммы.

При вычислении периодограмм по длинному фрагменту случайного сигнала она оказывается весьма изрезанной. Для уменьшения этой изрезанности необходимо применять некоторое усреднение.

Периодограмма Даньелла (Daniell).

Даньел предложил сглаживать быстрые флуктуации выборочного спектра путем усреднения по соседним отсчетам спектра. Если для вычисления выборочного спектра на сетке частот , 0≤k≤N-1 используется ДПФ алгоритм, то оценка Даньелла получается путем усреднения в Р точках с каждой стороны от этой частоты

Периодограмма Бартлетта.

Согласно Бартлетту создается псевдоансамбль периодограмм за счет деления последовательности из N отсчетов данных на Р неперекрывающихся сегментов по D отсчетов в каждом: DP≤N. По каждому сегменту вычисляется спектральная оценка, а затем усредняется по сегментам:

Если корр. функция сигнала на длительности сегмента затухает до пренебрежимо малых значений, то периодограммы отдельных сегментов можно считать независимыми, и в этом случае дисперсия периодограммы Бартлетта обратно пропорциональна числу сегментов. Однако с ростом числа сегментов при фиксированном общем числе отсчетов сигнала падает разрешение (потому, что сегменты становятся короче).

Периодограмма Уэлча (Welch).

Уэлч внес в метод Бартлетта два усовершенствования: использование весовой функции и разделение сигнала на перекрывающиеся фрагменты. Применение весовой функции позволяет ослабить растекание спектра и уменьшить смещение получаемой оценки СПМ ценой незначительного ухудшения разрешающей способности. Перекрытие же сегментов введено для того, чтобы увеличить их число и уменьшить дисперсию оценки.

Обозначим через ΔN величину сдвига между сегментами, которая должна удовлетворять условию , где τ_k – интервал корреляции исследуемого процесса. Разобьем сигнал на сегментов. В результате мы получим Р слабо коррелированных реализаций сигнала.

Отсчеты каждого сегмента взвешиваются окном w(k) и вычисляются модифицированные периодограммы.

Алгоритм Уэлча (или метод усреднения модифицированных периодограмм – avareqed modified periodofram method) организуется следующим образом.

1. Вектор отсчетов сигнала делится на перекрывающиеся сегменты. НА практике, как правило, используется 50% перекрытия. Строго говоря, степень перекрытия оптимальная зависит от вида применяемого окна. В частности, можно показать, что для гаусовских случайных процессов при использовании окна Хана минимальная дисперсия оценки СПМ получается при перекрытии сегментов на 65%.

2. Каждый сегмент умножается на используемую весовую функцию.

3. Для взвешенных сегментов вычисляются модифтцтрованные периодограммы.

4. Периодограммы всех сегментов усредняются.

Как и в методе Бартлетта, в методе Уэлча дисперсия оценки примерно обратна числу сегментов, но так как сегментов по Уэлчу больше, дисперсия меньше.

Лекция № 8.

Весовые окна (весовые функции).

Итак периодограмма:

.

Для уменьшения растекания спектра при ДПФ применяются весовые функции (weight rug functions), которые называются окнами (windows). В случае применения окна перед расчётом ДПФ сигнал умножается на весовую функцию, которая должна спадать к краям сегмента:

.

Роль весовой функции можно рассматривать с различных точек зрения. Проанализируем ситуацию во временной области. Если мы используем весовую функцию с максимумом в середине (при ) и плавно спадает к краям ( и ), это приведёт к ослаблению скачков, и т.о. к ослаблению растекания спектра.

Аналогичный вывод можно получить и в частотной области. Умножение сигнала на весовую функцию соответствует свёртке спектров сигнала и весовой функции в частотной области. Это приводит к тому, что пики в спектре сигнала несколько расширяются, но уровень боковых лепестков снижается, что и является целью взвешивания. Т.е. мы снижаем уровень боковых лепестков АЧХ фильтров, соответствующих отдельным каналам ДПФ. Естественной платой за это является расширение центрального лепестка АЧХ. Поэтому должен существовать компромисс.

Свойства окон.

1. .

2. К своим краям окно должно спадать.

Количественные характеристики окон.

1. Коэффициент утечки (leakage factor), который показывает, какая доля общей мощности окна сосредоточена в боковых лепестках спектра окна.

2. Уровень максимального из боковых лепестков спектра относительно главного лепестка (relative side lobe attemstion).

3. Ширина главного лепестка по уровню – 3 дБ (main lobe width).

Важнейшие окна ( ).

1. Естественные окна.

1.1. Прямоугольное окно (boxcar).

1.3. Треугольное окно.

Для нечётных n.

Треугольное окно симметрично при нечётном n, крайние значения (при и ) равны , а середине окна при отсчёт окна равен 1.

При четном n окно несимметрично, его можно представить как отсчёты треугольного импульса, который начинается при и заканчивается при . Вершина импульса при , его амплитуда равна ! . При отсчёт равен 1.

Уровень первого бокового лепестка .

1.2. Окно Бартлетта. По сути тоже треугольное, но считается иначе:

При и . Независимо от чётности и нечётности окно симметрично. Максимум , поэтому при нечётном n окно Бартлетта не достигает 1 в середине. Уровень первого бокового лепестка, как и треугольного окна – 26,5 дБ.

2. Обобщенные косинусные окна.

2.1. Окна Хана.

Названо в честь австрийского метеоролога Юлиуса фон Хана (почему ?). Непр. название hanning (в предыдущем версия х Matlaba).

.

cos² или косинус на пьедестале, или приподнятый косинус.

Уровень первого бокового лепестка составляет – 31,5 дБ.

2.2. Окна Хэмминга.

.

Уровень первого бокового лепестка составляет – 43 дБ.

2.3. Окно Блэкмена.

.

Уровень первого бокового лепестка составляет – 58 дБ.

3. Специальные окна.

3.1. Окна Кайзера.

I₀ – модифицированная функция Бесселя первого рода нулевого порядка. Чем больше β, тем больше доля энергии в главном лепестке (и тем он шире), и тем меньше уровень боковых лепестков. На практике β примерно от 4 до 9.

3.2. Окно Чебышева (равноволновое).

Для него все боковые лепестки имеют одинаковый заданный при расчёте уровень. Сначала вычислим ЧХ.

.

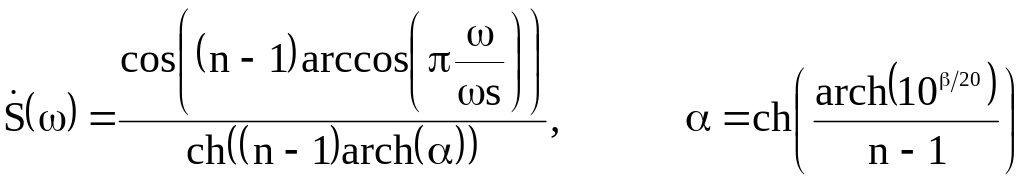Здесь β – уровень подавления боковых лепестков, n – число отсчётов окна.

Параметрические методы спектрального оценивания.

В отличие от непараметрических методов параметрические методы предполагают наличие некоторой математической модели анализируемого случайного процесса. Спектральный анализ в этом случае сводится к отысканию параемтров модели, при которых она наиболее близко соответствует реально наблюдаемому сигналу, т.е. к решению оптимизационной модели.

Модель авторегрессии – скользящего среднего.

Случайный процесс, представленный последовательностью отсчётов согласно АРСС – модели (ARMA – autoregressive moving average) формируется путём пропускания отсчётов белого шума через фильтр:

.

Всегда можно положить .

– передаточная функция некоторого фильтра.

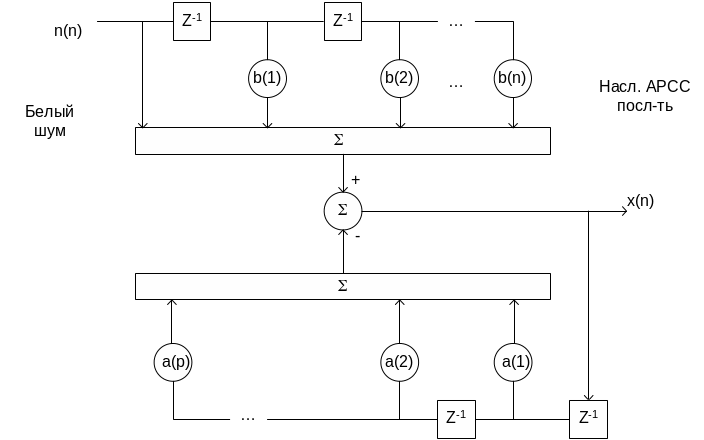
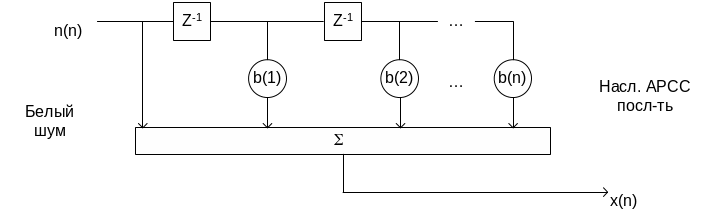
Параметры характеризуют модель СС, параметры соответствуют АР модели.

Все 3 модели могут применяться в задачах оценивания СПМ.

Обозначения АРСС (p, q), AP (p), CC (q), p и q – порядок авторегрессии и порядок СС соответственно.

Спектры АР, СС и АРСС имеют вид:

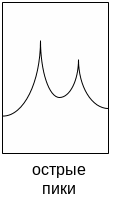
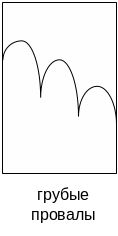
В зависимости от задачи спектрального оценивания выбирают модель. Далее у нас это будет АР-модель.

Лекция № 9.

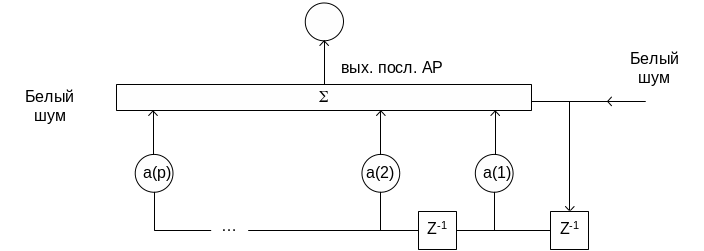
Авторегрессионная модель.

Итак, согласно авторегрессионной модели, сигнал формируется путём пропускания дискретного белого шума через рекурсивный фильтр N-го порядка.

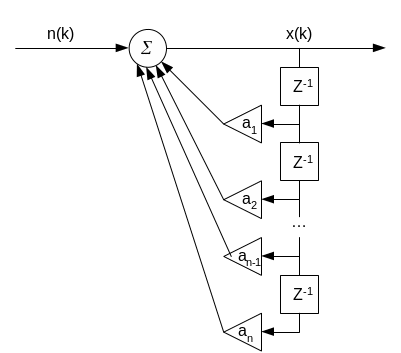
Спектральная плотность мощности такого сигнала пропорциональна квадрату модуля коэффициента передачи фильтра:

.

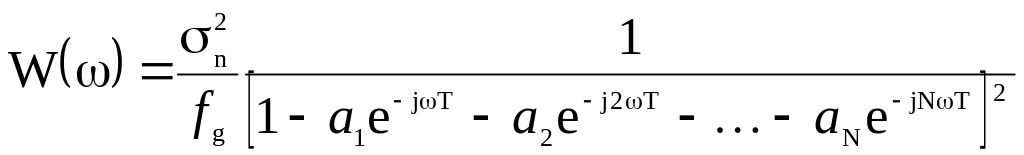Т.о. данный метод спектрального анализа сводится к определению коэффициентов модели заданного порядка N, оценка мощности белого шума и расчёту СПМ по формуле для .

Для определения коэффициентов модели производится минимизация ошибки линейного предсказания сигнала. Сущность метода состоит в следующем. Сигнал пропускается через нерекурсивный фильтр с коэффициентами .

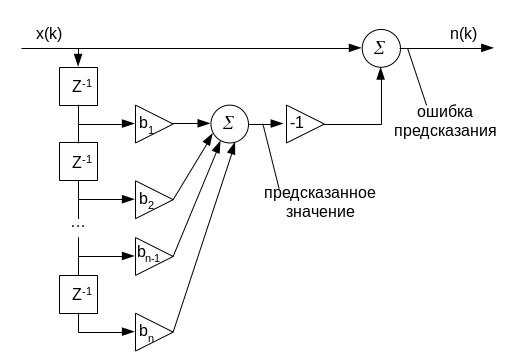
Взвешенную сумму предыдущих отсчётов сигнала называют линейным предсказанием (linear prediction) следующего входного отсчёта, а выходной сигнал фильтра, т.е. разность между истинным и предсказанным значением сигнала – ошибкой предсказания (prediction error).

Z-преобразование ошибки предсказания с учётом того, что сигнал сформирован как авторегрессия, можно записать так:

.

Отношение двух полиномов можно в общем случае записать в виде Z-преобразования бесконечной импульсной характеристики соответствующего рекурсивного фильтра , причём т.к. , первый элемент этой импульсной характеристики в данном случае равен единице.

.

Сам выходной сигнал – это результат преобразования белого шума эквивалентным фильтром :

Поскольку отсчёты белого шума независимы, дисперсия сигнала рассчитывается так:

.

Отсюда видно, что , причём равенство достигается только тогда, когда для всех i. Это возможно только в том случае, когда и совпадают.

Т.о. коэффициенты фильтра, минимизирующего дисперсию (или СКО) ошибки предсказания, совпадают с коэффициентами АР модели формирования сигнала.

Теперь разберёмся, как рассчитать коэффициенты предсказывающего фильтра по отсчётам сигнала . Ошибка предсказания:

.

Нам нужно подобрать коэффициенты так, чтобы минимизировать среднеквадратическое значение . Возведём в квадрат.

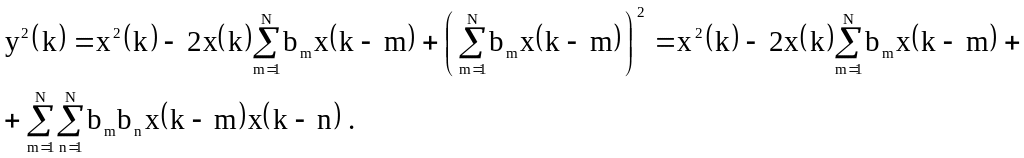Теперь нужно усреднить это по ансамблю реализаций, чтобы получить средний квадрат. Считаем, что случайный процесс центрирован, поэтому математическое ожидание равно нулю, а средний квадрат равен дисперсии.

.

Усреднённые попарные произведения, входящие в это выражение, дают значения корреляционной функции входного сигнала:

,

,

.

Тогда средний квадрат сигнала :

.

Дифференцирование выражения по даёт:

.

Т.о. для нахождения коэффициентов линейного предсказания необходимо решить систему линейных уравнений:

Можно записать эту систему в матричном виде:

,

здесь – корреляционная матрица сигнала , – столбец коэффициентов , – столбец значений корреляционной функции для k от 1 до N.

Искомое решение

.

Подстановка найденного вектора в выражение для даёт минимально возможное значение среднего квадрата ошибки предсказания:

.

На практике мы не знаем истинной корреляционной функции исследуемого сигнала, поэтому для минимизации ошибки предсказания используются оценки КФ, полученные путём временного усреднения.

Помимо спектрального анализа техники линейного предсказания широко используется для кодирования речевых сигналов. При этом звуковой сигнал делится на фрагменты (кадры) и вместо самих отсчётов звука для каждого кадра передаются только коэффициенты АР модели формирования звука. Это позволяет во много раз уменьшить требуемую скорость передачи данных. Такая технология используется, например, в сотовых телефонных сетях GSM и радиотелефонах стандарта ДЕСТ.

Итак, задача параметрического спектрального анализа распадается на два этапа: сначала необходимо получить оценку корреляционной матрицы , а затем решить систему уравнений:

.

Корреляционная матрица.

Для дискретного процесса длиной N отсчётов его корреляционная функция может быть представлена в виде матрицы, которая называется корреляционной (считаем, что процесс центрирован, т.е. его математическое ожидание равно нулю):

Черта сверху – усреднение по ансамблю реализации. Если процесс нестационарный, все элементы могут быть различными. Для стационарного процесса корреляционная матрица полностью определяется своими первыми строкой и столбцом, поскольку вдоль всех диагоналей, параллельной главной, стоят одинаковые элементы:

Оценка корреляционной матрицы.

Элементы корреляционной матрицы эргодического дискретного случайного процесса определяются как усреднённые по времени произведения сдвинутых копий бесконечно длинной реализации:

Здесь векторное обозначение использовано для бесконечного столбца отсчётов реализации случайного процесса, задержанной на m тактов, а угловые скобки обозначают усреднение по времени. Для большей общности считается, что случайный процесс может быть комплексным, поэтому вместо транспонирования к одному из векторов применена операция эрмитова сопряжения (комплексное сопряжение + транспонирование).

Однако на практике нам доступен для наблюдения только фрагмент реализации, ограниченный по времени. Из-за этого при формировании сдвинутых копий возникает проблема, связанная с нехваткой отсчётов на краях анализируемого интервала.

Пример. Пусть имеется последовательность из шести отсчётов

.

Нам необходимо оценить её корреляционную матрицу размером , т.е. при сдвигах на 0, 1 и 2 отсчёта. Для этого по определению придётся сформировать три вектора .

Если выписать друг под другом сдвинутые копии последовательности для требуемых сдвигов, то видим, что для некоторых отсчётов сдвинутых пар нет.

Данную проблему решают несколькими методами.

1. Автокорреляционный (autocorrelation) метод. Недостающие отсчёты в начале и в конце сигнала считают равными нулю.

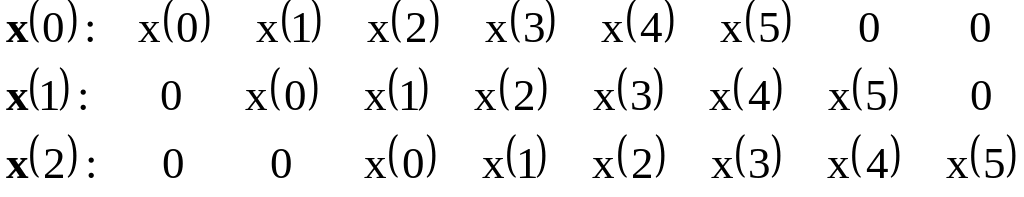
При усреднении по времени для нормировки используется длина исходной реализации (в нашем случае это 6).

;

.

Этот метод всегда даёт теплицеву матрицу.

2. Метод предзвешивания (prewindowing). Недостающие отсчёты в начале сигнала считаются равными нулю, а в конце сигнал обрезается, чтобы при всех сдвигах отсчётов хватало.

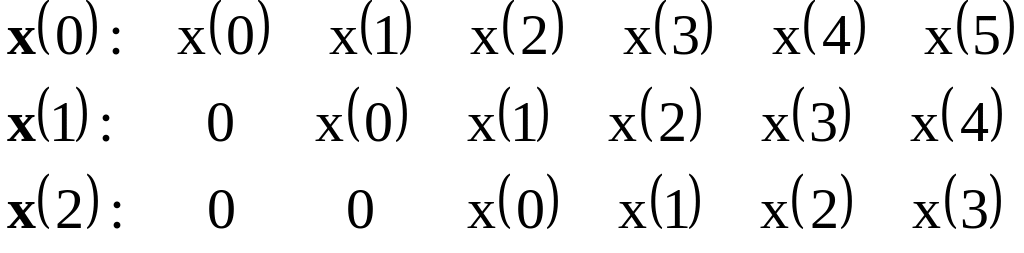
При усреднении по времени для нормировки используется длина исходной реализации (в нашем случае 6). Оценка не является тепляпцевой.

;

;

;

;

;

.

Матрицы, обладающие этим свойством, называются матрицами Тёплица (Toeplitz matrix).

В случае вещественного случайного процесса и корреляционная матрица становится симметричной:

Важное свойство корреляционной матрицы действительного случайного процесса есть её неотрицательная определённость (т.е. все их собственные числа вещественны и неотрицательны).

3. Метод поствзвешивания (post windowing). Недостающие отсчёты в конце сигнала считаются равными нулю, в начале сигнал обрезается, чтобы при всех сдвигах отсчётов хватало.

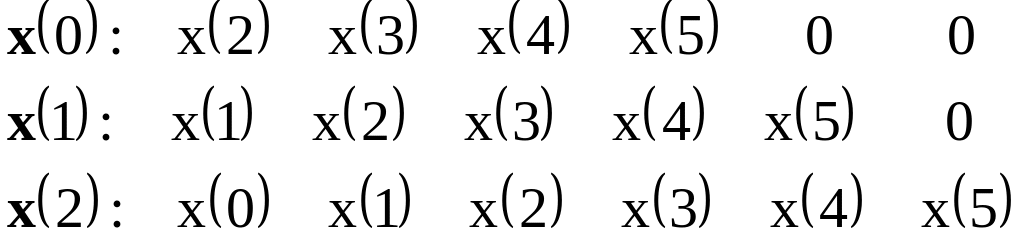
Нормировка – длина исходной реализации (6). Оценка не является теплицевой матрицей.

;

;

;

;

;

.

4. Ковариационный (covariance) метод. Сигнал обрезается в начале и в конце, чтобы всех отсчётов хватало.

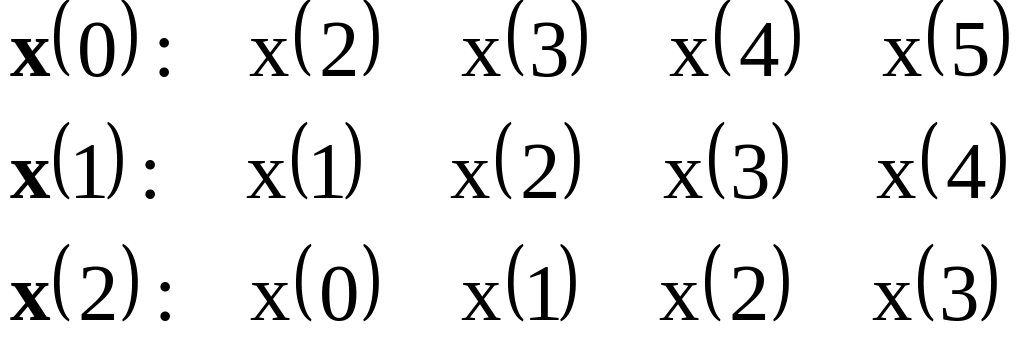
При усреднении используется длина обрезанной реализации (для примера это 4). Оценка не является теплицевой матрицей.

;

;

;

;

;

.

5. Модифицированный ковариационный метод (modified covariance). Сигнал обрезается в начале и в конце, а затем полученная матрица отсчётов расширяется: к ней добавляется её комплексно сопряжённая копия, зеркально перевёрнутая вдоль координаты временных сдвигов:

При усреднении по времени используется длина расширенной реализации (т.е. 8). Полученная оценка не является теплицевой.

;

;

.

Лекция №10.

Алгоритм Левинсона-Дарбина.

В общем случае система может решаться обычными методами решения систем линейных уравнений. Однако если корреляционная матрица имеет теплицеву структуру (это имеет место, если используется аналитически рассчитанная матрица стационарного случайного процесса, либо её оценка, рассчитанная автокорреляционным методов), можно сократить число вычислений, воспользовавшись алгоритмом Левинсона-Дарбина (Levinson-Darbin algorithm).

Перепишем систему уравнений Юла-Уокера, раскрыв в ней структуру матрицы и вектора :

При такой форме записи становится наглядно видно, что, помимо уже отмеченной теплицевой структуры матрицы, данная система обладает еще одной особенностью. Вектор-столбец правой части составлен из тех же значений корреляционной функции, которые формируют матрицу системы. Исключение составляет лишь последний элемент , отсутствующий в корреляционной матрице.

Сущность алгоритма Левинсона-Дарбина состоит в итерационном решении данной системы с постепенным увеличением её порядка. В процессе решения мы получаем решение системы для порядка предсказания равного 1, 2, 3,…,N. Таким образом, при переходе и следующей итерации необходимо выполнить две задачи:

- рассчитать значение нового коэффициента предсказания,

- обновить значения уже имеющихся.

Введём следующие обозначения:

- – корреляционная матрица размером :

;

– вектор-столбец значений корреляционной функции (правая часть порядка k):

;

– перевернутый вектор-столбец порядка k значений корреляционной функции:

,

– вектор-столбец коэффициентов предсказания k-ого порядка, полученный на k-й итерации (в данном случае нижний индекс показывает размер вектора, а верхний индекс в скобках – номер итерации):

;

где – i-й элемент вектора коэффициентов предсказания, полученного на k-й итерации (для скалярных величин нижний индекс обозначает номер элемента вектора);

– перевёрнутый вектор-столбец коэффициентов предсказания k-ого порядка, полученный на k-й итерации:

,

– вектор-столбец коэффициент предсказания k-ого порядка, обновлённый в результате выполнения ( )-й итерации;

– средний квадрат ошибки предсказания при использовании предсказывающего фильтра k-ого порядка.

Итак, сначала рассматриваем предсказание первого порядка. В этом случае в системе остаётся лишь одно уравнение:

.

Уравнение имеет очевидно решение:

.

(в данном случае вектор коэффициентов предсказания вырождается в скаляр).

Теперь предположение, что нам известно решение системы Юла-Уокера для некоторого порядка k, то есть в нашем распоряжении имеется вектор , для которого

(*)

Кроме того, сразу же заметим, что благодаря теплицевой структуре корреляционной матрицы данное равенство не нарушается при вертикальном повороте вектор-столбцов и :

.

Наша задача состоит в том, чтобы выразить решение для ( )-й итерации , через уже имеющееся решение . Для этого нужно решить систему уравнений:

.

Прежде всего заметим, что по сравнению с предыдущей итерацией (*) к корреляционной матрице добавились новые строка и столбец, а к корреляционному вектору – новый элемент . Покажем это в явном виде, переписав последнюю формулу таким образом:

.

Выполнив в этой формуле блоковое умножение матриц, получаем систему из двух уравнений:

Подставим в первое уравнение этой системы выражение для и для :

.

Если матрица невырождена, имеем:

.

Т.о. образом мы выразили первые k элементов нового вектора коэффициентов предсказания через их старые значения, полученные на предыдущей итерации ( ). Но ещё не рассчитан элемент нового вектора . Подставим последнее уравнение во второе уравнение системы:

.

Это скалярное уравнение , решение которого находится элементарно:

(**)

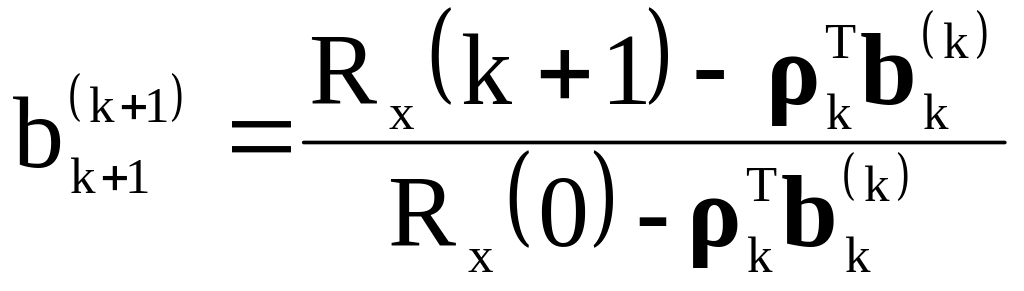Выполнив вычисления по последней формуле, а затем по предпоследней, можно получить окончательное значения нового вектора коэффициентов предсказания:

(***)

Дополнительно упростить расчёты можно, вычисляя знаменатель формулы (**) рекурсивно. Этот знаменатель равен среднему квадрату ошибки предсказания. Действительно,

.

Выразим через – средний квадрат ошибки предсказания, полученный на предыдущей итерации. Для этого выделим в векторе добавляемый элемент, а вектор представим в виде (***):

Подставим сюда и выполним умножение строки на столбец:

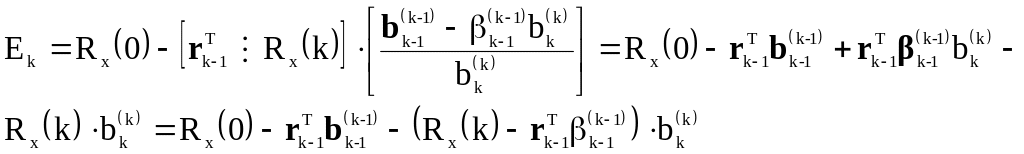
В получившемся выражении первые два слагаемых дают – средний квадрат ошибки, полученный на предыдущий итерации:

,

выражение в скобках равно:

.

Окончательно имеем рекурсивное выражение:

.

Итак, укажем последовательность операций для выполнения алгоритма Левинсона-Дарбина.

Инициализация. Вычисляются параметры предсказания первого порядка и средний квадрат ошибки предсказания :

, .

Рекурсия. Для выполняются следующие действия:

– вычисляется добавляемый элемент вектора коэффициентов предсказания:

,

– производится обновление остальных коэффициентов предсказания:

,

– пересчитывается средний квадрат ошибки предсказания:

.

Спектральные свойства матриц.

Вы знаете, что для линейной системы собственных функцией является комплексная экспонента . Линейная система оставляет неизменной форму экспоненциального сигнала, поданного на её вход, изменяя лишь его комплексную амплитуду. (Решение линейного уравнения есть разложение по собственным функциям).

Аналогично, если ненулевой вектор в результате линейного преобразования, описываемого квадратной матрицей остаётся неизменным и лишь изменяет свой масштаб в раз, т.е.:

. .

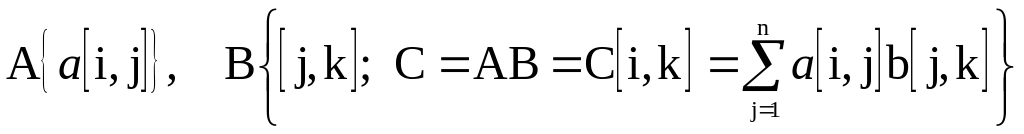
то говорят, что он является собственным вектором матрицы . Скаляр, соответствующий этому собственному вектору, называется собственным значением.

Полином порядка называется характеристическим полиномом матрицы .

Определитель

– вычеркиваем 1 строки, j столбца. Скаляр.

корней уравнения порождают собственных значений :

.

Собственные значения и собственные векторы вместе образуют собственную систему матрицы . Множество собственных значений в математике принято называть спектром матрицы . (Не путать со спектром сигнала!).

Определяя след матрицы как сумму элементов главной диагонали:

,

можно показать, что

.

Главными собственными векторами называются собственные векторы, соответствующие наибольшему по величине собственными значению матрицы .

Если матрица эрмитова, то её можно разложить по собственным векторам и собственным значениям:

.

(Эрмитова, если квадратный полином матрицы , обладающая свойством полиномного сопротивления симметрии ).

Последнее выражение в математике называется спектральным представлением (или спектральным различием) матрицы . (Не путать со спектром различием сигнала).

Эрмитова матрица может быть представлена с помощью унитарной матрицы , состоит из собственных векторов и диагонали матрицы, содержащей собственные значения.

Метод MUSIC.

Метод MUSIC (MUltiple SIgnal Classification) предназначен для спектрального анализа сигналов, представляющих собой сумму нескольких синусоид (в общем случае – нескольких комплексных экспонент) с белым шумом. Целью спектрального анализа подобных сигналов, как правило, является не расчёт спектра как такового, а определение частот и уровней (амплитуд и мощностей) гармонических составляющих. Метод MUSIC предназначен именно для этого, поэтому получаемая с его помощью зависимости уровня сигнала от частоты называется псевдоспектром (pseudo spectrum).

В основе метода лежит анализ собственных чисел и собственных вектором корреляционной матрицы сигнала. Мы рассмотрим основные идеи.

Итак, пусть сигнал представляет собой сумму M комплексных экспонент, начальные фазы которых случайны, с белым шумом:

.

– отсчёты белого шума;

– амплитуда, частоты и начальные фазы комплексной экспоненты, содержащейся в сигнале, Т – период дискретизации.

– равномерно распределены в интервале .

Корреляционная функция такого сигнала будет иметь вид:

.

единичная ими функция

– дисперсия шума .

Далее из отсчётов корреляционной функции формируется корреляционной матрицы размера , причём размер матрицы должен превышать число комплексных экспонент .

Анализируя собственные числа и собственные вектора такой корреляционной матрицы, можно показать, что наименьшее собственное число равно , и оно имеет кратность , а остальные M собственных чисел превышают , а их конкретные значения зависят от амплитуд и частот комплексных экспонент.

Собственные векторы, соответствующие M наибольшим собственным числам представляют собой линейные комбинации комплексных экспонент, содержащихся в сигнале. Множество всех таких линейных комбинаций называется сигнальным подпространством (signal subspace), а упомянутые векторы образуют базис в этом подпространстве.

Оставшиеся собственных векторов ортогональны всем комплексным экспонентам, содержащимся в сигнале. Эти векторы образуют базис шумового подпространства (noise subspace).

Спектр комплексной экспоненты, рассчитанный аналитически, представляет собой дельта-функцию, расположена на собственной частоте. Чтобы получить бесконечные выбросы на частотах , псевдоспектр по методу MUSIC рассчитывается следующим образом:

.

Здесь – n-ый элемент k-ого собственного вектора корреляционной матрицы. Векторы пронумерованы по убыванию соответствующих им собственных чисел.

Таким образом, внешняя сумма по k от до N задаёт участие в вычислениях только шумовых собственных векторов. Внутренняя сумма представляет собой вычисления спектра собственного вектора на частоте . Шумовые собственные векторы ортогональны всем комплексным экспонентам с частотами , содержащимся в сигнале. Поэтому при все внутренние суммы стремятся к нулю, т.е. . Сами частоты можно получить, приравняв к нулю знаменатель:

.

Раскроем квадрат модуля:

.

Теперь видно, что левая часть полученного выражения в конечном счёте представляет собой полином относительно степени . Те корни этого полинома, которые лежат на единичной окружности, равны и для расчёта их частот остаётся вычислить аргументы этих комплексных чисел и разделить их на T.

Всё сказанное относится к идеализированной модели сигнала и аналитически полученной корреляционной функции. В реальных ситуациях, когда сигнал не вполне соответствует модели ( ), а его корреляционная матрица оценивается по результатам наблюдений (к тому же зачастую без возможности усреднения по нескольким наблюдениям), результаты оказываются несколько иными: пики в ( ) имеют конечную высоту, а корни полинома не строго лежат на единичной окружности. Однако, если сигнал близок к модели, метод MUSIC даёт хорошие результаты.

Метод EV.

Метод анализа собственных векторов (eigenvectors, EV) является близким родственником метода MUSIC. Его отличие состоит в том, что в 2-х последних формулах при суммировании по k используются весовые коэффициенты, обратно пропорциональные соответствующим собственным числам. Т.о.

,

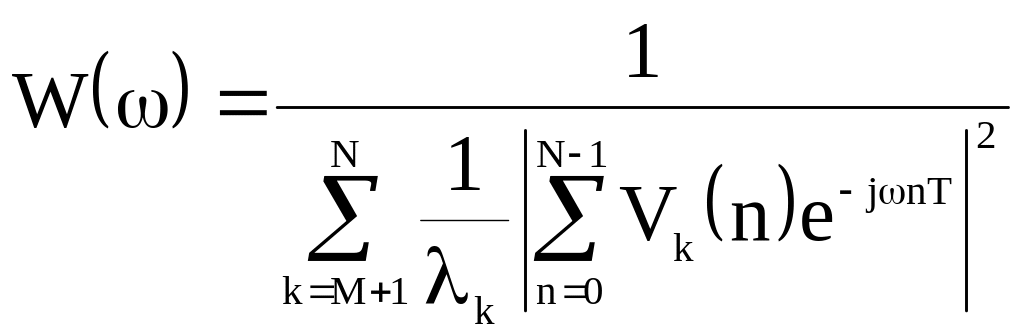и уравнение для отыскания собственных частот

.

Здесь – собственное число, соответствующее k-му собственному вектору .

При заданном значении M метод EV порождает меньше ложных спектральных пиков, чем MUSIC, и, как правило, лучше передаёт форму спектра шума.

Ещё раз подчеркнём, что MUSIC и EV не СПМ, а псевдо спектры, позволяющие получить оценки гармонических составляющих с разрешением, более высоким, чем АР модели.

Лекция №11

Цифровая фильтрация.

Одной из наиболее часто решаемых задач в практике обработки сигналов является их фильтрация. Фильтр – это система, пропускающая сигналы в полосе частот и подавляющая сигналы остальных частот.

Различают такие фильтры (по видам):

- фильтры НЧ (ФНЧ, Cow-pass filter), пропускающие частоты ниже некоторой частоты среда ω₀,

- фильтры ВЧ (ФВЧ, high-pass filter), пропускающие частоты большие некоторой частоты среда ω₀,

- полосовые фильтры (ПФ, band-pass filter), пропускающие частоты в некоторой полосе (ω₁…ω₂), они могут также характеризоваться средней частотой ω₀ = (ω₁ + ω₂)/2 и шириной полосы пропускания Δω = ω₂ – ω₁,

- режекторные фильтры (заграждающий фильтр, фильтр-пробка, полосно-задерживающий фильтр, band-stop filter), пропускающий на выход все частоты, кроме лежащих в некотором диапазоне ω₁…ω₂ (они тоже могут характеризоваться средней частотой ω₀ = (ω₁ +ω₂)/2 и шириной полосы задерживания.

Идеальная форма АЧХ таких фильтров.

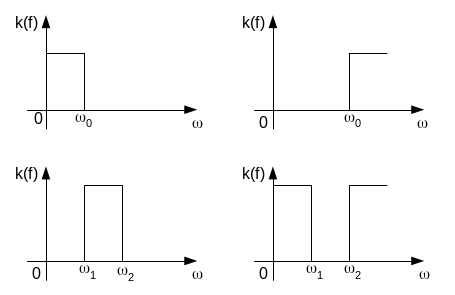
Однако такая идеальная прямоугольная форма АЧХ физически нереализуема. Поэтому в теории аналоговых фильтров разработан ряд методов аппроксимации прямоугольных АЧХ. Это мы рассмотрим позже.

Кроме того, рассчитав ФНЧ, его можно несложными преобразованиями превратить в ФВЧ, ПФ или РФ. Поэтому расчет аналогового фильтра начинается с расчета так называемого фильтра-прототипа, представляющего собой ФНЧ с частотой среза ω₀, равной 1 рад/с. Функции преобразования мы рассмотрим ниже.

Для разных фильтров частота среза ω₀ определяется по разному. Немного забегая вперед, скажем, что для фильтра Баттерворта частота среза определяется по уровню , для фильтра Чебышева 1-го рода и эллиптического фильтра – по уровню пульсаций в полосе пропускания, для Чебышева 2-го рода – по уровню пульсаций в полосе задерживания. Наконец, для фильтров Бесселя само понятие частоты среза является весьма условным.

1. Фильтр Баттервотра.

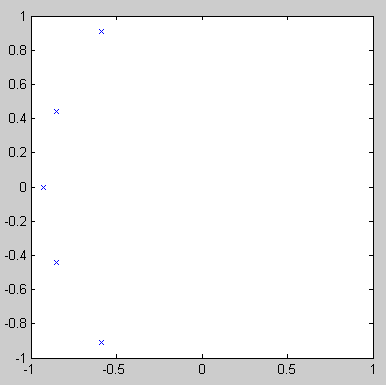
Функция передачи фильтра-прототипа Баттерворта (Butterworth filer) не имеет нулей, а ее полюсы равномерно расположены на s-плоскости в левой половине окружности единичного радиуса.

Благодаря такому расположению полюсов формула АЧХ фильтра Баттерворта очень проста:

ω₀ – частота среза (для фильтров-прототипов 1 рад/с), n – порядок фильтра.

Коэффициент передачи на нулевой частоте 1, на частоте среза независимо от порядка фильтра = 0,707 = -3 дБ. При ω → ∞ АЧХ → 0.

АЧХ фильтра Баттерворта является максимально плоской при ω → 0 и ω → ∞. Это означает, что в данных точках равны нулю 2n-1 производных АЧХ по частоте.

В целом АЧХ монотонно спадает от ω до нуля при изменении частоты от нуля до ∞.

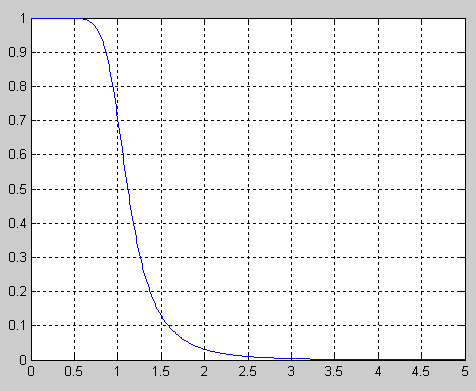
2. Фильтр Чебышева первого рода.

Функция передачи ФЧПР (Chebyshev type I filter) также не имеет нулей, а полосы е расположены в левой половине эллипса на s-плоскости.

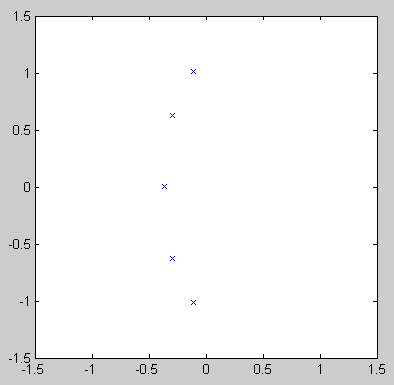
АЧХ фильтра Чебышева I р. описывается следующим образом:

где ω₀ – частота среза, T_n(x) – полином Чебышева n-го порядка, n – порядок фильтра, ε – параметр, определяющий величину пульсации АЧХ в полосе пропускания.

Полином Чебышева T_n(x) при |x| ≤ 1 колеблется в диапазоне -1, …, 1, а при |x| > 1 неограниченно возрастает по абсолютной величине. Поэтому АЧХ фильтра Чебышева ПР в полосе пропускания (при |ω|<ω₀) колеблется между значениями и 1, а вне полосы пропускания (|ω|>ω₀) монотонно затухает до нуля.

Коэффициент передачи на нулевой частоте равен 1 при нечетном порядке фильтра и - при нечетном. На частоте среза , т.е. уровню пульсаций в полосе пропускания. При ω → ∞ АЧХ → 0.

По сравнению с фильтром Баттерворта того же порядка фильтр Чебышева обеспечивает более крутой спад АЧХ в области перехода от полосы пропускания к полосе задерживания.

Значение параметра ε и уровень пульсаций R_p (в дБ) связаны следующим образом:

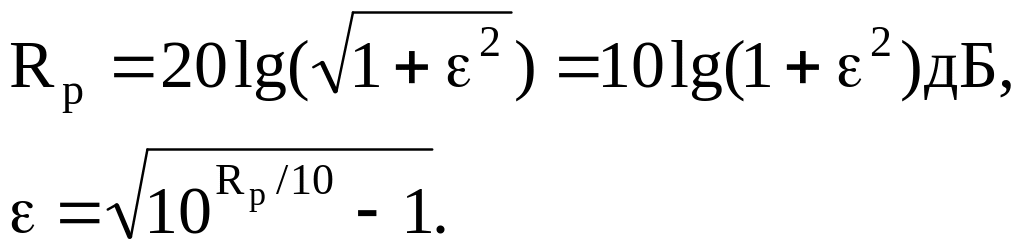
При ω → ∞ АЧХ фильтра Чебышева является максимально плоской.

3. Фильтр Чебышева второго порядка.

Функция передачи ФЧПР (Chebyshev type II filter) в отличие от предыдущих случаев имеет и нули, и полюсы.

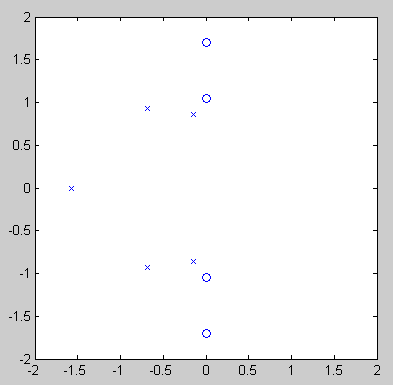
Она связана с функцией передачи фильтра Чебышева первого рода следующим образом:

Полюсы функции передачи фильтров-прототипов Чебышева П и ВР (p_1i и p_2i соответственно) связаны друг с другом соотношением:

По этой причине ФЧВР называют еще инверсными фильтрами Чебышева (inverse Ghebyshev filter). АЧХ ФЧВР описывается следующим образом:

где ε – параметр, определяющий величину пульсации в полосе задржмвания.

В результате указанного выше преобразования H(s) АЧХ ФЧВР ведет себя следующим образом: в полосе пропускания она монотонно затухает, а в полосе задерживания колеблется между нулем и .

Частотой среза фильтра Чебышева второго рода считается не конец полосы пропускания, а начало полосы задерживания.

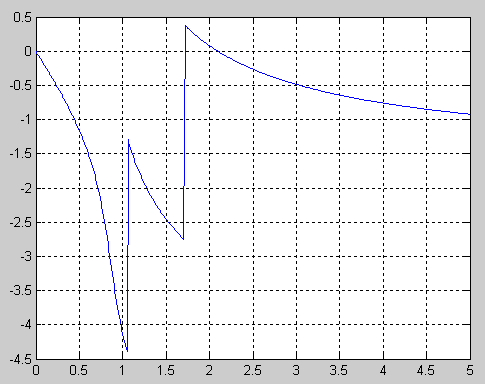
Коэффициент передачи фильтра на нулевой частоте равен 1, на частоте среза – заданному уровню пульсаций в полосе задерживания. При ω → ∞ коэффициент передачи = 0 при нечетном порядке фильтра и уровню пульсаций при четном.

Параметр ε и уровень пульсаций R_s (дБ) связаны следующим образом:

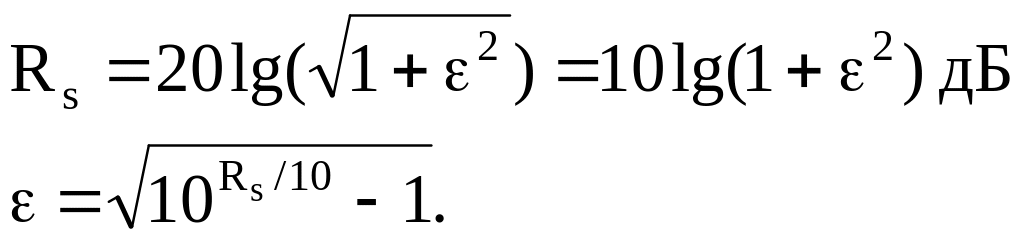
При ω = 0 АЧХ ФЧВР является максимально плоской.

4. Эллиптический фильтр.

Эллиптические фильтры (фильтр Кауэра, elliptic filter, Cauer filter) в некотором смысле объединяет свойства фильтров Чебышева I и II рода, поскольку АЧХ эллиптического фильтра имеет пульсации заданной величины, как в полосе пропускания, так и в полосе задерживания. За счет этого удается обеспечить максимально крутизну ската АЧХ.

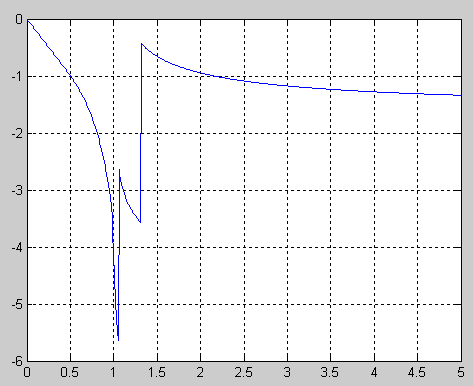
Функция передачи эллиптического фильтра имеет как полюсы, так и нули. Нули чисто мнимые и образуют комплексно-сопряженные пары.

Количество нулей функции передачи равно максимальнлму четному числу, не превосходящему порядок фильтра.

АЧХ эллиптического фильтра описывается формулой:

ω₀ – частота среза, n – порядок фильтра, R_n(…) – рациональная функция Чебышева n-го порядка, ε и L – параметры, определяющие величину пульсаций в полосе пропускания и задерживания.

5. Фильтр Бесселя.

В отличие от предыдущих типов фильтров, фильтры Бесселя (Bessel filter) не аппроксимируют прямоугольную АЧХ – их АЧХ по форме близка к гауссовой кривой (точнее, стремиться к ней с ростом порядка фильтра).

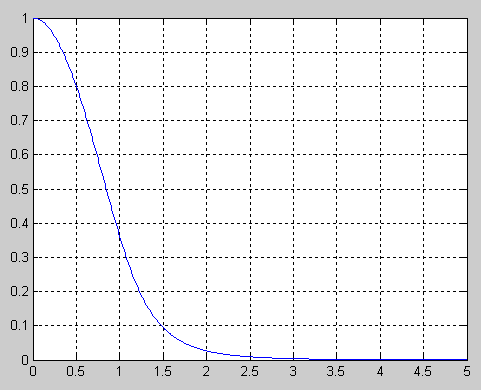
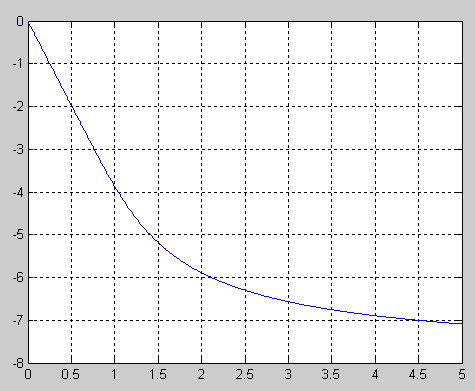
Практическая ценность ФБ определяется тем, что для них зависимость группового времени задержки от частоты является максимально гладкой в тоже ω = 0 и групповая задержка очень мало меняется в полосе пропускания.

Функция передачи ФБ имеет только полюсы, лежащие на окружности с центром в положительной области вещественной оси.