Лекция 8. Проективная геометрия

Основная идея этой чистой геометрии родилась из желания художников Возрождения создать «зрительную геометрию». Как выглядят предметы в действительности и как их можно изобразить в плоскости чертежа

С.Г. Гульд

П

Все проблемы Перспективы можно прояснить при помощи пяти терминов Математики: точка, линия, угол, поверхность и тело Леонардо да Винчи

роективная геометрия является одним из самых красивых разделов геометрии. Она резко отличается от евклидовой геометрии, где все необходимо строго доказывать, причем, некоторые доказательства весьма сложны, в ней не используются понятия параллельности, перпендикулярности и равенства отрезков и углов, и предполагается, что любые две прямые на плоскости имеют общую точку. В проективной геометрии ненужная информация отбрасывается, и в результате доказательство проходит просто и легко. К тому же она возникла в первую очередь, как практический предмет. Потребность в построении изображений по законам геометрии (проекционных чертежей), возникла именно из практических задач строительства сооружений, укреплений, пирамид и т.д., а на позднем этапе - из запросов машиностроения и техники. В связи с развернувшимся строительством различных сооружений возродилось и расширилось применение употреблявшихся в античном мире элементов проекционных изображений. Это поставило художников и архитекторов перед необходимостью начать разработку учения о живописной перспективе на геометрической основе. В эпоху Возрождения к проективной геометрии обратились живописцы, пытавшиеся изображать на плоскости объемные предметы именно так, как их видит глаз человека.

Хотя проективная геометрия возникла первоначально как один из разделов евклидовой геометрии, но позже математики поняли, что она является самостоятельным предметом, и даже больше – все остальные известные геометрии сводятся к ней. Английский математик А.Кэли сформулировал свое отношение к проективной геометрии так: «проективная геометрия – это вся геометрия». Именно поэтому практическая ценность проективной геометрии не только в ее применении для нужд архитекторов, фотографов, а в том, влиянии, которое она оказывает на другие области математики.

Проективная геометрия применяется в дизайнерском деле, в разнообразных фантастических проектах ведущих мировых архитекторов.

П роективная геометрия удивительна, она изобилует невозможностями: параллельные прямые в ней пересекаются, все параллельные прямые имеют одну общую точку, параллельные плоскости также пересекаются – по прямой. Если в ней что-то надо доказать, то это делается достаточно легко и обычно просто. Ведь если художник хочет нарисовать картину, разве будет он что-то усложнять и доказывать, его цель – нарисовать и, по возможности, как можно более правдоподобно.

Понселе

Как и все другие геометрии, проективная строго задается системой аксиом. В ней фигурируют два типа объектов, называемых «точками» и «прямыми». Между этими объектами есть некоторые отношения, схожие с точками и прямыми евклидовой плоскости, и для них выполняется ряд свойств, отличающихся от присущих евклидовым.

Возникновение проективной геометрии связано с именем известного французского математика Понселе. Он выделил как объект её изучения особые свойства геометрических фигур, которые были названы проективными. Но какие именно свойства относятся к проективным? Нарисуем произвольный куб, воображаемый или стоящий перед вами. Рисунок каждого будет отличаться, и зависеть от места, занимаемого каждым по отношению к кубу. Да и сам рисунок будет во многом отличаться от реального куба. Например, известно, что у куба все углы прямые.

На рисунке это сделать достаточно затруднительно. Не будет сохранено даже соотношение длин. Но, тем не менее, некоторые факты, касающиеся заданного куба, останутся неизменными и на этом рисунке. Так, например, прямая не превратится ни в кривую, не в окружность – она останется прямой. Изображение точки есть точка. Если некоторая точка принадлежала прямой, то и на чертеже она будет принадлежать той же прямой. Однако уже свойство точки лежать между двумя другими не сохранится. Вот сохраняющиеся свойства и называются проективными. Именно ими и занимается проективная геометрия, остальные, изменяющиеся свойства, она игнорирует.

З начительное место в проективной геометрии занимает введение так называемых несобственных (или бесконечно удаленных) геометрических элементов. Введение этих элементов – заслуга другого математика, француза Жерара Дезарга.

О

Понселе

Дезарг

н предложил добавить к обычным конечным точкам плоскости еще дополнительные, так называемые бесконечно удаленные точки, в которых пересекаются параллельные прямые. Бесконечно удаленные точки называли несобственными, или идеальными, чтобы подчеркнуть их отличие от настоящих точек. Но дальше Дезарг призывал забыть как можно быстрее об этом различии, иначе пользы от новых точек уже не будет.

Он считал, что все параллельные прямые пересекаются в точке, которая является таким бесконечно удаленным элементом. Этим шагом Дезарг положил начало проективному представлению пространства (полное проективное пространство) и сделал возможным изучение проективных преобразований.

Следуя за Дезаргом, дополним пространство Е₃ новыми точками, а именно: ко всем обычным точкам каждой прямой мысленно добавим ещё одну, несобственную точку. Будем считать, что две параллельные прямые имеют одну и ту же несобственную точку, а непараллельные прямые – различные. Обычные точки будем называть собственными. Прямую, дополненную несобственной точкой, назовём расширенной. Каждая плоскость имеет бесконечное множество параллельных прямых, следовательно и несобственных точек. Пусть все несобственные точки плоскости образуют несобственные прямые, а все несобственные точки пространства - несобственную плоскость. Плоскость, дополненную расширенной прямой, будем называть расширенной плоскостью. Вот и построена нами новая геометрия, которая занимает не менее важное место, чем евклидова.

Другим важнейшим результатом работы Дезарга является его исследование так называемого инволюционного соответствия точек прямолинейного ряда. Здесь и самый термин «инволюция» принадлежит Дезаргу и взят им из ботанического словаря, в котором слово «инволюция» означает скручивание молодых листьев. Прямую, на которой расположен ряд точек, он называет «древом», точку отсчета отрезков – «стволом», самые отрезки – «ветвями» и т.д. Это соответствие находит свое применение в принципе двойственности проективной геометрии: «если справедливо утверждение Δ, в котором говорится о точках и прямых на плоскости и об их взаимном расположении, то справедливо и двойственное предложение Δ* которое получается из Δ заменой слова «точка» словом «прямая», а слова «прямая» словом «точка».

Н

Ж. Жергони

апример, если рассматривать предложение Δ= «Каждой прямой принадлежит бесконечное множество точек», то двойственное примет вид Δ*= «Каждой точке принадлежит бесконечное множество прямых» - или, перефразируя «Через каждую точку проходит бесконечное множество прямых». Причем, если справедливо исходное утверждение, то справедливо и ему двойственное. Аналогичный принцип двойственности существует и в пространстве, причем слово «точка» заменяется словом «плоскость», а «плоскость» - «точка», а прямая остается прямой. Впервые принцип двойственности был открыт в 1825 году французским математиком Ж.Жергонн. Он впервые предложил записывать аналогичные утверждения для плоскости и пространства в два столбца. Например, для утверждения «В любой треугольник можно вписать окружность, и притом только одну» двойственным будет «В любой тетраэдр можно вписать сферу, и притом только одну!» Пользуясь этим принципом, совсем не обязательно каждый раз доказывать пространственный аналог какого-то плоскостного утверждения, так как если выполняется исходное утверждение, то непременно будет выполняться и двойственное.

Все теоремы проективной геометрии касаются только проективных свойств, в них даже и не говорится ни об углах, ни о длинах. Одна из известных теорем проективной геометрии – это теорема Дезарга. Теорема Дезарга дает ответ на детскую задачку: как посадить десять деревьев десятью рядами так, чтобы в каждом ряду было по три дерева.

Сформулируем теорему. Пусть на плоскости заданы точки А, В, С и точка О, через которую проходят прямые ОА, ОВ, ОС. На каждой из этих прямых выберем по одной произвольной точке – А₁, В₁, С₁, тогда точки пересечения прямых АВ с А₁В₁, АС с А₁С₁ и ВС с В₁С₁ лежат на одной прямой.

Особенность этой теоремы еще и в том, что в теореме соблюдается полное равноправие: любые четыре из этих точек можно обозначить через А, В, С, О, и содержание теоремы не изменится.

Другая особенность в том, что в теореме Дезарга можно «поменять местами» точки и прямые: записывая формулировку теоремы будем вместо слов «точка лежит на прямой» писать «прямая проходит через точку», и наоборот, то есть слова «точка» и «прямая» можно менять местами. В результате такой «лингвистической» процедуры прямая теорема Дезарга превратится в так называемую обратную.

Оказывается, в проективной геометрии такое же «преобразование» можно применить к тексту любой теоремы. Ведь на проективной плоскости, в отличие от евклидовой, нет параллельных прямых. Любые две прямые имеют общую точку. И, конечно же, через любые две точки проходит единственная прямая.

Таким образом, если доказана какая-либо теорема проективной геометрии, то можно считать доказанной и двойственную ей теорему, которая получается из нее, если поменять местами точки и прямые.

Как уже говорилось, в проективной геометрии между двумя точками расстояние изменяется. Но положение изменится, если на прямой задано четыре точки или четыре объекта. Пусть это точки А, В, С, D. Возьмем в качестве отсчета некоторую точку О и измерим расстояние от этой точки до каждой из заданных. Предположим их равными a, b, c, d. Вычислим величину . Это число обладает тем свойством, что оно одно и то же для изображения и его оригинала. То есть, если мы измерим расстояние между четырьмя объектами, например, между четырьмя городами, а затем сфотографируем эти города с высоты птичьего полета, то и в первом, и во втором случае это отношение будет одним и тем же. Эта величина х носит свое название, она называется сложным отношением четырех точек. Это число может быть, как положительным, так и отрицательным. Значение сложного отношения, равного (-1) представляет наибольший интерес. В этом случае оно называется гармоническим, а числа говорят, образуют, гармоническую четверку. То есть они расположены гармонично по отношению друг к другу, и в частности, длины отрезков играют некоторую роль в теории гармоники (в теории музыкальных инструментов).

Из простейших фигур евклидовой геометрии можно вспомнить треугольники, четырехугольники, окружности. Есть ли похожие понятия в проективной геометрии?

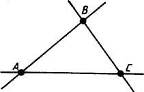
Начнем с аналога треугольника. Он называется трехвершинником. Трехвершинником называется фигура, состоящая из трех точек, не лежащих на одной прямой, и трех прямых, соединяющих попарно эти точки. Указанные точки называются вершинами, а прямые — сторонами трехвершинника. Трехвершинник с вершинами А, В, С обозначается так: АВС (рис. 30).

Поскольку, как было сказано выше, точки прямые в проективной геометрии равноправны, можно ввести новую фигуру, дав ей следующее определение: фигура, состоящая из трех прямых, не лежащих на одной точке (то есть не проходящих через одну точку), и трех точек, соединяющих попарно эти прямые, называется трехсторонником.

Другая фигура проективной геометрии – это полный четырехвершинник, аналог четырехугольника.

Полным четырехвершинником называется фигура, состоящая из четырех точек проективной плоскости, никакие три из которых не лежат на одной прямой, и шести прямых, соединяющих попарно эти точки. Указанные точки называются вершинами, а прямые — сторонами полного четырехвершинника. Стороны, не имеющие общей вершины, н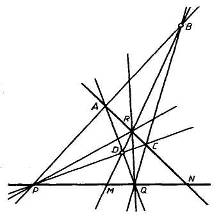 азываются противоположными. В четырехвершиннике ABCD противоположными являются стороны АВ и CD, ВС и DA, АС и BD. Точки пересечения противоположных сторон называются диагональными точками, а прямые, попарно соединяющие диагональ­ные точки,— диагоналями полного четырехвершинника (рис.31 ).

Особенностью диагональных точек является то, что они при любом расположении точек четырехвершинника не лежат на одной прямой.

Другая особенность заключается в определенной, никогда не меняющейся их связи с вершинами.

1) На каждой диа­гонали полного четырехвершинника диагональные точки гармо­нически разделяют две точки, в которых эта диагональ пересекает стороны, проходящие через третью диагональную точку.

2) Две вершины, лежащие на стороне полного четырехвершинника, гармонически разделяют пару точек, состоящую из диагональной точки и точки, в которой эта сторона пересекает диагональ, проходящую через две другие диагональные точки.

Следуя принципу двойственности, справедливо и третье утверждение.

3)Две противоположные стороны полного четы­рехвершинника гармонически разделяют две диагонали, проходящие через точку пересечения этих сторон.

Рассуждая по аналогии, можно заключить, что существуют и пятивершинники, и шестивершинники – как и в евклидовой геометрии выделяют многоугольники.

По аналогии с окружностью в проективной геометрии выделяется овальная кривая второго порядка. Она задается уравнением вида .

Ряд особенностей окружности сохраняется и для нее. Так, например, любая прямая, проходящая через внутреннюю точку овальной кривой, пересекает ее в двух точках, в любой точке овальной кривой существует касательная.

Проективная геометрия, как раздел геометрии, занимает свое особенное место в списке известных на настоящее время геометрий.

С вое практическое значение проективная геометрия реализовывает в различных проектах и архитектурных планах, в строительстве водонапорных башен и телевизионных матч.

Готовый вариант монастыря