10.2. Знакочередующиеся ряды Краткие теоретические сведения

Определение. Ряд называют знакочередующимся, если среди его членов есть бесконечно много как положительных, так и отрицательных членов. Частным случаем знакопеременного ряда является знакочередующийся ряд 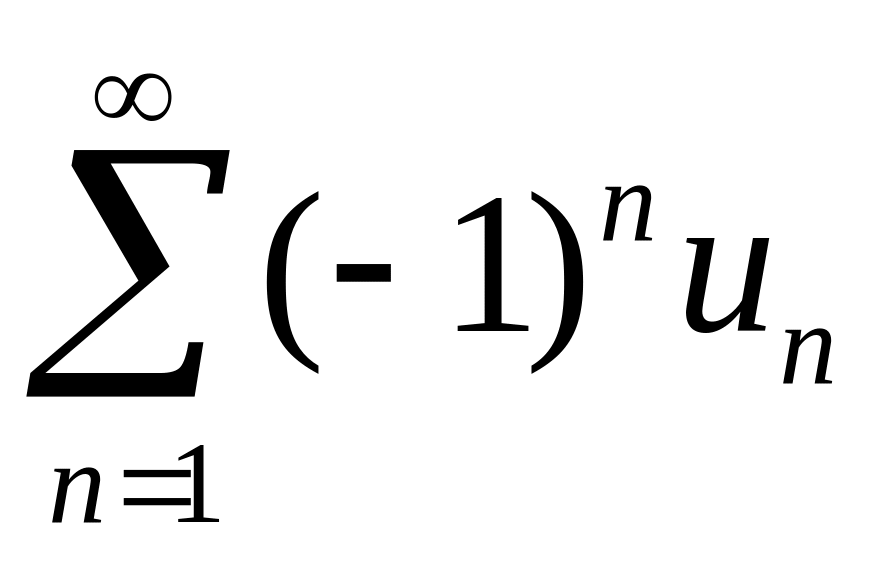, где N: (1).

Составим ряд (2) из абсолютных величин членов ряда (1):

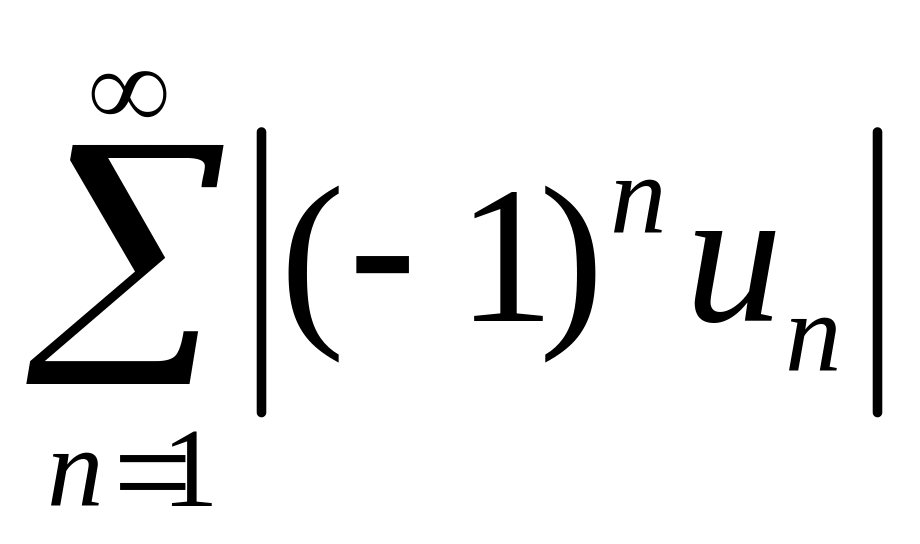(2).

Если ряд (1) сходится вместе с рядом (2), то ряд (1)называется абсолютно сходящимся. Если ряд (1) сходится, а ряд (2) расходится, то ряд (1) называется условно сходящимся.

Теорема 1. Сходящийся знакочередующийся ряд (в том числе и знакоположительный) остается сходящимся и не меняет своей суммы при любой группировке его членов, произведенной без изменения порядка их следования.

Теорема 2. Абсолютно сходящийся ряд (в том числе и знакоположительный) остается и не меняет своей суммы при любой перестановке его членов.

Теорема 3. Изменяя порядок следования в условно сходящемся ряде, можно сделать сумму ряда равной любому наперед заданному числу или даже сделать ряд расходящимся.

Теорема 4. Если ряд (2) сходится, то ряд (1) сходится абсолютно.

Признак Лейбница. Если:

1) –знакочередующийся ряд;

2) N: ;

3) ,

то сходится.

Исследование сходимости знакочередующихся рядов следует начинать с исследования их абсолютной сходимости, так как это часто быстрее приводит к цели, чем применение признака Лейбница с последующим исследованием абсолютной сходимости.

Признак Абеля. Если для ряда 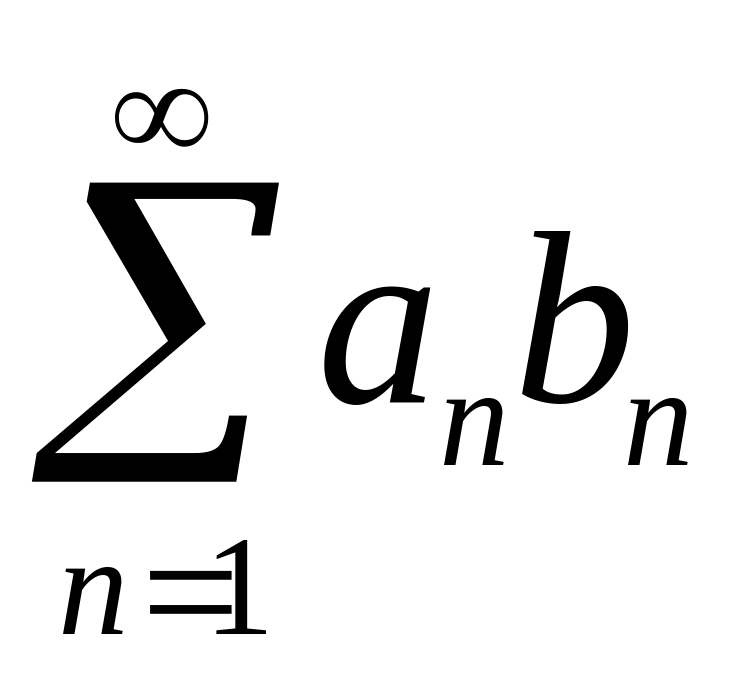выполняются условия:

1) ряд сходится;

б) последовательность монотонная и ограниченная,

то ряд сходится.

Признак Дирихле. Если для ряда выполняются условия:

а) последовательность частичных сумм { } ограничена;

б) последовательность { } монотонно стремится к 0,

то ряд сходится.

Для приближенного вычисления суммы сходящегося ряда полагают 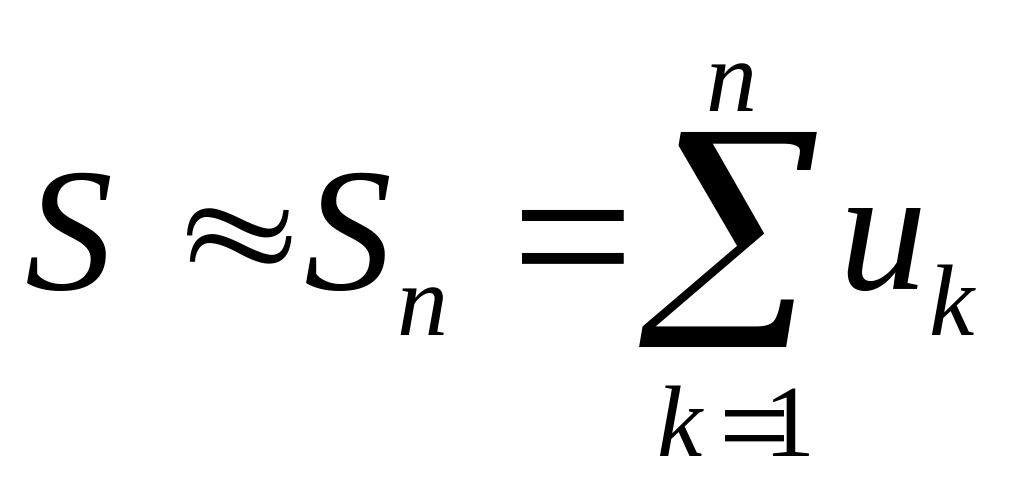, пренебрегая остатком .

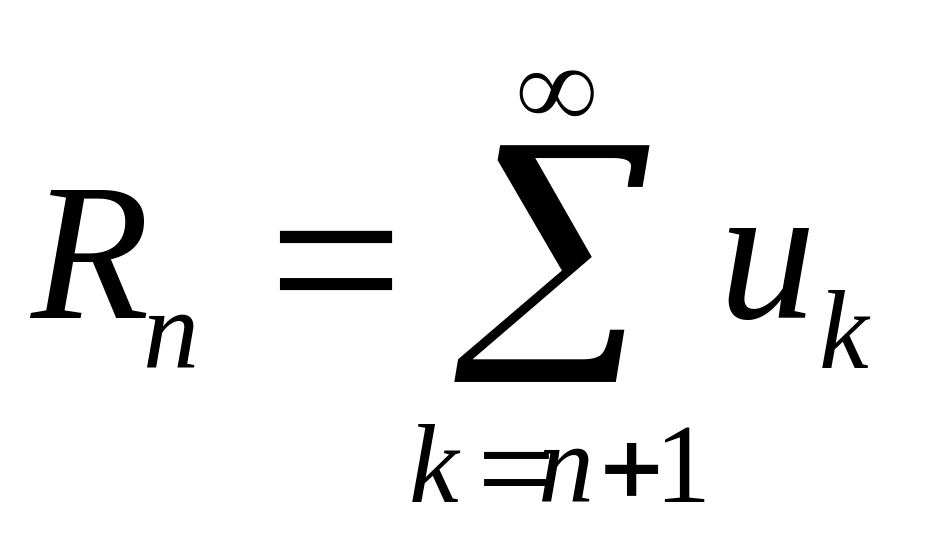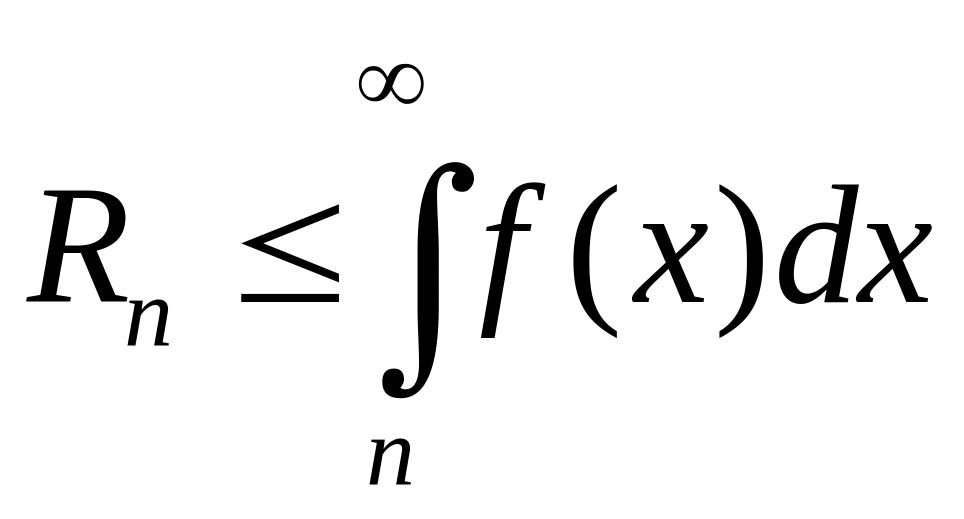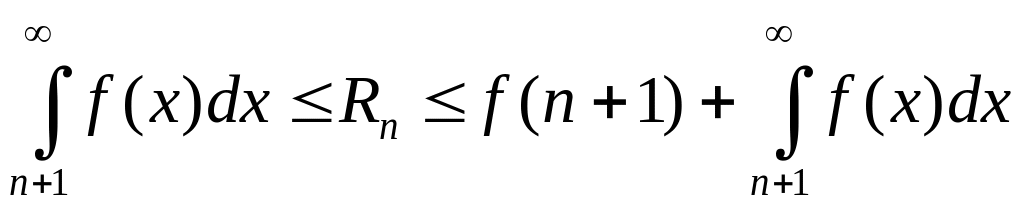Для сходящихся знакоположительных рядов, члены которых монотонно убывают, начиная с , справедливы следующие оценки остатка или , где – общий член ряда.

Примеры решения типовых задач

Пример 1. Исследовать на сходимость ряд

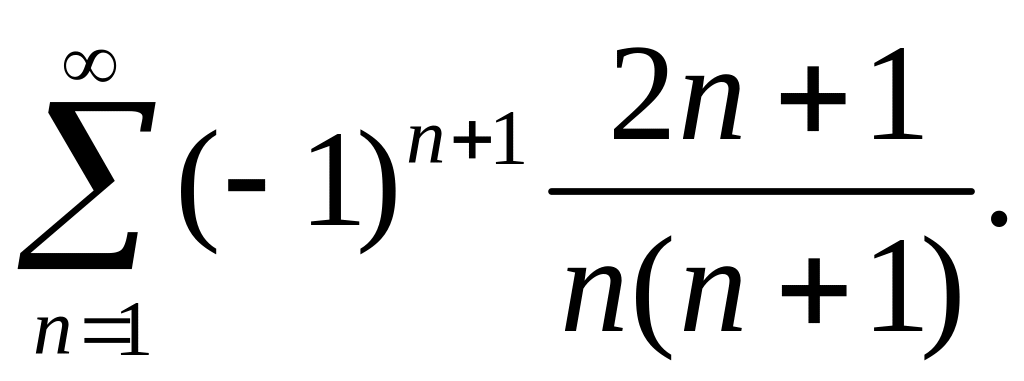
Решение. Этот ряд знакочередующийся. Применим признак Лейбница. Проверим выполнение первого условия.

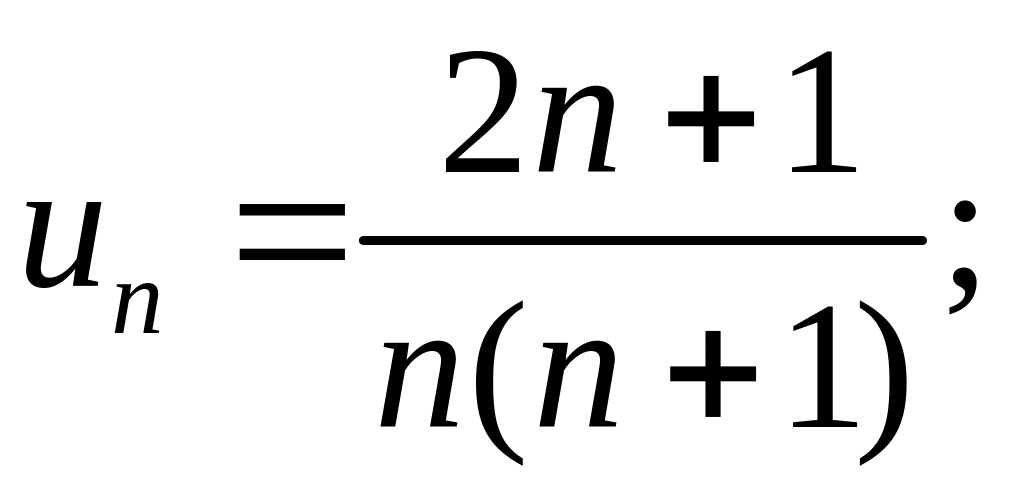
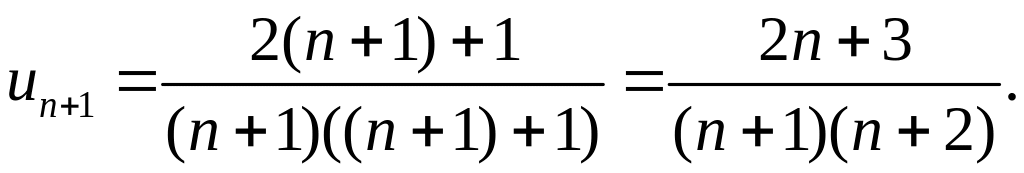
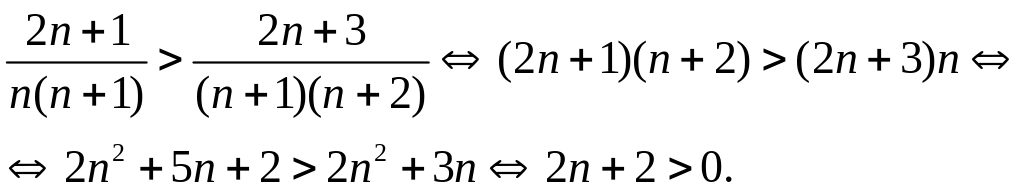
Выполнение второго условия очевидно

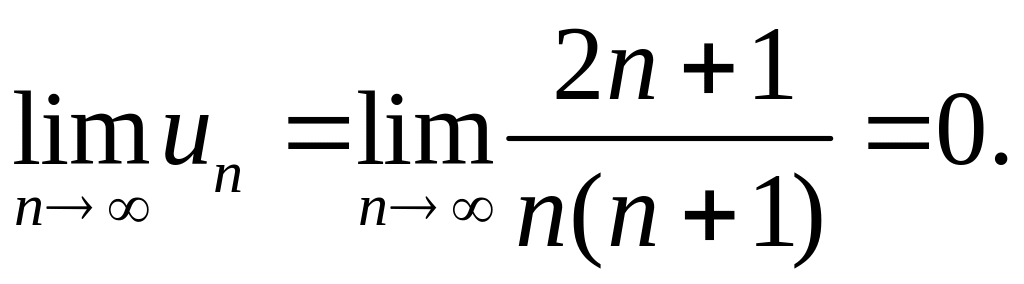
Значит, выполнены оба условия признака Лейбница. Следовательно, данный ряд сходится. Исследуем на сходимость ряд, составленный из абсолютных величин членов первоначального ряда 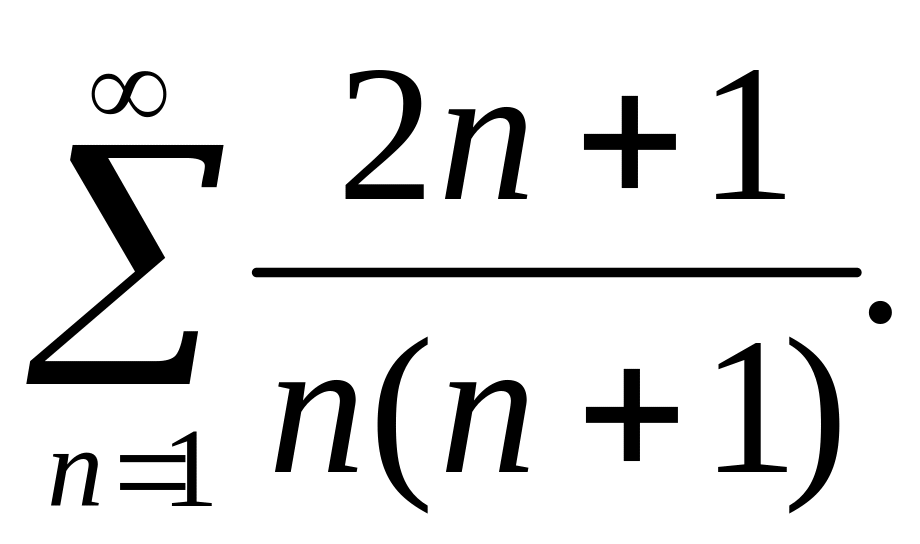Покажем, что ряд и гармонический ряд ведут себя одинаково.

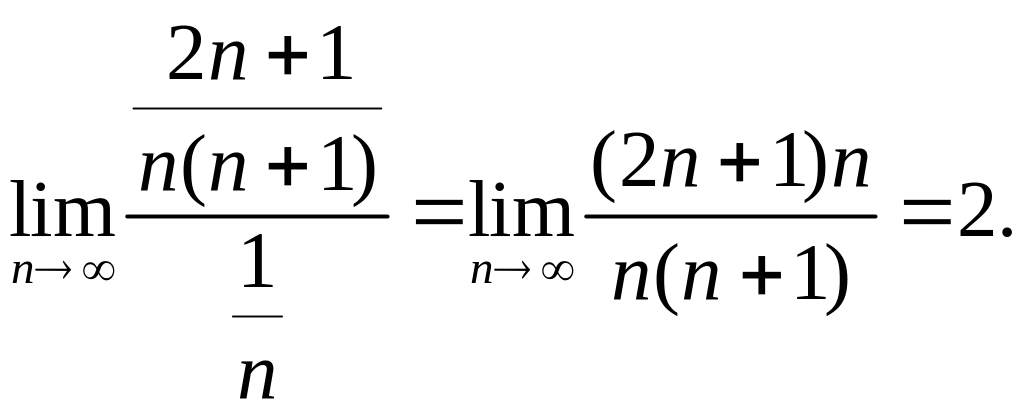Значит ряд, составленный из абсолютных величин, расходится. Таким образом, что исходный ряд сходится условно.

Пример 2. Исследовать на сходимость ряд. .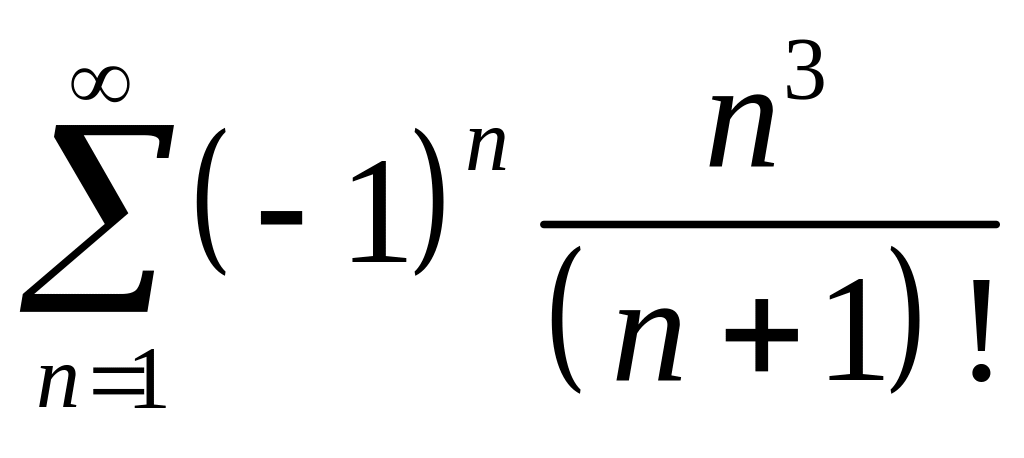

Решение. В данном примере сначала исследуем знакочередующийся ряд на абсолютную сходимость, т.е. исследуем сходимость ряда, составленного из абсолютных величин членов данного ряда .

По признаку Даламбера

.

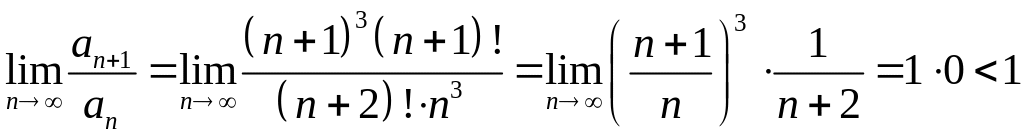Ряд из абсолютных величин сходится, следовательно, данный знакочередующийся ряд сходится абсолютно.

Пример 3. Найти сумму ряда .

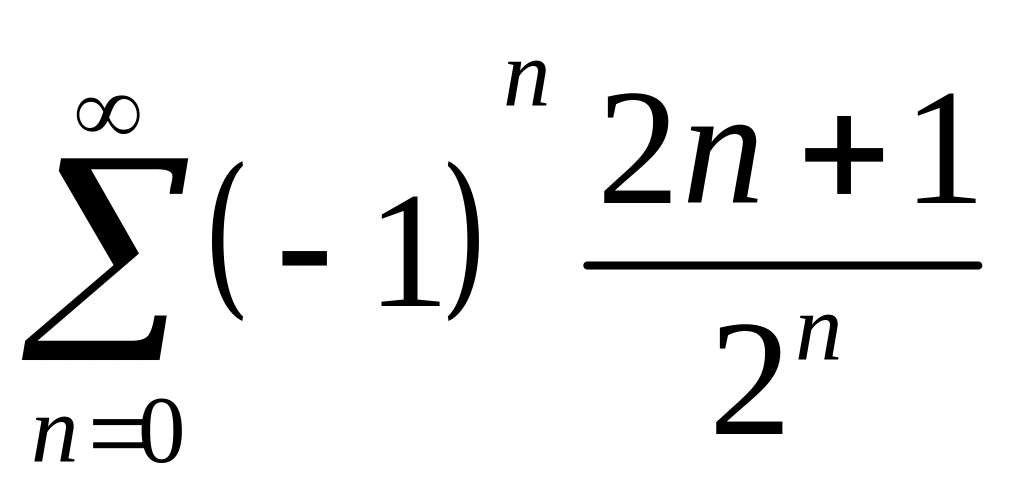Решение. Составим последовательность частичных сумм ,

,

,

т.е. , тогда

.

Следовательно, .

Пример 4. Сколько членов ряда 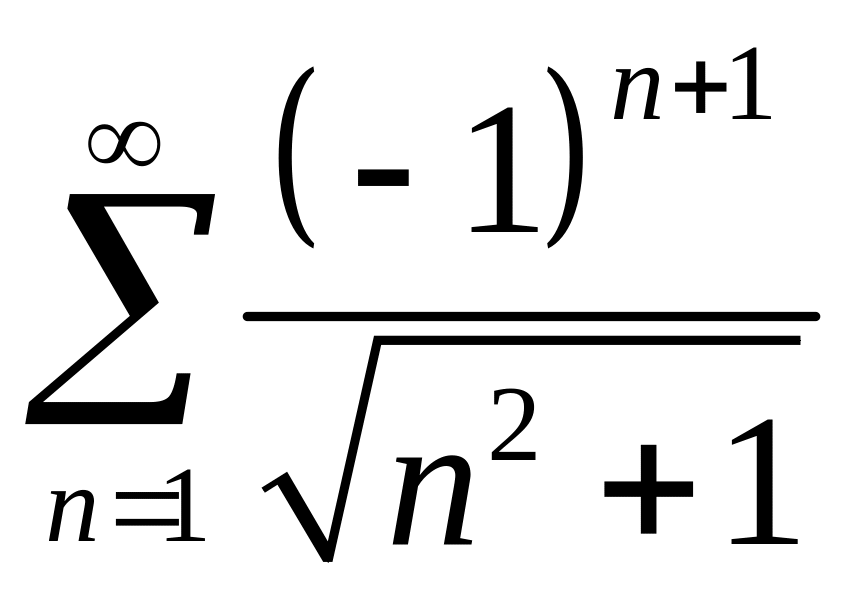следует взять, чтобы получить сумму ряда с точностью до ?

Решение. Данный знакочередующийся ряд сходится по признаку Лейбница. Если возьмем , то ошибка не превосходит 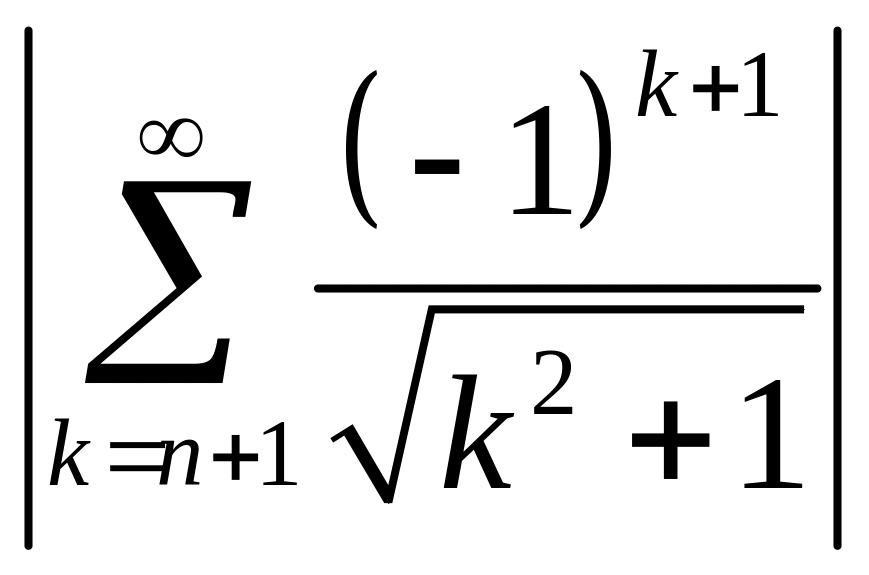. Но для знакочередующихся рядов остаток ряда по абсолютной величине не превосходит величины своего первого члена, т.е. 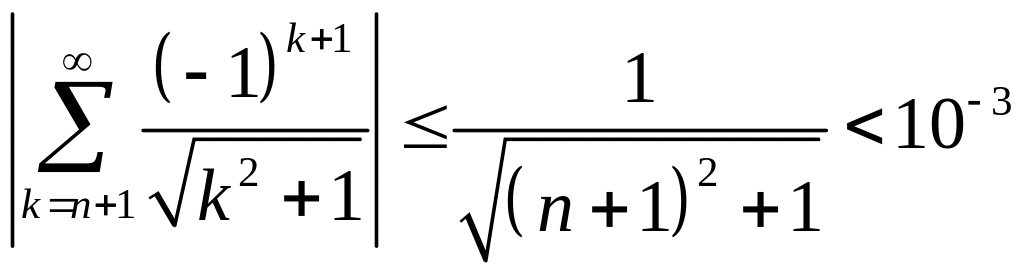, что верно при . Отсюда ясно, что достаточно взять 999 членов ряда. Тогда получим требуемую точность.

Пример 5. Исследовать на сходимость ряд .

Решение. 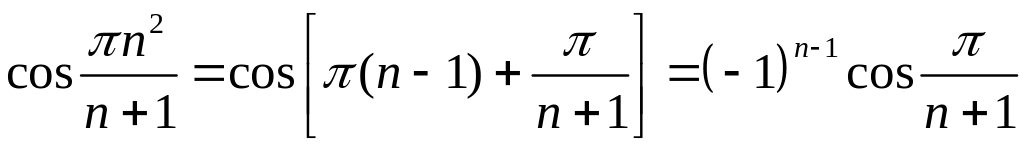, поэтому данный ряд имеет ви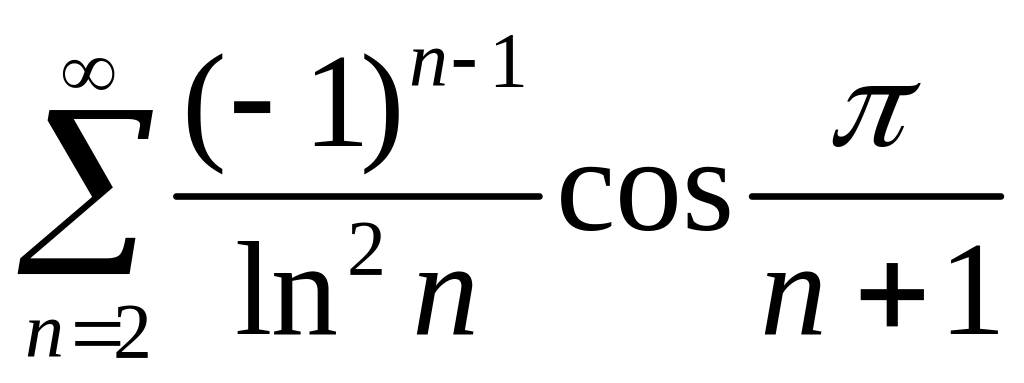д . Но ряд сходится по признаку Лейбница, а 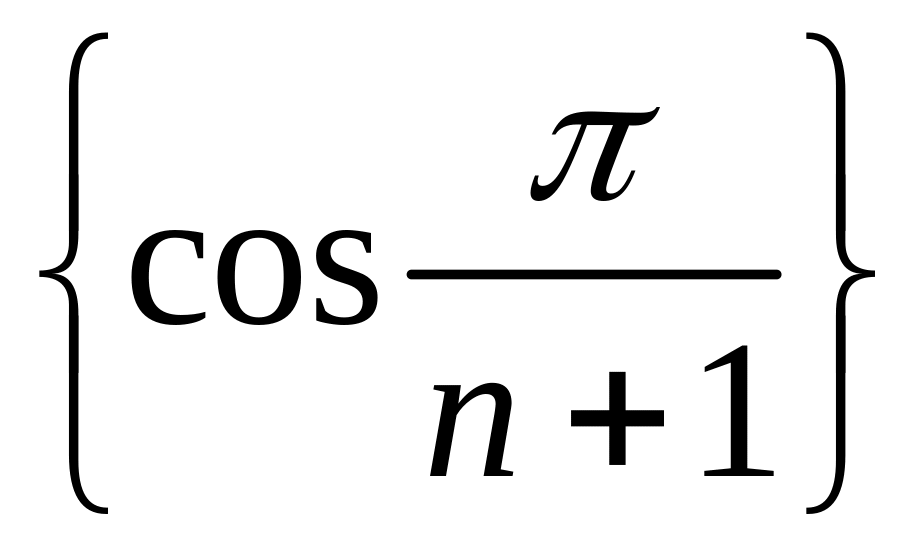монотонная и ограниченная последовательность. Значит, по признаку Абеля исходный ряд сходится.

Рассмотрим ряд из абсолютных величин 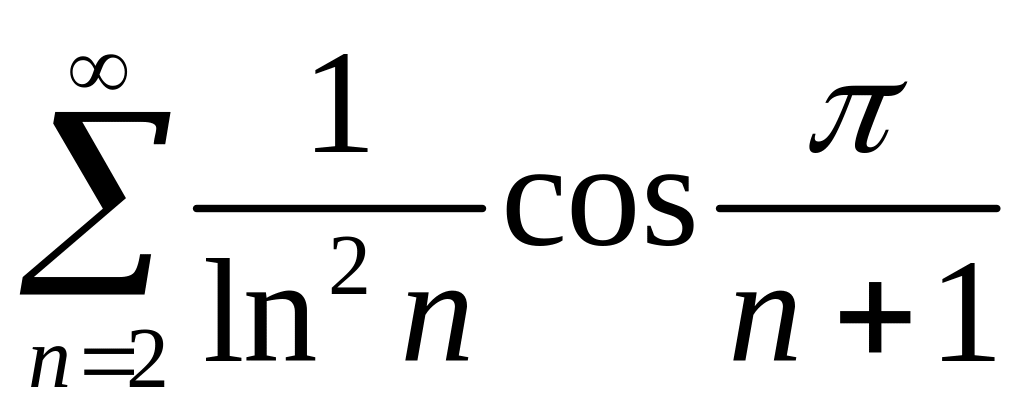. Так как ~ при и начиная с некоторого n, а расходится, то расходится. Значит, данный ряд расходится условно.

Пример 6. Вычислить сумму ряда 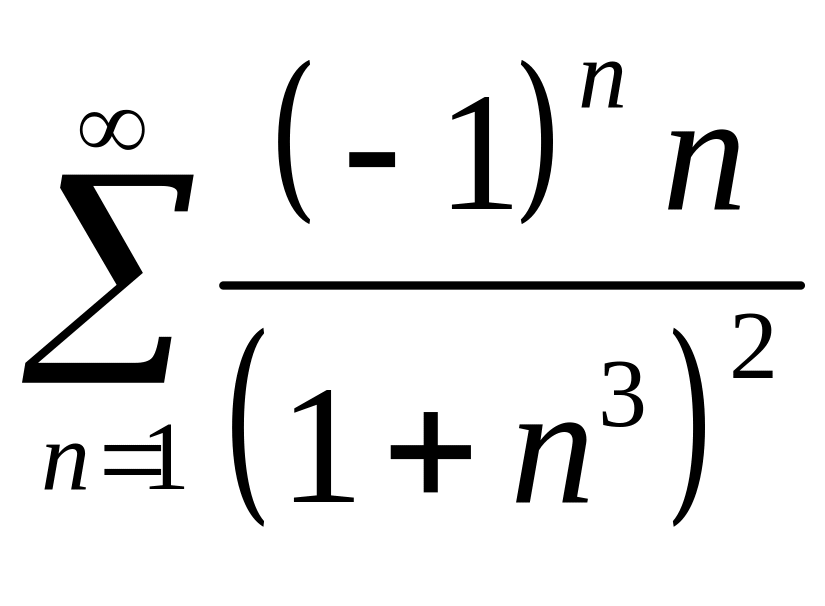с точностью до 0,001.

Решение. Для знакочередующихся рядов погрешность не превышает первого отброшенного члена.

.

,

,

,

.

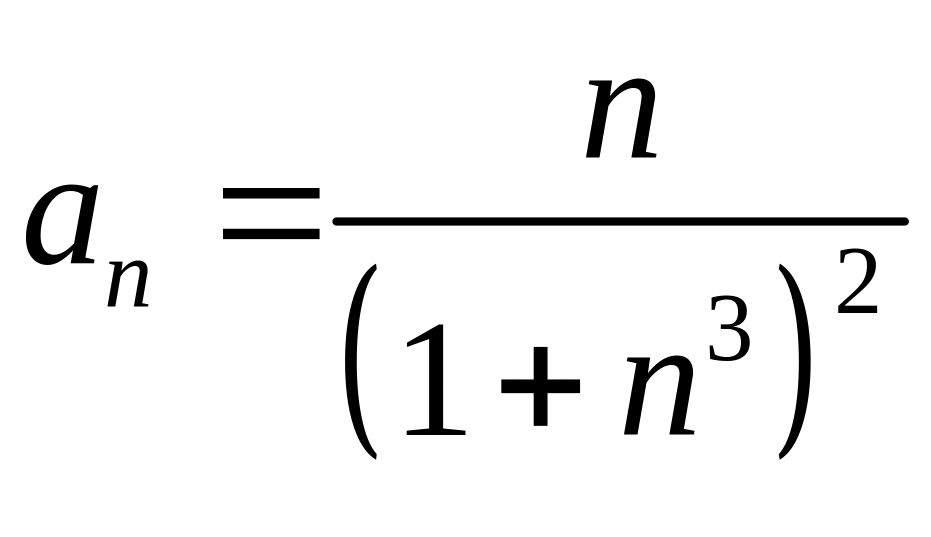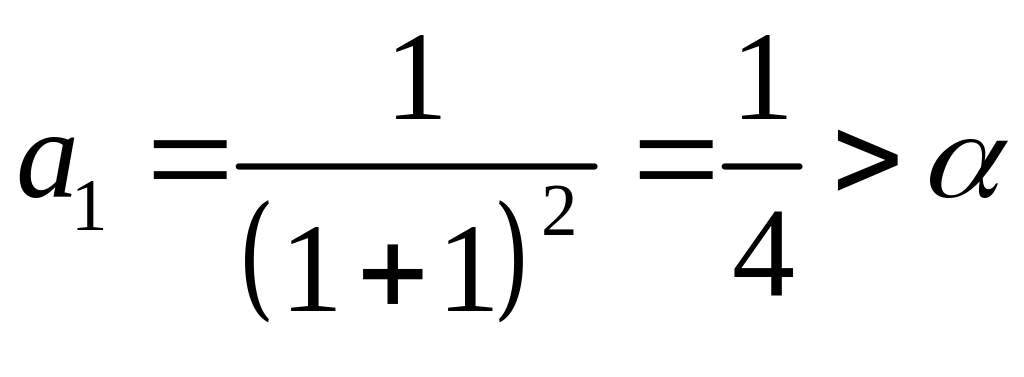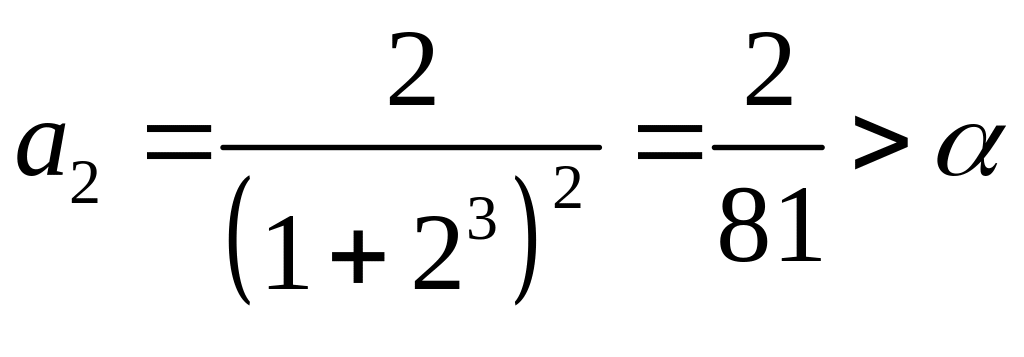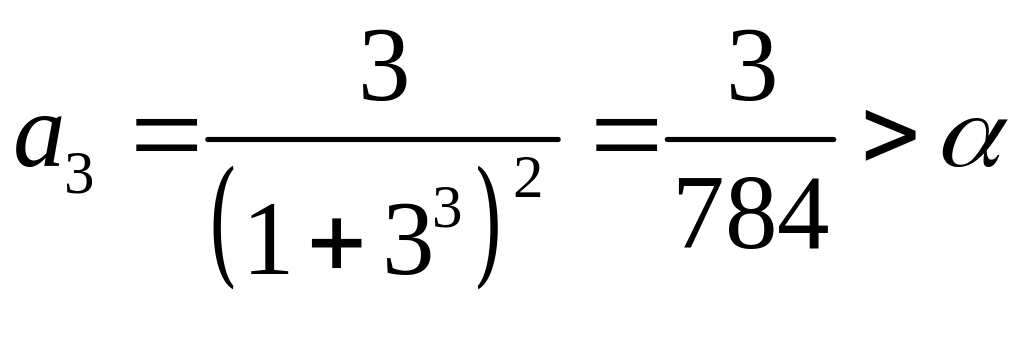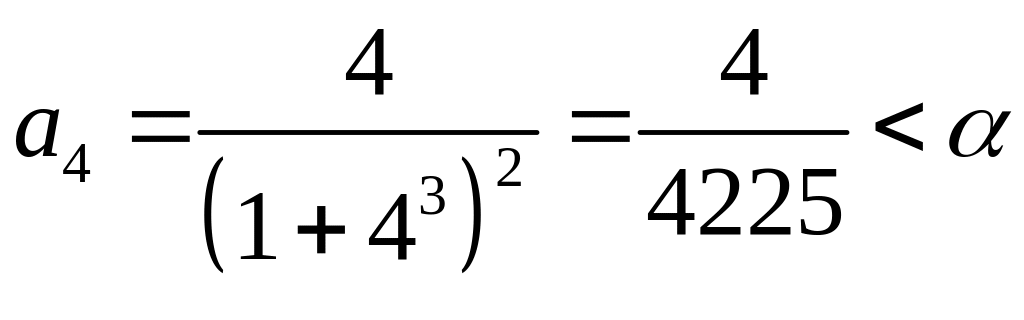Поэтому искомая сумма с точностью до равна

.

Пример 7. Доказать справедливость равенства .

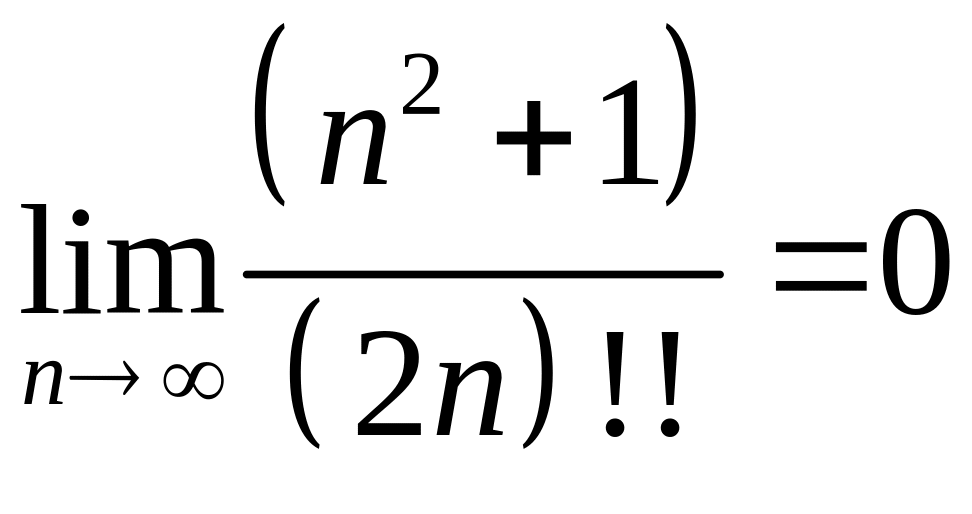Решение. Рассмотрим ряд 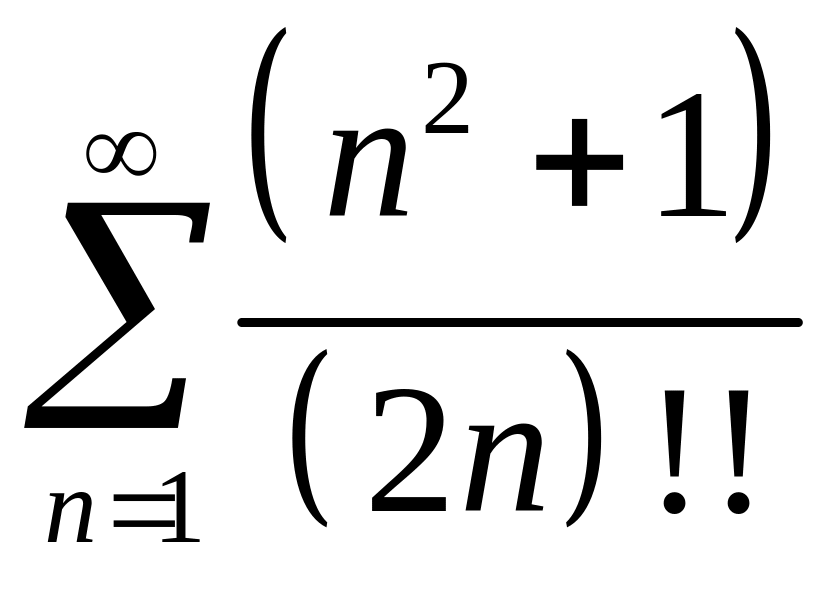. Исследуем его сходимость по признаку Даламбера:

.

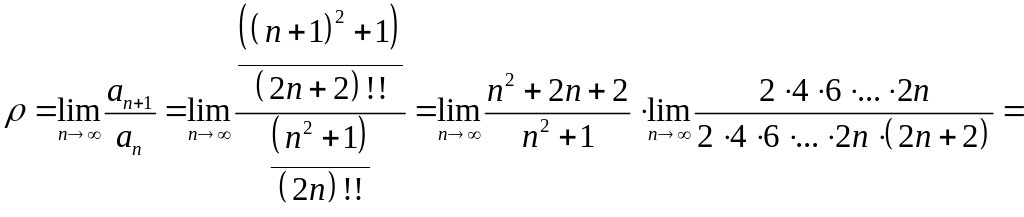
Ряд сходится. Следовательно, по необходимому признаку предел общего члена равен нулю.