
- •I Понятие функции двух и более переменных, область определения функции
- •Примеры для самостоятельного решения
- •II Частные производные функции нескольких переменных
- •Примеры для самостоятельного решения
- •III Полный дифференциал функции нескольких переменных. Дифференциалы высших порядков
- •Примеры для самостоятельного решения
- •IV Производная по направлению и градиент
- •Примеры для самостоятельного решения
- •V Экстремум функций нескольких переменных
- •Примеры для самостоятельного решения
- •VI Условный экстремум
- •Задачи для самостоятельного решения
- •VII Наибольшее и наименьшее значения функции
- •Примеры для самостоятельного решения
- •Литература
Примеры для самостоятельного решения
I. Найти производную функции по направлению вектора в точке М, если:
1.
![]() ;
;
2.
![]() ;
;
3.
![]() ;
;
4.
![]() ;
;
5.
![]() .
.
II. Найти производную функции в точке по направлению вектора , если
1.
![]() ;
;
2.
![]() ;
;
3.
![]() ;
;
4.
![]() ;
;
5.
![]() ;
;
6.
![]() ;
;
7.
![]() ;
;
8.
![]() .
.
Найти производную функции в точке М по данному направлению, если:
1.
![]() ,
по направлению вектора, образующего с
осью ОХ угол
,
по направлению вектора, образующего с
осью ОХ угол
![]() .
.
2.
![]() ;
;
3.
![]() ;
;
4.
![]() ;
;
5.
![]() .
.
Найти градиент функции в точке М, если:
1.
![]() ;
3.
;
3.
![]() ;
;
2.
![]() ;
4.
;
4.
![]() ;
;
5.
![]() .
.
Найти наибольшее значение в точке М, если:
1.
![]() ;
3.
;
3.
![]() ;
;
2.
![]() ;
4.
;
4.
![]() .
.
Найти вектор , по направлению которого в точке М достигает наибольшего значения, если:
1.
![]() ;
3.
;
3.
![]() ;
;
2.
![]() ;
4.
;
4.
![]() .
.
V Экстремум функций нескольких переменных
Пусть функция
![]() определена в окрестности точки
определена в окрестности точки
![]() .
.
Определение 1. Если
существует окрестность
![]() ,
в которой
,
в которой
![]()
![]() ,
то точка М0
называется точкой локального максимума
(минимума) функции
.
,
то точка М0
называется точкой локального максимума
(минимума) функции
.
Точки локального минимума и максимума называются точками локального экстремума.
Теорема 1. (Необходимые условия локального экстремума).
Если дифференцируемая
функция
![]() имеет экстремум в точке М0,
то частные производные первого порядка
по всем переменным от
равны нулю, то есть
имеет экстремум в точке М0,
то частные производные первого порядка
по всем переменным от
равны нулю, то есть
![]() .
.
Назовем точки, в которых все частные производные функции равны нулю, стационарными.
Итак, если М0 – точка локального экстремума дифференцируемой функции, то она обязательно стационарная. Обратное утверждение в общем случае неверно. Это подтверждает следующий пример.
Пример 1. Пусть
дана дифференцируемая функция
![]() .
.
Найдем ее стационарные
точки:
![]() при
при
![]() .
.
Значение функции
![]() в стационарной точке (0;0) равно нулю,
но, очевидно, в сколь угодно малой
окрестности этой точки, функция
принимает как положительные, так и
отрицательные значения. (Поясните!).
Следовательно, в стационарной точке
(0;0) наша функция экстремума не имеет.
в стационарной точке (0;0) равно нулю,
но, очевидно, в сколь угодно малой
окрестности этой точки, функция
принимает как положительные, так и
отрицательные значения. (Поясните!).
Следовательно, в стационарной точке
(0;0) наша функция экстремума не имеет.
Если не ограничиваться рассмотрением только дифференцируемых функций, то необходимое условие локального экстремума нужно дополнить. Если функция имеет экстремум в точке М0, то а) или все частные производные первого порядка равны нулю в точке М0; б) или хотя бы одна из частных производных первого порядка не существует в точке М0.
Такие точки М0 называются критическими точками.
Теорема 2. (Достаточные условия локального экстремума функций нескольких переменных)
Пусть
![]() --
функция нескольких переменных, имеющая
в некоторой окрестности своей стационарной
точки М0
непрерывные частные производные второго
порядка. Тогда
--
функция нескольких переменных, имеющая
в некоторой окрестности своей стационарной
точки М0
непрерывные частные производные второго
порядка. Тогда
1) если
![]() при всех
при всех
![]() одновременно не равных нулю, то М0
– точка локального минимума
;
одновременно не равных нулю, то М0
– точка локального минимума
;
2) если
![]() при всех
одновременно не равных нулю, то М0
– точка локального максимума
;
при всех
одновременно не равных нулю, то М0
– точка локального максимума
;
если
 меняет знак, то есть при одном наборе
меняет знак, то есть при одном наборе
 положителен, а при другом наборе
положителен, а при другом наборе
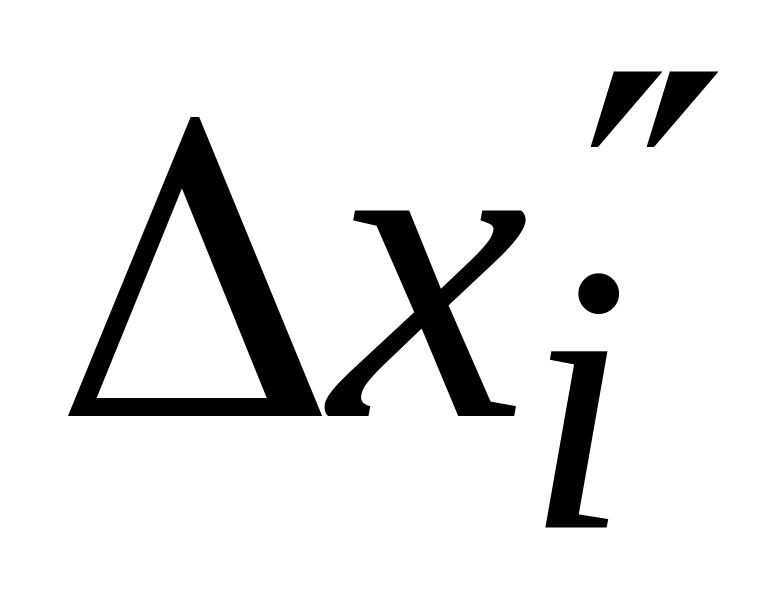 отрицателен, то в точке М0
экстремума
нет;
отрицателен, то в точке М0
экстремума
нет;если
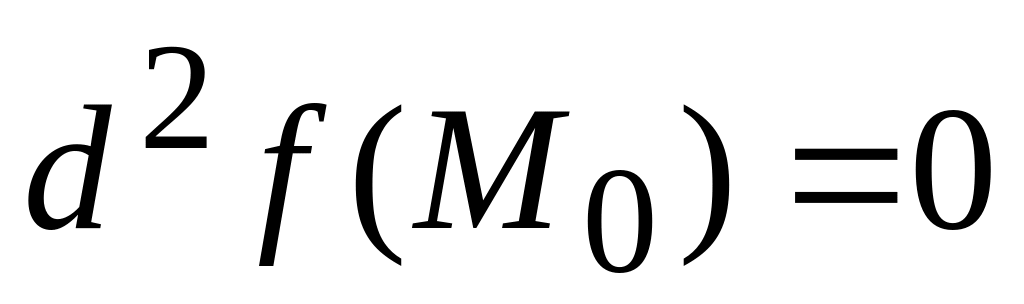 ,
то есть
,
то есть
 ,
то ничего определенного сказать нельзя,
то есть экстремум в точке М0
может быть, а может и не быть.
,
то ничего определенного сказать нельзя,
то есть экстремум в точке М0
может быть, а может и не быть.
Дифференциал второго
порядка любой функции – квадратичная
форма:
![]() ,
где
,
где
![]() --
действительные числа. В развернутом
виде квадратичная форма записывается
следующим образом:
--
действительные числа. В развернутом
виде квадратичная форма записывается
следующим образом:
![]()
![]() .
.
Определение 2. Матрицу
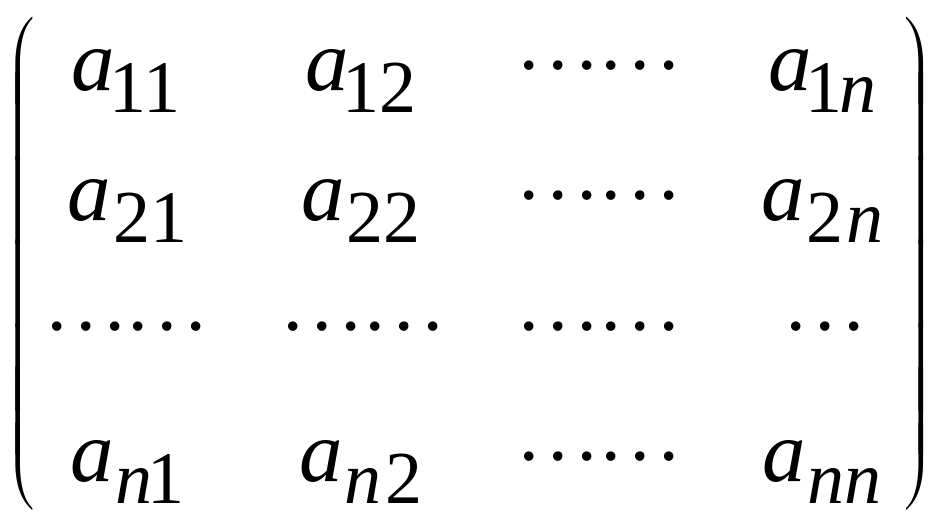 называют матрицей квадратичной формы.
называют матрицей квадратичной формы.
Определение 3. Квадратичная форма называется положительно определенной, если при всех одновременно не равных нулю; отрицательно определенной, если при всех одновременно не равных нулю; знакопеременной, если найдутся два набора такие, что при одном из них , а при другом ; неопределенной, если хотя бы для одного нетривиального набора .
Теорема 3. (Критерий Сильвестра). Для того чтобы квадратичная форма была 1) положительно определенной, необходимо и достаточно, чтобы все главные миноры ее матрицы были положительны, то есть
![]()
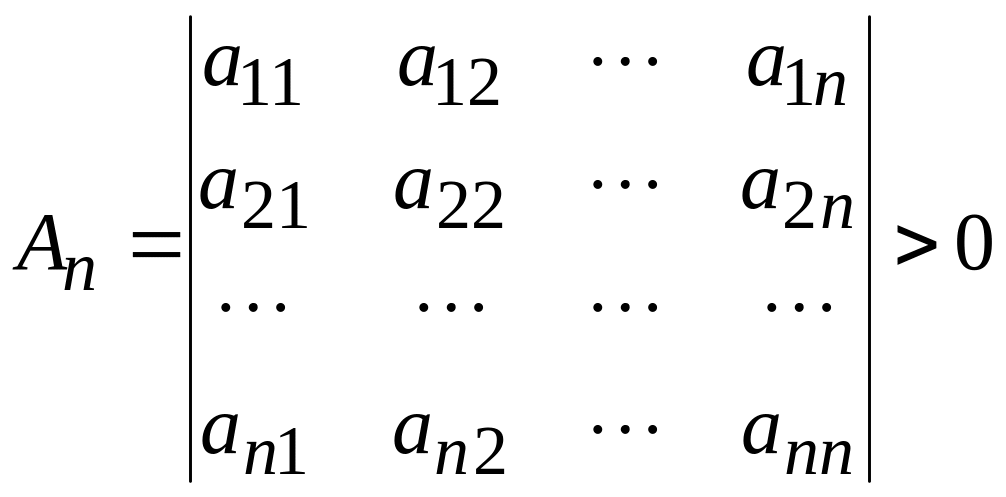 ;
;
2) отрицательно
определенной, необходимо и достаточно,
чтобы знаки главных миноров чередовались,
причем
![]() .
.
3) Если среди главных миноров нет ни одного нуля, но не выполняются ни условие 1), ни 2), то квадратичная форма знакопеременная;
4)если среди главных миноров хотя бы один нуль, то она неопределенная.
Для функций двух переменных
![]()
![]() .
.
Обозначим через
![]() .
.
Используя определение определенности квадратичной формы и теорему 3, из теоремы 2 следует результат:
Теорема 4. (Достаточные условия существования локального экстремума функции двух переменных).
Пусть функция
имеет в некоторой окрестности своей
стационарной точки
![]() непрерывные частные производные второго
порядка. Тогда
непрерывные частные производные второго
порядка. Тогда
1) если
![]() ,
то при
,
то при
![]() М0
– точка локального максимума, а
М0
– точка локального максимума, а
при
![]() М0
– точка локального минимума;
М0
– точка локального минимума;
2) если
![]() ,
то в точке М0
экстремума нет;
,
то в точке М0
экстремума нет;
3) если
![]() ,
то ничего сказать нельзя.
,
то ничего сказать нельзя.
Заметим, что из условия
вытекает, что
![]() .
.
Схема нахождения локального экстремума функций нескольких переменных.
Найти все стационарные точки функции ;
Определить точки, где не существуют частные производные;
Вычислить
 в каждой стационарной точке и выяснить
знак
;
в каждой стационарной точке и выяснить
знак
;Сделать вывод об экстремуме, если сразу ясен знак ;
Если знак сразу не ясен, то необходимо выписать матрицу квадратичной формы, вычислить главные миноры и сделать вывод об определенности квадратичной формы и об экстремуме. (В случае функции двух переменных воспользоваться результатом теоремы 4);
В точках, где не существуют частные производные функции , нужно записать полное приращение функции, определить его знак в окрестностях этих точек и сделать вывод об экстремуме (если полное приращение положительно в окрестности точки М0, то М0 – точка локального минимума, если – отрицательно, то М0 – точка локального максимума).
Замечание. При выяснении знака можно переменные менять местами, если среди главных миноров есть нулевые, эта операция не приводит к результату, если определитель всей матрицы равен нулю.
Пример 2. Исследовать на локальный экстремум функцию:
![]() .
.
Функция определена
при всех
и
.
Найдем частные производные первого
порядка:
![]() ;
;
![]() .
.
Эти производные
существуют для всех
и
.
Для нахождения стационарных точек
имеем:
![]() или
или
![]() .
.
Так как
![]() не является решением системы, то
не является решением системы, то
![]() .
.
Умножим обе части
уравнения на
![]() ,
получим
,
получим
![]() .
.
Далее,
![]() ;
;
![]() или
или
![]() .
.
То есть
![]() -- стационарные точки.
-- стационарные точки.
Вычислим частные производные второго порядка:
![]() .
.
Тогда в точке (2;3)
имеем:
![]()
![]() .
.
Значит согласно достаточному условию теоремы 4, в этой точке нет экстремума.
В точке (-2;-3):
![]() --
также нет экстремума.
--
также нет экстремума.
В точке (3;2):
![]() -- экстремум есть, и
так как
-- экстремум есть, и
так как
![]() ,
то это точка локального минимума.
,
то это точка локального минимума.
![]() .
.
В точке (-3;-2):
![]() -- экстремум есть, и
так как
-- экстремум есть, и
так как
![]() ,
то это точка локального максимума.
,
то это точка локального максимума.
![]() .
.
Пример 3. Исследовать на локальный экстремум функцию:
![]() .
.
Найдем частные производные и составим систему уравнений.
![]() или
или
![]() Решая систему,
получим четыре стационарные точки
Решая систему,
получим четыре стационарные точки
![]()
![]() .
Найдем частные производные второго
порядка
.
Найдем частные производные второго
порядка
![]() .
.
Запишем дифференциал второго порядка функции:
![]() .
.
1) Вычислим
![]() в точке
в точке
![]() :
:
![]() .
.
Матрица данной
квадратичной формы имеет вид:
 .
.
Найдем главные миноры
матрицы
![]() .
.
Следовательно, квадратичная форма – знакопеременная М1 не является точкой локального экстремума.
2)
![]() .
Матрица квадратичной формы:
.
Матрица квадратичной формы:
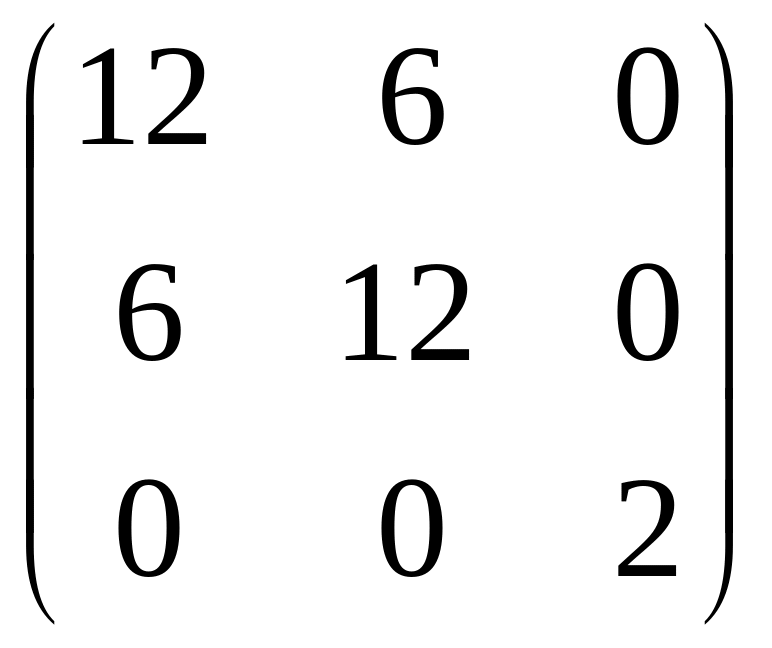 .
Главные миноры:
.
Главные миноры:
![]() .
.
Квадратичная форма
– положительно определенная, то есть
![]() и
и
![]() --
точка локального минимума.
--
точка локального минимума.
![]() .
.
3)
![]() .
.
Матрица квадратичной
формы:
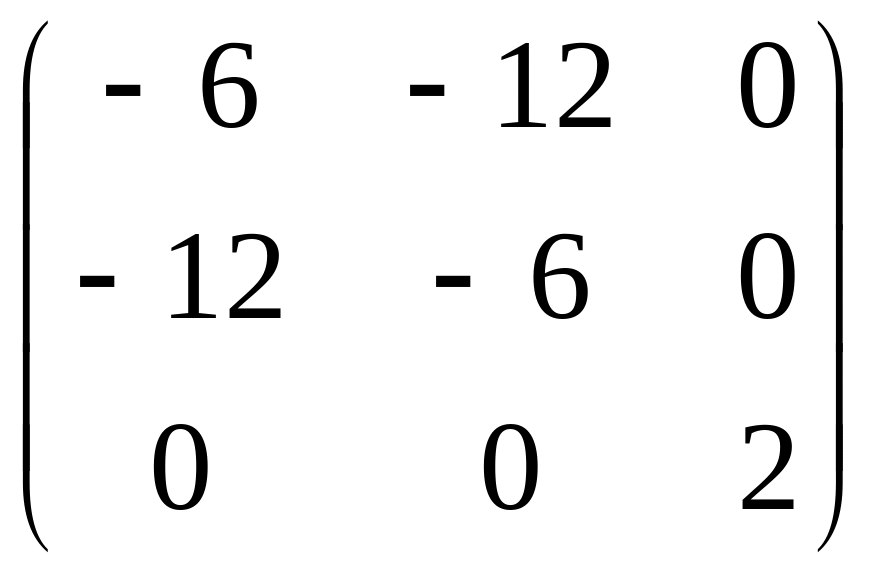 .
.
Главные миноры
матрицы:
![]() .
.
Следовательно, М3 не является точкой локального экстремума.
4) Аналогично, проверьте самостоятельно, что точка М4 не является точкой локального экстремума.
