Решение типовых примеров

Пример 5.2.1. Случайная величина Y имеет экспоненциальное распределение

.

а) Найти максимально правдоподобную оценку математического ожидания m этой случайной величины.

б) Найти статистические характеристики (математическое ожидание и дисперсию) этой оценки.

в) Определить, является ли оценка достаточной.

г) Определить, является ли оценка эффективной.

д) Найти информацию Фишера и по неравенству Рао-Кра­мера проверить сделанное заключение об эффективности оценки.

Решение. Запишем уравнение правдоподобия

Отсюда , т.е. максимально правдоподобная оценка математического ожидания равна наблюдаемому выборочному значению .

По формуле (5.2.4) находим математическое ожидание оценки .

Таким образом, оценка является несмещенной.

Дисперсию оценки вычисляем по формуле (5.2.5)

.

Для того чтобы определить, является ли оценка достаточной, сравним функцию правдоподобия с выражением (5.2.9).

Видим, что h(y)= 1, а функция зависит только от и . Функция правдоподобия выборки может быть представлена в форме (5.2.9), и оценка является достаточной.

Полученное ранее выражение сравним с выражением (5.2.10). Полагая и подставляя полученные нами выражения и m(x)=x, видим, что производная от логарифма функции правдоподобия может быть представлена в виде (5.2.10), и, следовательно, оценка максимального правдоподобия является эффективной.

Информацию Фишера находим по формуле (5.2.3)

Видим, что неравенство Рао-Крамера (5.2.8) обращается в равенство. Этого и следовало ожидать, так как мы уже показали, что оценка эффективна. Лучшей оценки, т.е. обладающей меньшей дисперсией при отсутствии систематической ошибки, не существует.

Пример 5.2.2. Система независимых случайных величин

распределена нормально с одинаковым среднеквадратическим отклонением и одинаковым, но неизвестным математическим ожиданием x.

а) Найти выражение для максимально правдоподобной оценки математического ожидания .

б) Найти смещение и дисперсию этой оценки.

в) Определить потенциальную точность оценки величины математического ожидания .

Решение. Функция правдоподобия выборки равна

Запишем уравнение правдоподобия и преобразуем его к удобному виду

Решением уравнения является значение

.

Таким образом, максимально правдоподобная оценка математического ожидания х равна выборочному среднему.

По формуле (5.2.4) найдем математическое ожидание самой оценки

так как математическое ожидание суммы случайных величин равно сумме математических ожиданий. Таким образом, смещение оценки равно нулю.

Дисперсия оценки может быть найдена непосредственно по формуле (5.2.6) либо же следующим, более простым способом. Величина является суммой n независимых случайных величин, причем дисперсия каждого из слагаемых равна . Тогда дисперсия этой суммы равна , и тогда дисперсия оценки

Вычисление информации Фишера, содержащейся в выборке, удобно произвести с использованием свойства аддитивности

,

где

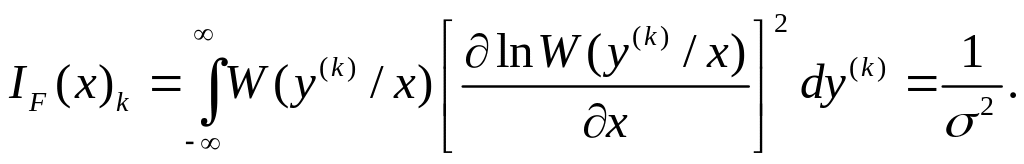
Неравенство Рао-Крамера обращается в равенство, и, следовательно, найденная нами оценка достаточна и эффективна.

Пример 5.2.3. На интервале времени (0,Т) принимается сигнал

где – сигнал известной формы, но с неизвестной задержкой мкс,

– белый нормальный шум со спектральной плотностью .

Найти потенциальную точность оценки временной задержки .

Решение. По определению (5.2.2) информация Фишера численно равна

где – средняя информация для различения в пользу гипотезы Н₁ (передан сигнал ) против гипотезы Н₂ (передан сигнал ). Эту величину мы вычисляли в примере 5.1.3, где получили

.

Дифференцируем эту функцию дважды по :

,

.

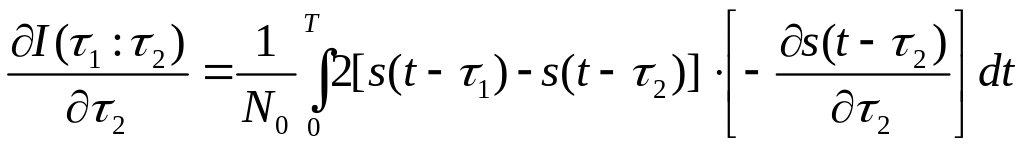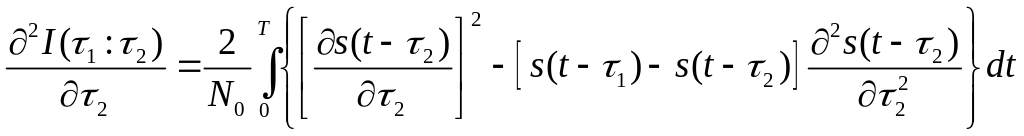Полагаем далее и получаем

Применяя неравенство Рао-Крамера, получим для дисперсии несмещенной оценки параметра

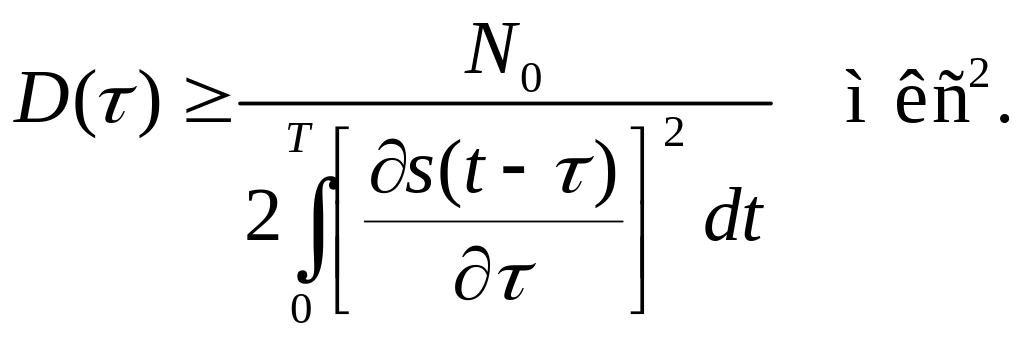
ЗАДАЧИ

5.2.1. Случайная величина распределена нормально с известным средним значением и неизвестной дисперсией. Найти потенциальную точность несмещенной оценки дисперсии.

5.2.2. Решить задачу 5.2.1 в предположении, что имеется n

независимых реализаций случайной величины.

5.2.3. Случайная величина распределена равномерно на

интервале известной длины, но с неизвестным средним значением . Показать, почему в задаче оценки параметра не может быть использовано неравенство Крамера-Рао.

5.2.4. Найти потенциальную точность оценки направления

на источник при помощи двухантенного фазового пеленгатора, если разность фаз на входе фазометра равна

,

где – база пеленгатора,

-длина волны,

— угол между нормалью к плоскости антенн и направлением на источник.

Ошибка измерения разности фаз распределена нормально с нулевым средним и среднеквадратическим отклонением 2°.

5.2.5. Найти потенциальную точность оценки допплеровского сдвига частоты од узкополосного сигнала известной формы

.

Шум на входе измерителя – белый аддитивный нормальный со спектральной плотностью N₀.

5.2.6. Найти потенциальную точность оценки амплитуды А прямоугольного импульса длительности , принимаемого на фоне аддитивного белого нормального шума со спектральной плотностью N₀.

5.2.7. Найти потенциальную точность оценки начальной фазы прямоугольного радиоимпульса длительности

, ,

принимаемого на фоне аддитивного белого нормального шума со спектральной плотностью N₀.

5.2.8. Производитcя однократное бросание монеты неправильной формы:

а) найти максимально правдоподобную оценку вероятности р выпадения герба;

б) вычислить смещениё и дисперсию такой оценки, предполагая, что истинное значение р = 0,4;

в) определять, является ли оценка эффективной.

5.2.9. Решить задачу 5.2.8. для случая, когда производится n независимых бросаний монеты.

5.2.10. Производится однократное бросание шестигранной игральной кости неправильной формы. Пусть -вероятности выпадения соответствующего количества очков. Если выпало очков, считают, что , а . Является ли такая оценка эффективной?

5.2.11 . Система n случайных величин имеет нормальное распределение, причем вектор-столбец средних значений S(х) и корреляционная матрица R(х) известным образом зависят от неизвестного параметра . Вычислить информацию Фишера о параметре .

5.2.12. Решить задачу 5.2.11 для случаев, когда от зависит только S(х) или только R(х).

5.2.13. В условиях задачи 5.1.11 вычислить информацию Фишера о параметре , считая его непрерывным.

5.2.14. Случайная величина распределена равномерно на интервале длиной 10 м, но ее среднее значение неизвестно. Является ли оценка оценкой максимального правдоподобия?