
- •Розділ і Невизначений інтеграл
- •§1. Первісна для функції
- •§2. Невизначений інтеграл
- •§3. Основні прийоми інтегрування
- •Результатом застосування формули (3.1) двічі є
- •Аналогічно допускають повне обчислення і інтеграли виду
- •Навпаки, не можуть бути представлені через елементарні функції інтеграли
- •§4 Техніка невизначеного інтегрування
- •Розглянемо спочатку інтегрування простих раціональних функцій. Такими є:
- •Таким чином,
- •Розглянемо окремо інтеграл
- •Поділимо на нього чисельник, після чого одержимо
- •Так, функції
- •2. Деякі інтеграли, які раціоналізуються
- •Тому інтеграл
- •3. Інтеграли від деяких ірраціональних виразів Розглянемо інтеграл виду
- •Але інтеграли виду
- •Інтеграл
- •Але можна діяти і інакше, якщо зробити підстановку
- •§5. Інтеграл від диференціального бінома
- •§ 6. Мішані типові задачі на інтегрування
Інтеграл
![]()
аналогічно зводиться до такого ж типу підстановкою
 .
.
Але можна діяти і інакше, якщо зробити підстановку
![]()
і
![]() .
.
Приклад 4.11.
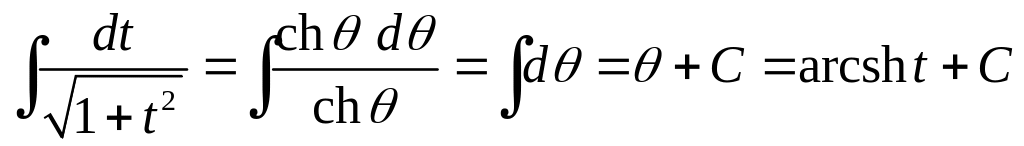 ,
,
де
![]() функція,
обернена по відношенню до
функція,
обернена по відношенню до
![]() .
У той же час із таблиці інтегралів маємо
.
У той же час із таблиці інтегралів маємо
 .
Різні результати (підкреслимо ще раз),
одержані різними підстановками, не
повинні нас приводити до тупикової
ситуації: результати, як свідчить теорія,
будуть відрізнятися на сталу.
.
Різні результати (підкреслимо ще раз),
одержані різними підстановками, не
повинні нас приводити до тупикової
ситуації: результати, як свідчить теорія,
будуть відрізнятися на сталу.
І тепер, у випадку
![]()
можна
запропонувати, наприклад, таку підстановку
![]() (а можна і
(а можна і
![]() або
або
![]() ).
).
Приклад 4.12. Обчислити
 .
.
Варіант 1:
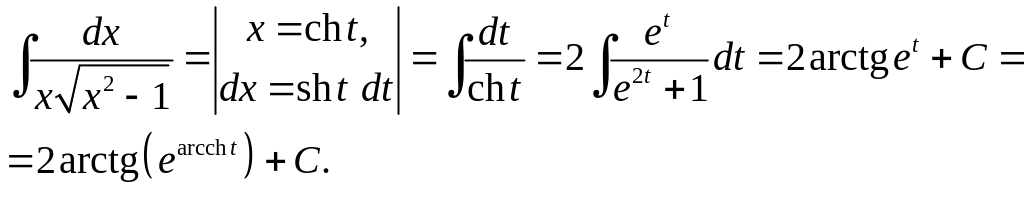
Варіант 2:
 .
.
Варіант 3:
 .
.
Варіант 4:
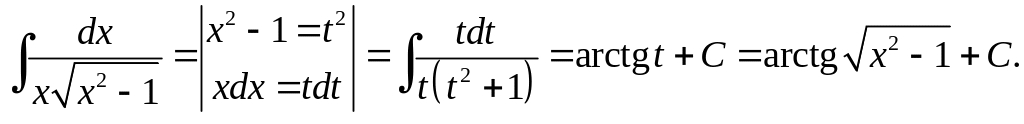
Зауваження. Інтеграл
можна раціоналізувати зразу підстановками Ейлера. Ми не будемо детально розписувати, але вкажемо ці підстановки
1) якщо
![]() ,
то покладемо
,
то покладемо
![]() ;
;
2) якщо
![]() ,
то
,
то
![]() ;
;
3) якщо
![]() ,
то розглянемо два випадки:
,
то розглянемо два випадки:
3*)
![]() ,
безумовно,
повинно бути додатнім і
,
безумовно,
повинно бути додатнім і
![]() ;
;
3**)![]() ,
тоді
,
тоді
![]() .
.
Приклад 4.13. Обчислити інтеграл
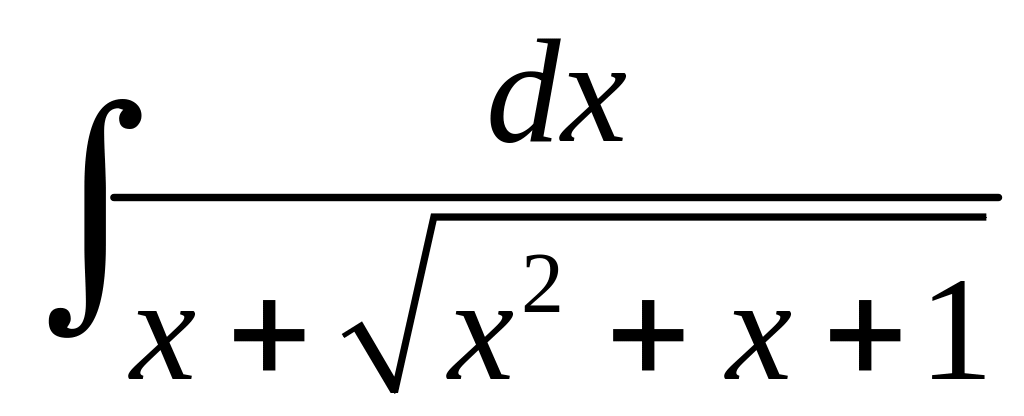 .
.
тут
![]() .
Візьмемо, наприклад, знак "".
Тоді
.
Візьмемо, наприклад, знак "".
Тоді
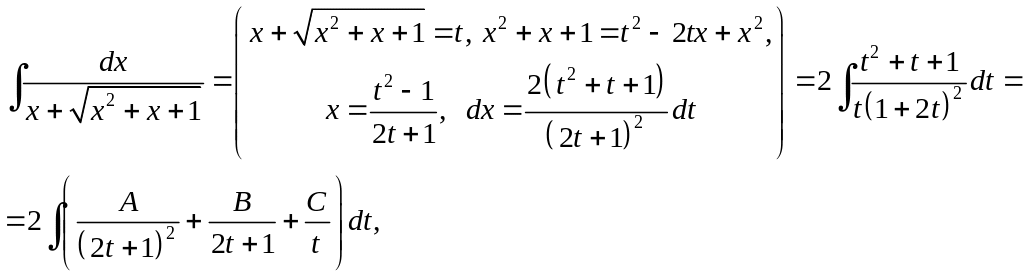
де
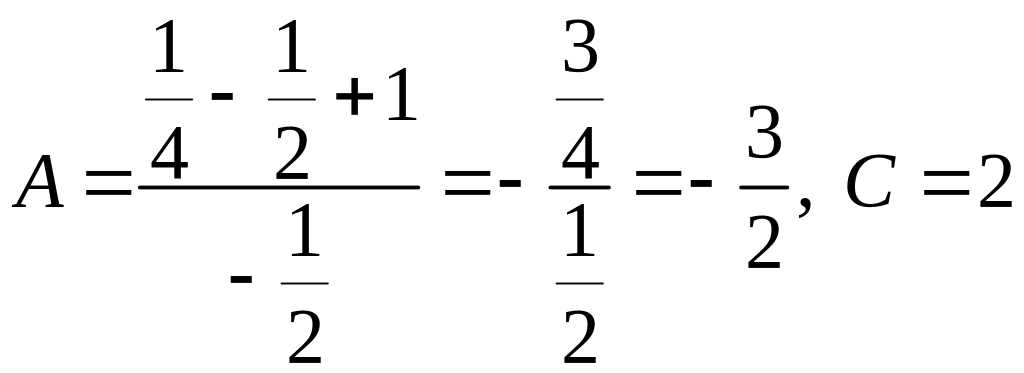 .
Неважко перевірити, що
.
Неважко перевірити, що
![]() і
і
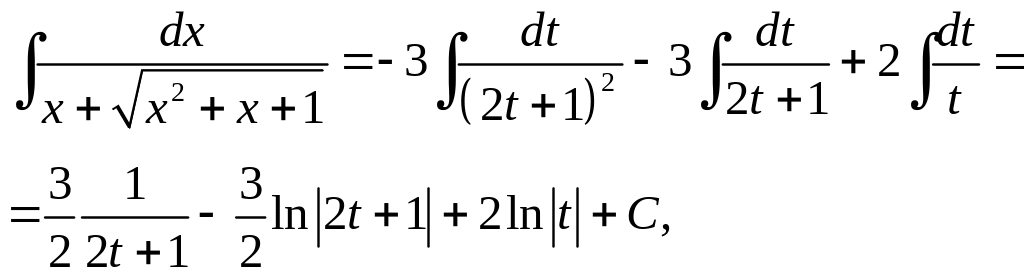
де
![]() .
.
§5. Інтеграл від диференціального бінома
Диференціальним біномом називають вираз
![]() .
.
1. Нехай
![]() .
У цьому випадку диференціальний біном
є ірраціональність виду
.
У цьому випадку диференціальний біном
є ірраціональність виду
![]() ,
де
,
де
![]() найменше
загальне кратне знаменників раціональних
чисел
найменше
загальне кратне знаменників раціональних
чисел
![]() .
А як відомо, інтеграл раціоналізується
підстановкою
.
А як відомо, інтеграл раціоналізується
підстановкою
![]() .
.
2. Нехай
![]() .
Покладемо
.
Покладемо
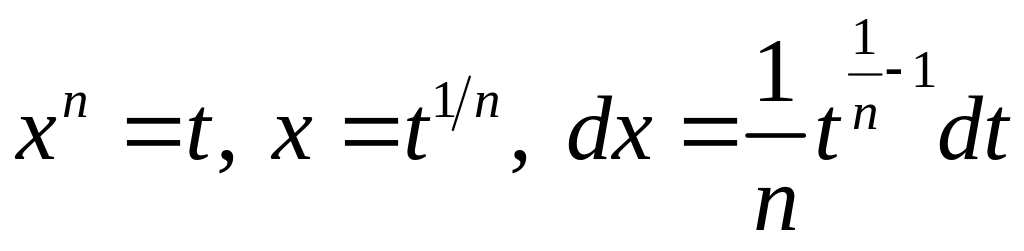 ,
тоді
,
тоді
 (5.1)
(5.1)
Якщо
![]() ,
маємо
,
маємо
![]() .
.
Як відомо
(4.4), одержаний інтеграл раціоналізується
підстановкою
![]() ,
де
,
де
![]() знаменник
знаменник
![]() .
.
3. Нехай
![]() ,
тоді перепишемо інтеграл (5.1) інакше
,
тоді перепишемо інтеграл (5.1) інакше
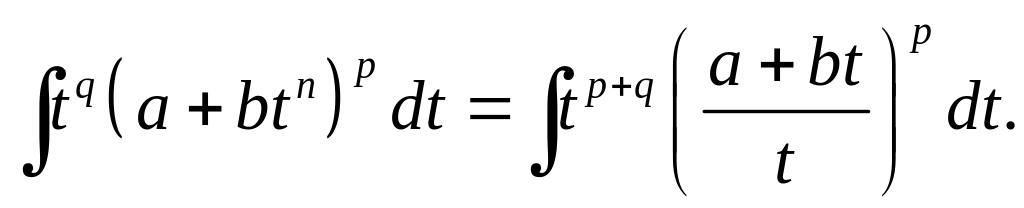
Якщо
![]() ,
то одержаний інтеграл типу (4.3) і
підстановкою
,
то одержаний інтеграл типу (4.3) і
підстановкою
 ,
де
знаменник
,
він раціоналізується.
,
де
знаменник
,
він раціоналізується.
Одержані результати остаточно перефразуємо наступним чином:
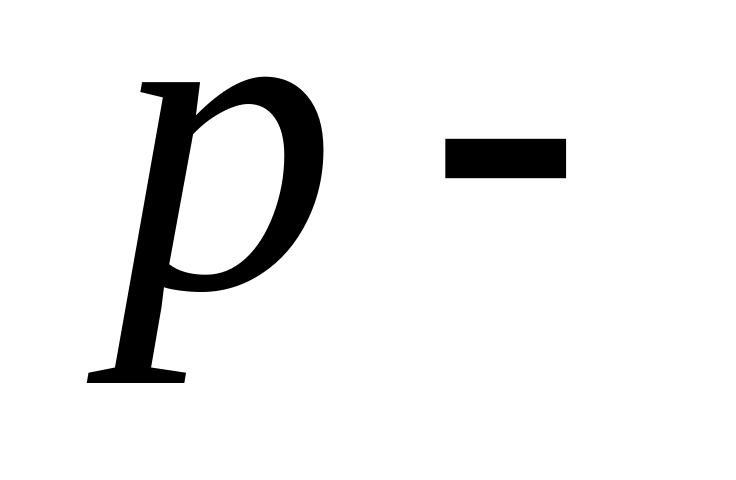 ціле,
тоді підстановка
ціле,
тоді підстановка
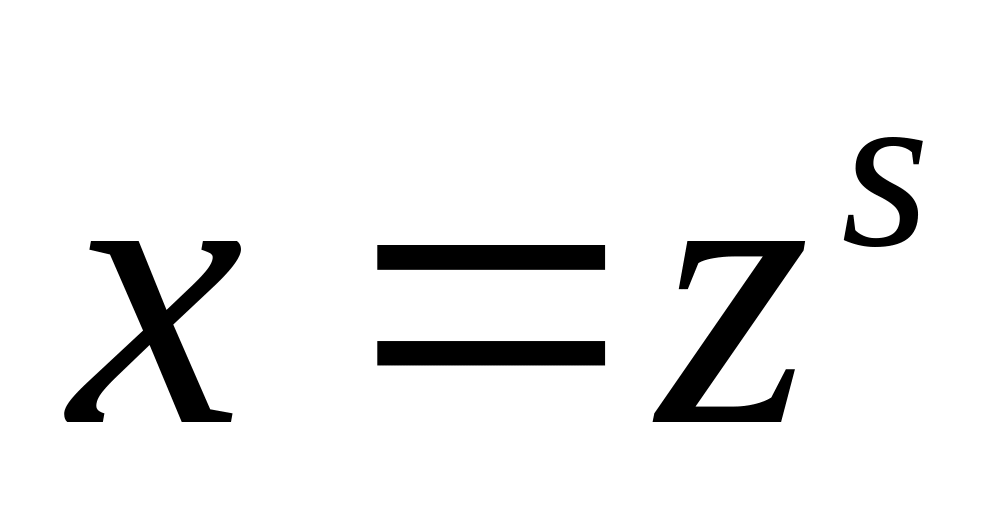 де
загальний
знаменник дробів
де
загальний
знаменник дробів
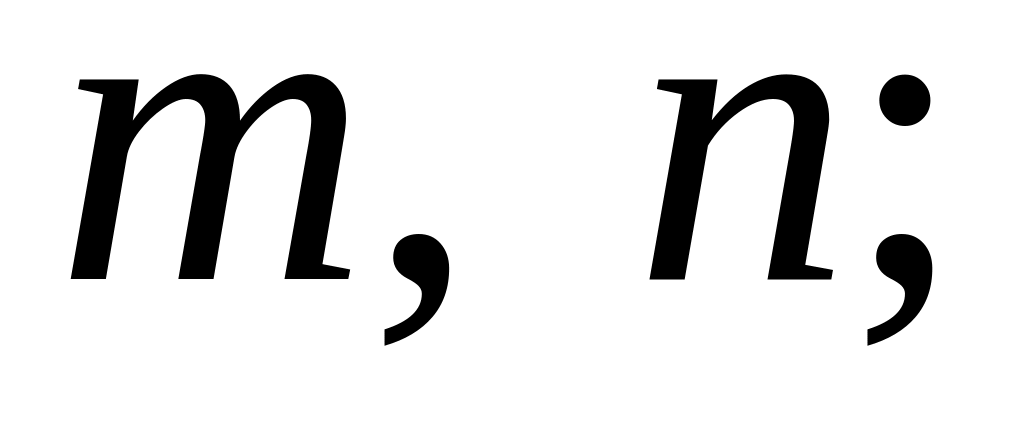
не ціле, але
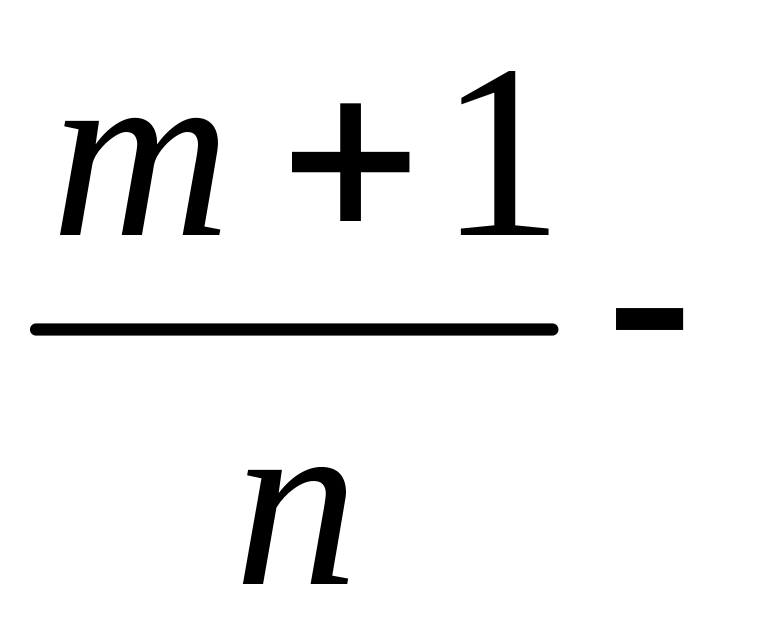 ціле,
тоді підстановка
ціле,
тоді підстановка
 ,
де
знаменник
;
,
де
знаменник
;не ціле, але
 ціле,
тоді підстановка
ціле,
тоді підстановка
 ,
де
знаменник
.
,
де
знаменник
.
Теорема
(Чебишева П.Л.) Інтеграл від диференціального
бінома виражається в елементарних
функціях тільки в трьох випадках:
![]() ціле,
ціле,
![]() ціле,
ціле,
![]() ціле.
Якщо жодна з умов
ціле.
Якщо жодна з умов
![]() не виконується, то інтеграл знайти в
класі елементарних функцій неможливо.
не виконується, то інтеграл знайти в
класі елементарних функцій неможливо.
Приклад 5.1. Обчислити інтеграл
 .
.
Тут
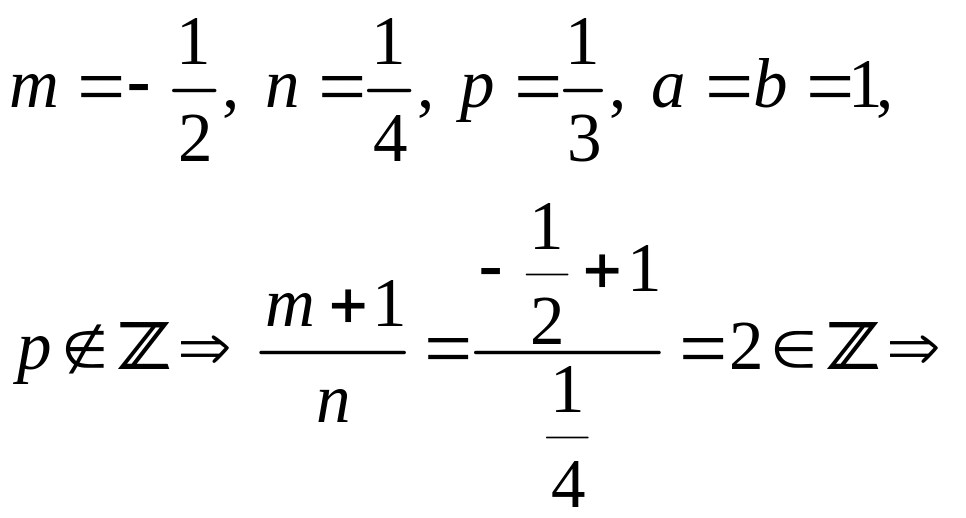
зробимо
підстановку
![]() ,
тоді
,
тоді

Приклад 5.2. Обчислити інтеграл
![]()
Тут
![]() інтеграл
неможливо одержати як композицію
елементарних функцій.
інтеграл
неможливо одержати як композицію
елементарних функцій.
Приклад 5.3. Обчислити інтеграл
![]()
Тут
![]() .
Маємо третій випадок, а тому зробимо
підстановку
.
Маємо третій випадок, а тому зробимо
підстановку

Отже,

Раціональніше
обчислити цей інтеграл інтегруванням
частинами, або підстановкою
![]() .
.
У попередніх параграфах методи інтегрування супроводжувались відповідними прикладами. Нижче наведемо інтеграли, де студент може самостійно вибрати той чи інший метод для обчислення інтеграла. Тим більше, що ці приклади детально розібрані і вказані найраціональніші методи обчислення або відповідна підстановка.
§ 6. Мішані типові задачі на інтегрування
Обчислити інтеграли:
Приклад 6.1.
![]() .
.
Розв'язання. Достатньо перенести ірраціональність в чисельник
![]()
(дивись властивість і таблицю).
Приклад 6.2.
![]() .
.
Розв'язання.

(дивись властивість і таблицю).
Приклад 6.3.
 .
.
Розв'язання.
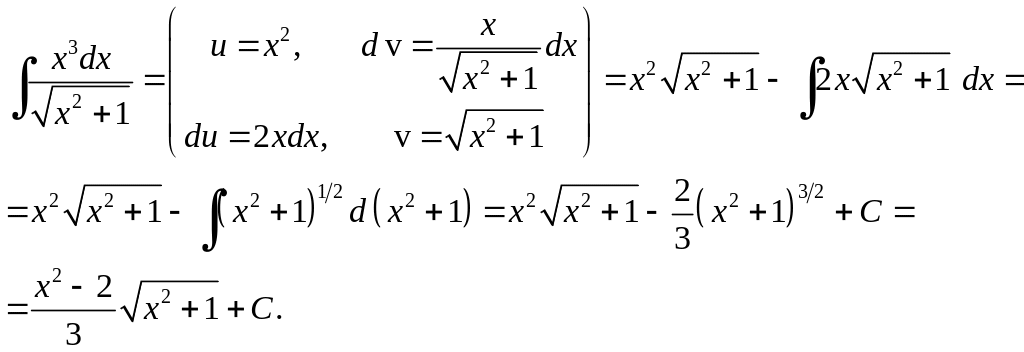
Приклад 6.4.
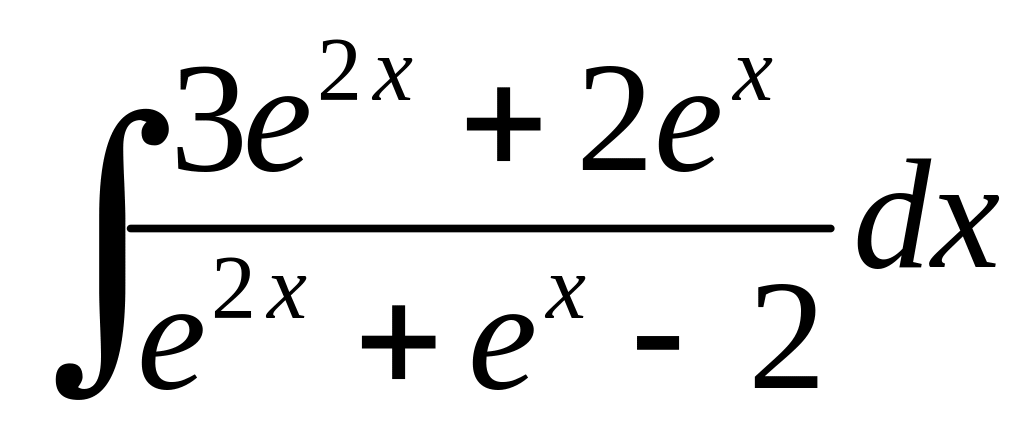 .
.
Розв'язання.
Підінтегральна функція раціональна
відносно
![]()
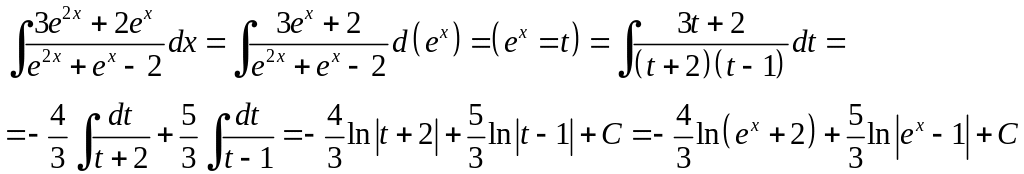
(тут було
враховано, що
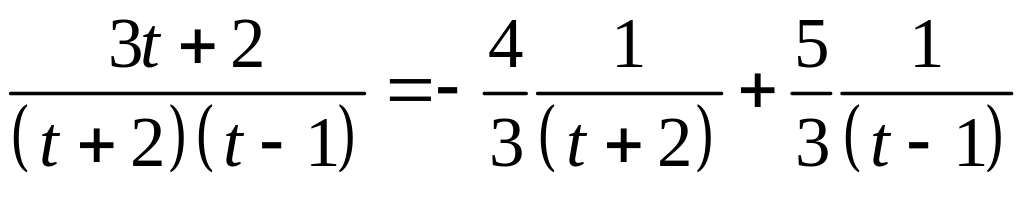 ).
).
Приклад 6.5.
![]() .
.
Розв'язання.
Підінтегральний вираз раціонально
залежить від
![]()
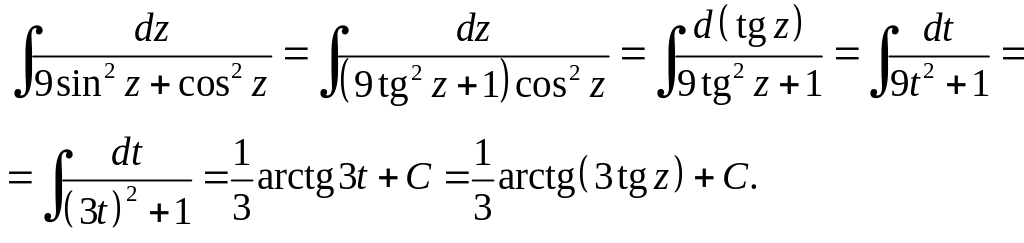
Приклад 6.6.
 .
.
Розв'язання. Підінтегральна функція є неправильним раціональним дробом. Виділимо цілу частину
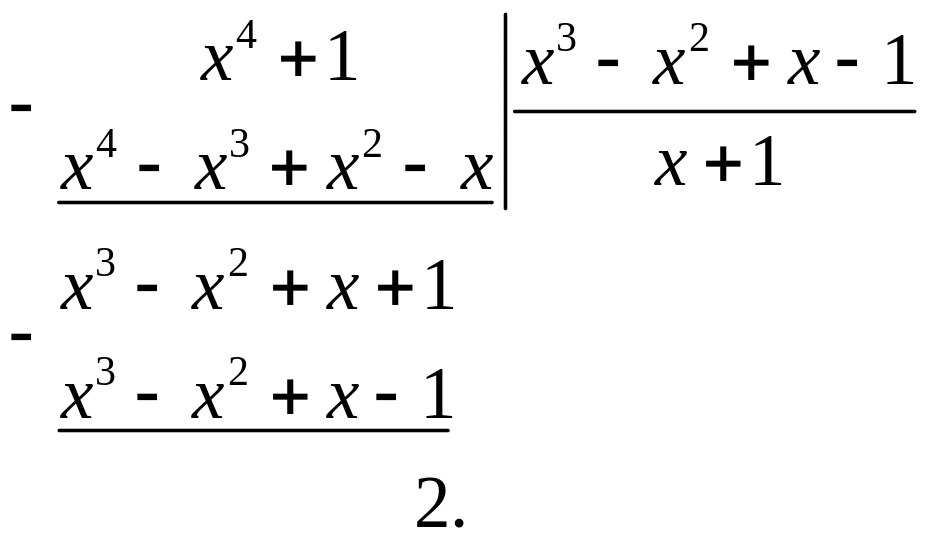
Таким чином,
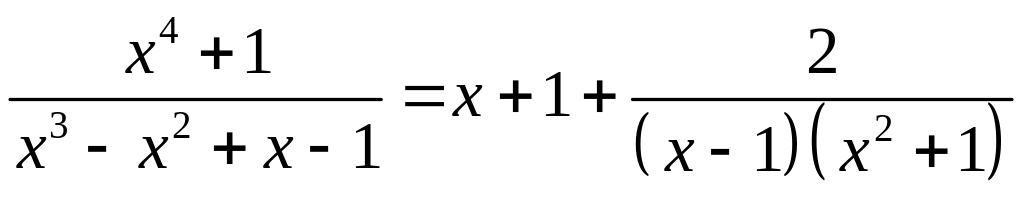 .
.
Розкладемо
дріб
 на суму двох дробів першого та третього
типу:
на суму двох дробів першого та третього
типу:

Прирівнюючи коефіцієнти при однакових степенях в обох частинах останньої рівності, будемо мати
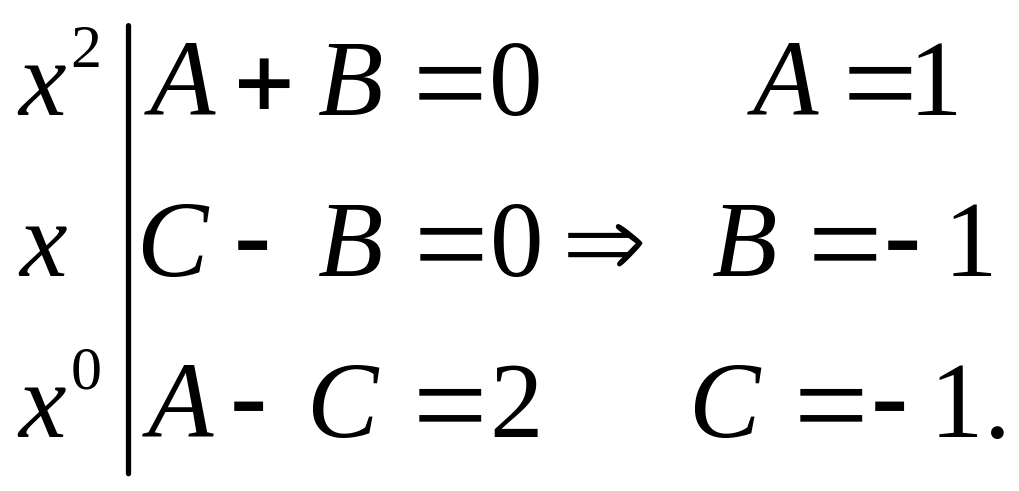
Таким чином,
 .
.
Остаточно маємо:

Приклад 6.7.
 .
.
Розв'язання.
Щоб звільнитися від ірраціональності
в чисельнику, помножимо чисельник і
знаменник на
![]()
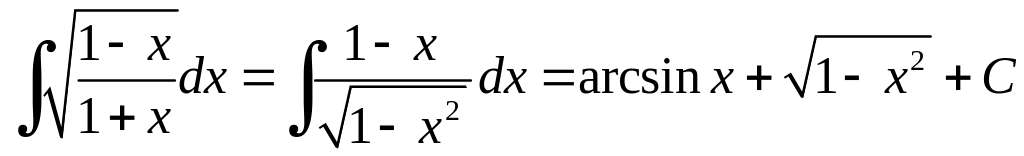 .
.
Приклад 6.8.
 .
.
Розв'язання.
Використаємо підстановку
![]() ,
,
![]() і
і
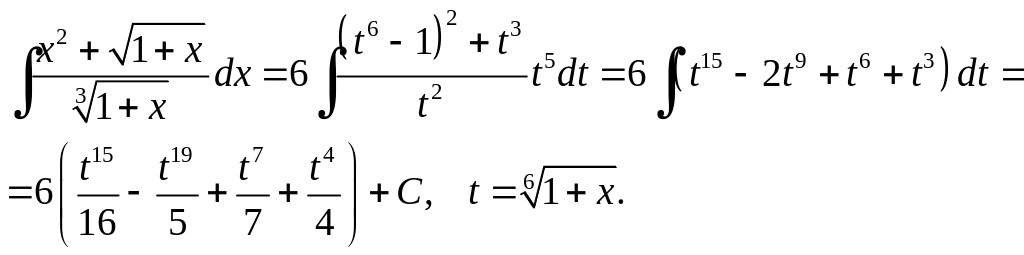
Приклад 6.9.
![]() .
.
Розв'язання. Застосуємо метод інтегрування частинами.

Приклад 6.10.
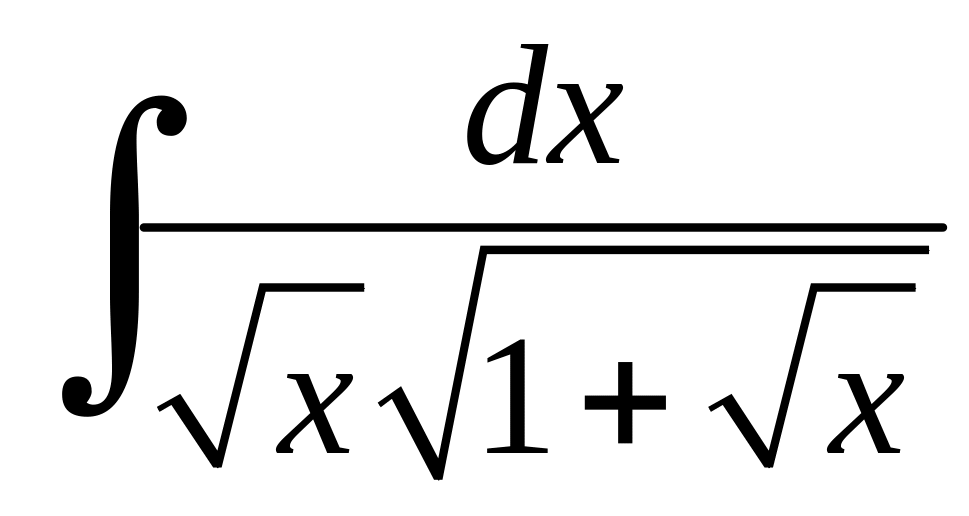
Розв'язання.
Оскільки
![]() ,
то одержуємо
,
то одержуємо
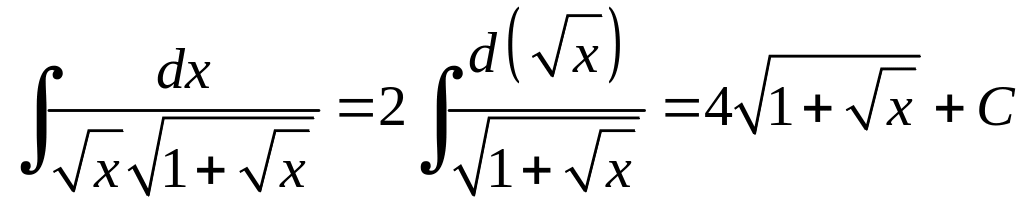 .
.
Приклад 6.11.
 .
.
Розв'язання.
Обираємо підстановку
![]()
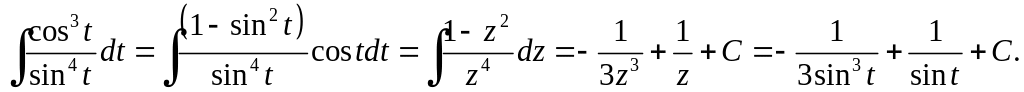
Приклад 6.12.
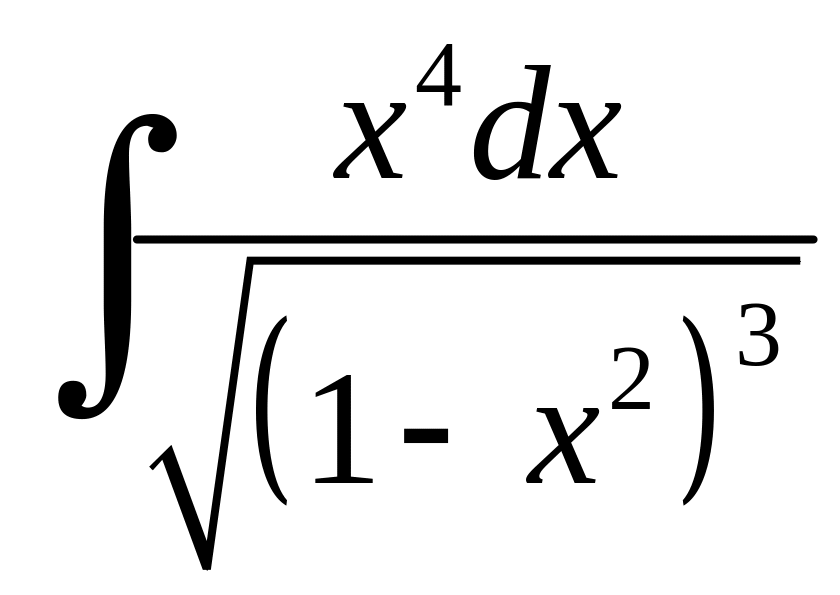 .
.
Розв'язання.
Підінтегральна функція має вид
![]() ,
тому доцільно використати підстановку
,
тому доцільно використати підстановку
![]() ,
,
![]() .
.
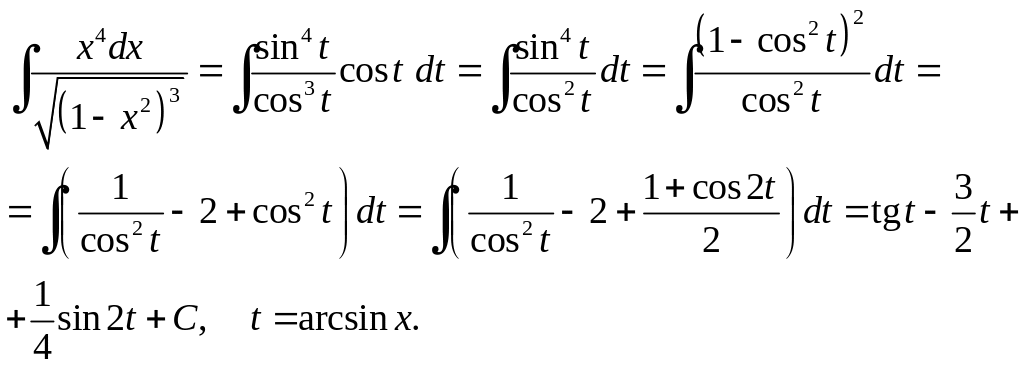
Приклад 6.13.
 .
.
Розв'язання.
Підінтегральна функція має вид
![]() ,
тому доцільно було б скористатися
підстановкою
,
тому доцільно було б скористатися
підстановкою
![]() ,
але ми поступимо інакше:
,
але ми поступимо інакше:
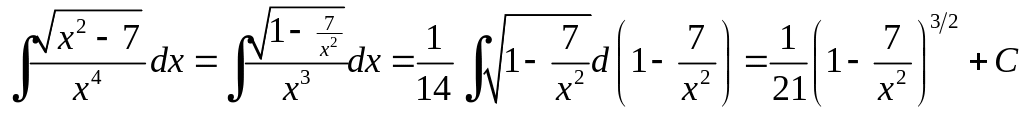
Приклад 6.14.
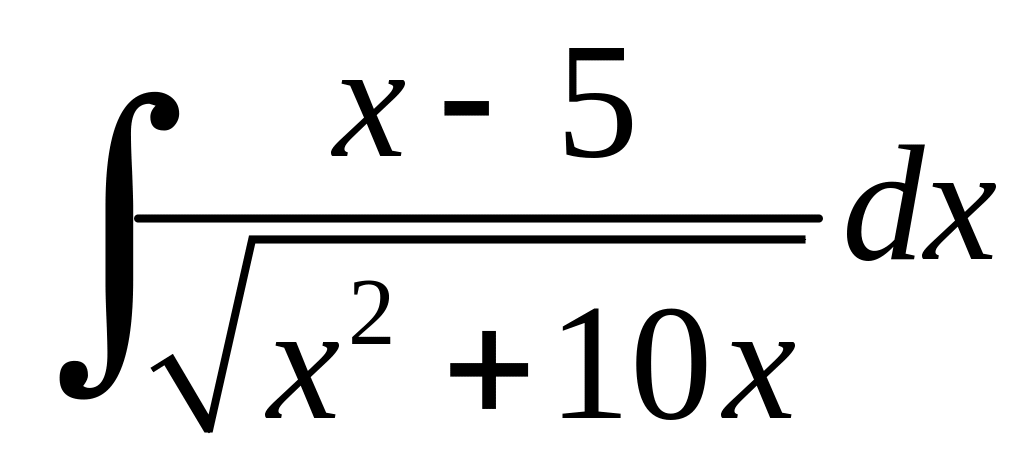 .
.
Розв'язання. Виділимо повний квадрат у квадратному тричлені
![]()
Тоді
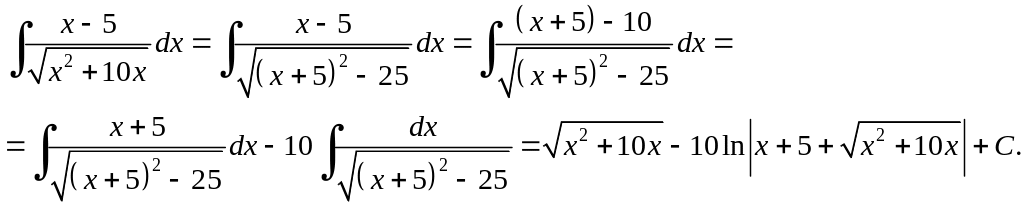
Приклад 6.15.
 .
.
Розв'язання.
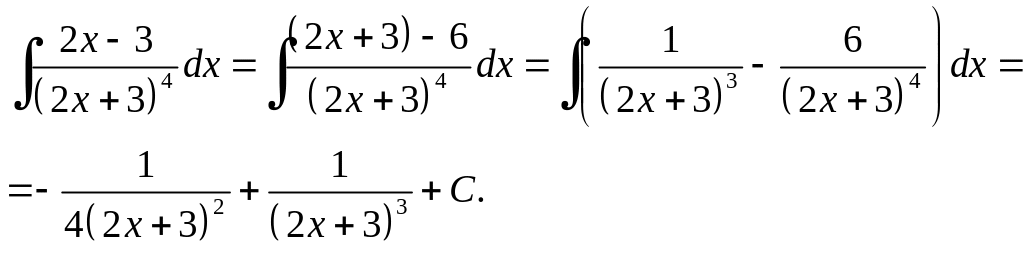
Приклад 6.16.
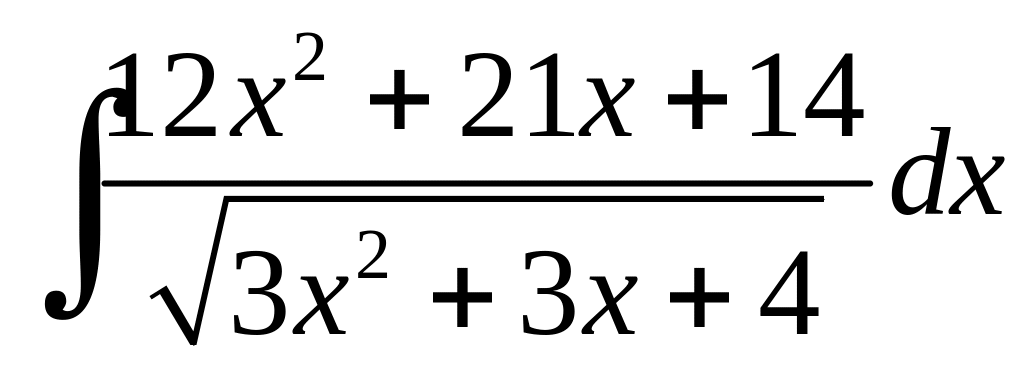 .
.
Розв'язання.
Інтеграли типу
 можна обчислити за формулою
можна обчислити за формулою
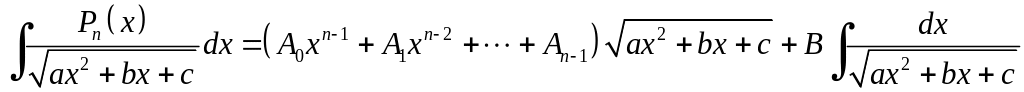 ,
,
де
![]() сталі,
визначені наступним чином. Продиференціюємо
обидві частини цієї рівності. Якщо після
цього привести до загального знаменника,
то із рівності чисельників одержимо
систему відносно
сталі,
визначені наступним чином. Продиференціюємо
обидві частини цієї рівності. Якщо після
цього привести до загального знаменника,
то із рівності чисельників одержимо
систему відносно
![]() .
.
Подібним чином можна обчислити і інтеграли
![]() .
.
Зрозуміло, що в цьому випадку достатньо ірраціональність перенести до знаменника.
Таким чином,
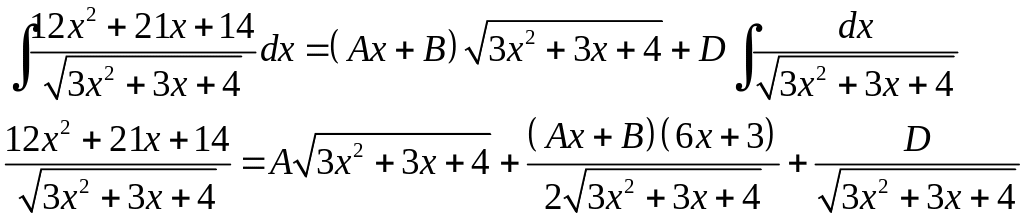
Прирівнюючи чисельники, одержимо
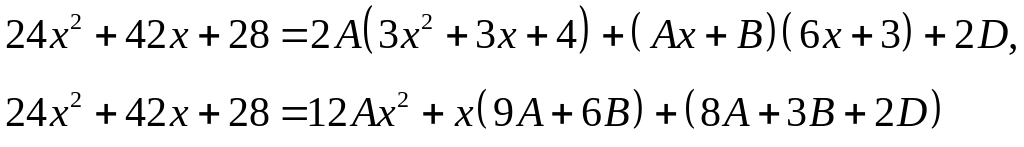
Прирівнюючи коефіцієнти при однакових степенях в обох частинах останньої рівності, маємо

Остаточно маємо
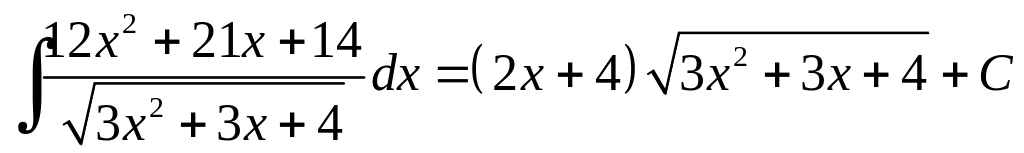
Приклад 6. 17

Розв'язання.
Зробимо підстановку
![]() .
Маємо
.
Маємо
![]() .
Отже
.
Отже
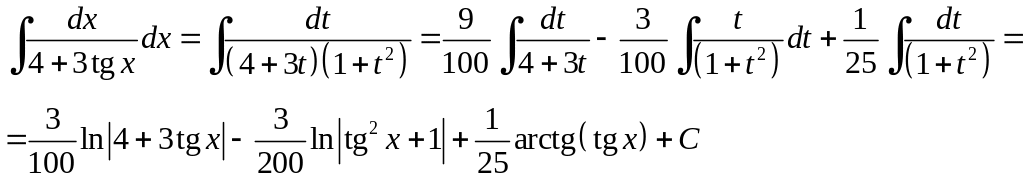
Тут було враховано, що

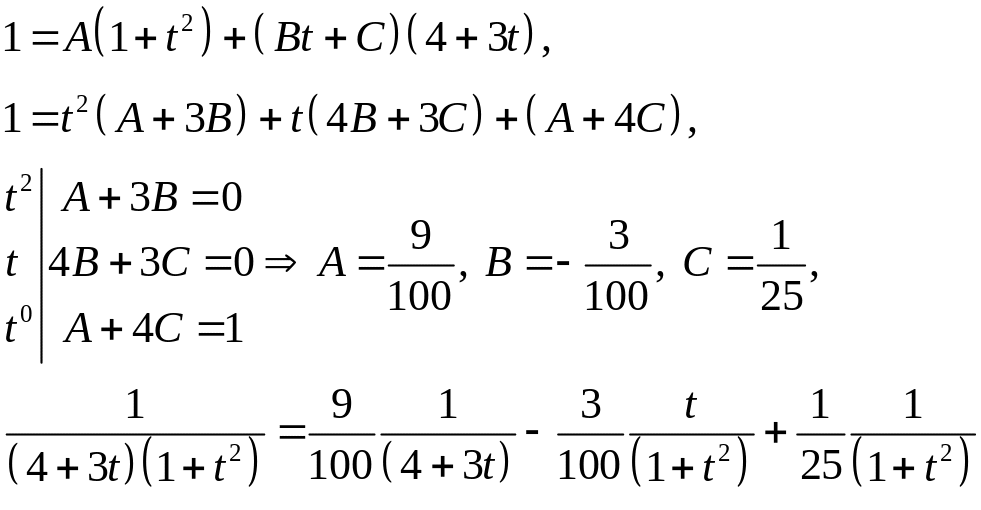
Вкажемо інші, на наш погляд більш раціональні варіанти
Варіант
1:
Можна використати універсальну
тригонометричну підстановку
![]() .
Тоді
.
Тоді
![]() .
Маємо
.
Маємо

Варіант 2: підінтегральну функцію перетворимо наступним чином

тоді
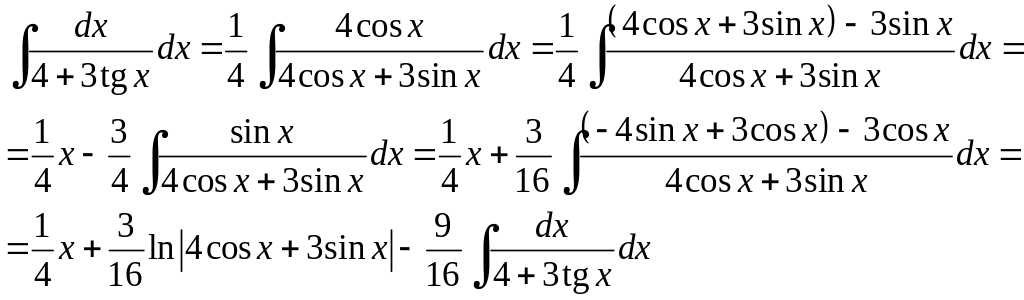
Отже остаточно маємо
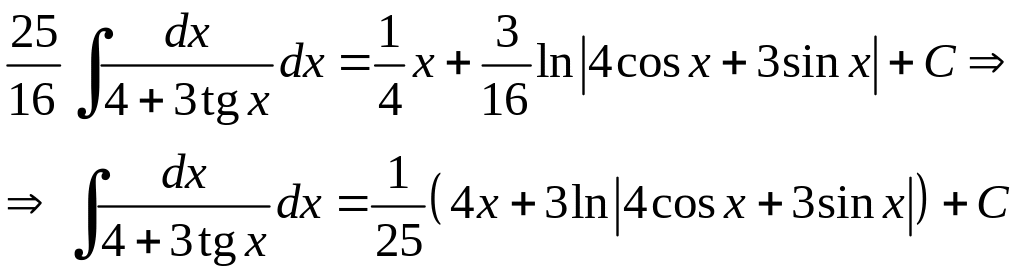
Приклад 6.18

Розв'язання.
Підінтегральна функція має вид
,
тому доцільно було б використати
підстановку
![]() ,
але можна і інакше
,
але можна і інакше
 .
.
Приклад 6.19.
![]() .
.
Розв'язання. Застосуємо метод інтегрування частинами.

Приклад 6.20.
![]() .
.
Розв'язання. Спростимо вираз у знаменнику підінтегральної функції
![]() .
.
Отже
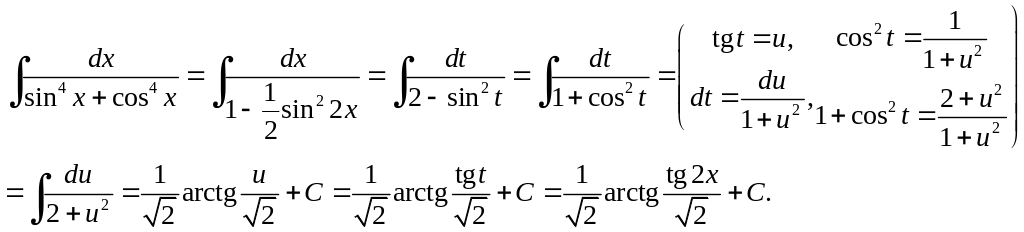
Приклад 6.21.
 .
.
Розв'язання.

Приклад 6.22.
![]() .
.
Розв'язання.
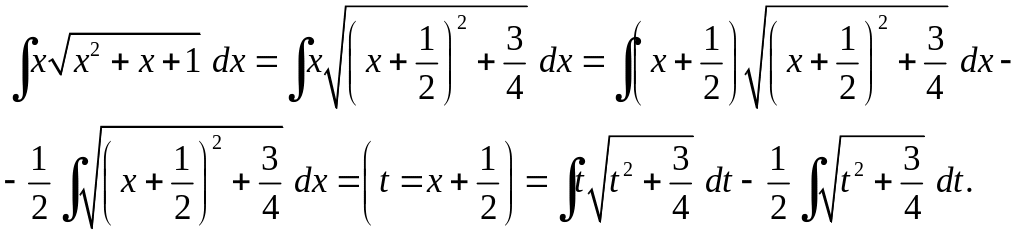
Тепер для обчислення першого інтегралу скористаємося методом інтегрування частинами, а другого методом заміни змінної:
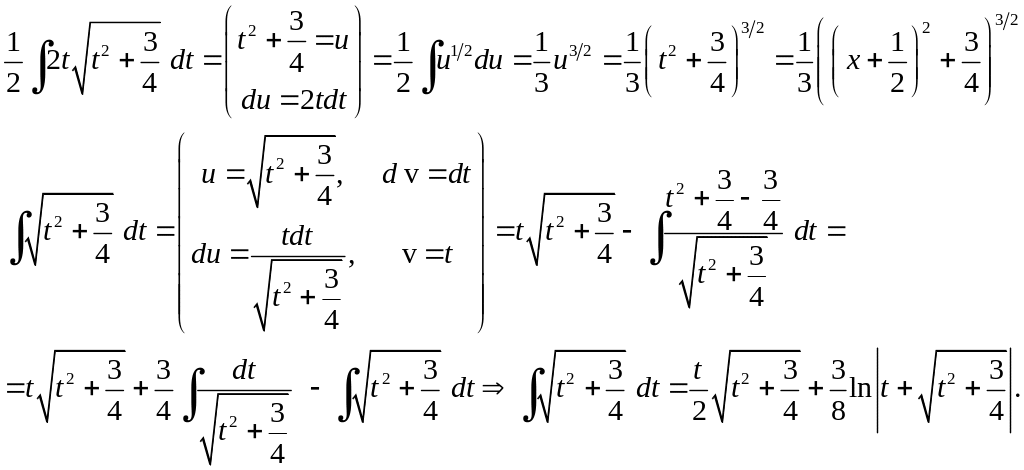
Остаточно маємо
 .
.
Приклад 6. 23.
![]() .
.
Розв'язання.

Зауваження. Якщо Вам хватило терпіння дочитати цей розділ, то Ви зрозуміли, що інтегрування це мистецтво, яким треба оволодіти досить добре, тим більше, що багато інтегралів, яких потребує практика, носять назву „неберущихся”. Окрім наведених в цьому розділі, такими є еліптичні інтеграли, до них зводять задачі знаходження довжини дуги еліпсу, звідки і виникла ця назва. Про них і їм подібних поговоримо пізніше в наступних розділах.
Приведемо два приклада на застосування невизначеного інтегралу в курсі алгебри.
Приклад 6.24. Спростити вираз
![]() .
.
Розв'язання. Маємо
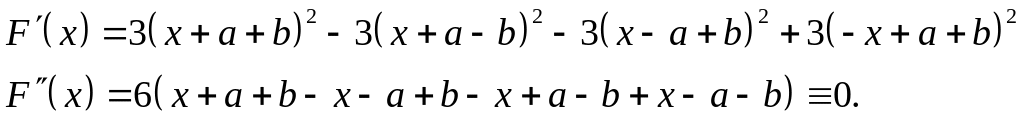
Звідки
![]() .
Зокрема, коли
маємо
.
Зокрема, коли
маємо
![]() .
.
Таким
чином,
![]() ,
а тому
,
а тому
![]() .
Покладемо
,
тоді
.
Покладемо
,
тоді
![]() ,
звідки
,
звідки
![]() .
Отже
.
Отже
![]()
Приклад 6.25. Довести тотожність
![]() .
.
Розв'язання. Нехай
![]() .
.
Тоді
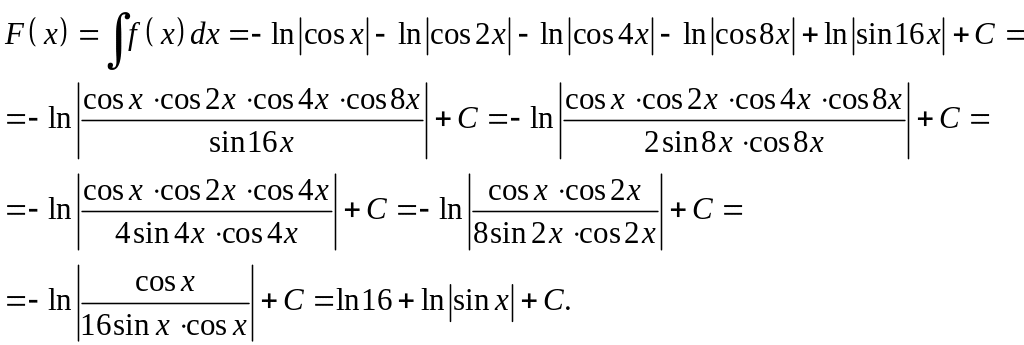
Знайдемо
похідну функції
:
![]() ,
що і потрібно було довести.
,
що і потрібно було довести.
