Figure 4 Flat Earth Reference Coordinate system

Inertial Navigation Unit

The inertial navigation unit (INU) of an aircraft is designed to maintain a local inertial reference frame. However, the origin of this reference frame is centered within the INU which is not usually located at the aircraft center of gravity. Therefore, during dynamic manoeuvres, the INU orientation, acceleration and velocity data must be corrected for fuselage bending and the offset from the center of gravity in order to determine the actual values in the true inertial reference frame. Additionally, the INU coordinate system may not be aligned with the inertial (flat-Earth) frame defined above.

Figure 5 F-16 Inertial Navigation Unit Coordinate System

COORDINATE SYSTEM TRANSFORMATION

With each of the aircraft coordinate systems defined, we can now develop the transformations between each system.

BODY-FIXED FORM STABILITY

The transformation to the body-fixed reference frame from the stability includes a single Rotation about the y_s – axis through the angle of attack, α, as shown in Fig. 6.

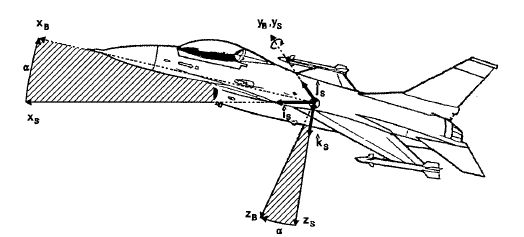
Figure 6 Stability to Body-Fixed Coordinate System transformation through the Angle of Attack, α

To transform expressed in the stability coordinates into body coordinates:

where

To transform defined in body-fixed coordinated to stability coordinates:

where

BODY-FIXED FROM INERTIAL

The transformation to the body-fixed reference frame from the inertial (flat Earth) reference frame is accomplished by three rotations through the angles ψ, θ, Φ, as shown in Fig.7. These angles are called Euler angles. The three rotations are not commutative, that is, they must be in the specified order to achieve the desired aircraft orientation.

Figure 7 Inertial to Body fixed Coordinate System Transformation through Euler angles

The first rotation is about the Z_I –axis through the yaw or heading angle, ψ, to the first intermediate coordinate system x₁, y₁, z₁, as shown in Figure 8. Thus, to transform a vector defined in the inertial reference frame into coordinates of the first intermediate frame:

, where

(1)

Figure 8 Inertial 1^st Intermidiate Coordinate System ransformation through the Heading Angle, ψ

The second rotation is about the y₁ – axis through the pitch angle, θ, to the second intermediate coordinate system x₂,y₂,z₂, as shown in Fig. 9. Defining in terms of this system:

, where

(2)

Figure 9 1^st to 2^nd Intermediate Coordinate System Transformation through the Pitch Angle, θ

The final third rotation is about the x₂- axis through the roll angle, Φ, to the body –fixed coordinate system (Fig.10). Defining in terms of the body system:

, where

(3)

Figure 10 3^rd Intermediate to Body-Fixed Coordinate System Transformation through the Roll angle, Φ

Now, to perform the entire transformation to the body-fixed coordinate system from the inertial, we simply multiply the rotation matrices (eq. 3, 2, 1) to obtain the desired transformation matrix:

where

Note: c=co sans s=sin.

Because they are orthogonal, each of the martices defined above in the equations have the unique property that the transpose of the matrix is equal to the inverse.

.

Thus, if we wish to transform a vector expressed in body-fixed coordinates into the inertial frame:

WIND FROM STABILITY

The transformation to the wind reference frame from the stability includes a single rotation through the angle of sideslip, β, as shown in Fig. 11. To transform expressed in the stability coordinates into wind coordinates:

where

.

Figure 11Stability to Wind Coordinate System Transformation through the Angle of Sideslip, β

To transform defined in wind coordinates to stability coordinates:

and

WIND FROM BODY-FIXED

The transformation to wind coordinates from the body-fixed system includes the two rotations through α and β as shown previously in Figure 3. To transform expressed in body coordinates into wind coordinates:

where

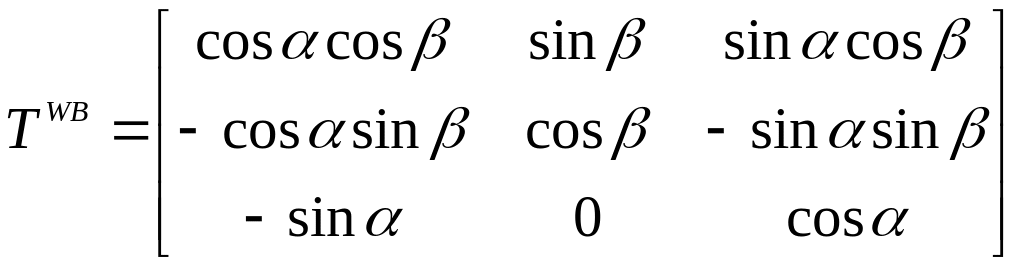
To transform back into body coordinates:

,

where

AERODYNAMIC ANGLES

The angle between the velocity vector and the plane of symmetry, measured in the plane x_w - y_w, is called sideslip angle and is denoted by the symbol β. Sideslip is positive when the relative wind is from right of the plane of symmetry, as shown in Figure 12.

Consider the projection of the velocity vector into the plane of symmetry, and assume some body-fixed coordinate system has been defined. The angle between this projection and x_b axis is called the angle-of-attack and is given the symbol α. It is positive when the relative wind is from below the x_b axis as shown in figure 13.

Figure 12 Sideslip angle, β. The axis y_b and velocity vector lie in the plane of the page

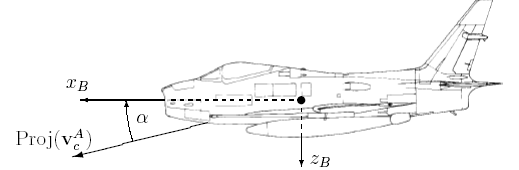
Figure 13 Angle-of Attack, α. Plane of the page is the aircraft plane of symmetry, x_b-z_b. Proj ( ) onto the plane of symmetry.