5.2. Знакопеременные ряды. Признак Лейбница

Числовой ряд называется знакопеременным рядом, если любые два соседних члена имеют противоположные знаки.

Отсюда следует, что существуют знакопеременные ряды двух типов. У знакопеременных рядов первого типа все члены, находящиеся на нечетных местах x₁, x₃, x₅,…положительны, а все члены, находящиеся на четных местах x₂, x₄, x₆,… – отрицательны.

У знакопеременных рядов второго типа наоборот: все члены, находящиеся на нечетных местах отрицательны, а на четных – положительны.

Если все члены знакопеременного ряда второго типа умножить на –1, то он превратиться в знакопеременный ряд первого типа, а потому достаточно рассмотреть только ряды первого типа.

Будем обозначать абсолютные величины членов знакопеременного ряда через . Следовательно, знакопеременный ряд первого типа можно записать следующим образом .

Достаточное условие сходимости знакопеременного ряда содержится в приводимой ниже теореме.

Теорема (признак) Лейбница. Если в знакопеременном ряде

(6.93)

абсолютные величины его членов, монотонно убывая,

стремятся к нулю, то такой ряд сходится, и его сумма S удовлетворяет неравенству 0 < S < p₁.

Доказательство. Сначала рассмотрим последовательность четных усеченных сумм ряда (6.93) и докажем, что члены этой последовательности возрастают, а сама последовательность ограничена. В самом деле, усеченную сумму можно представить следующим образом

. (6.94)

Изобразим числа на числовой оси (рис.69). Они изобразятся в виде точек, расположенных справа налево. В (6.94) все разности в скобках положительны и они изображаются в виде длин, не налегающих друг на друга n сегментов, отмеченных на рис.69 прямоугольниками.

Рис. 69

Сумма длин этих n сегментов равна , положительна и меньше длины сегмента [0, p₁], т.е. . Кроме того, с увеличением n на единицу, имеем, что , так как в этом случае, на рис.69 добавится еще один сегмент [p_2n+1, p_2n+2].

Итак, доказано, что последовательность возрастает и ограничена, а потому она имеет предел, который обозначим : .

Кроме того, имеем

_. (6.95)

Далее рассмотрим последовательность нечетных усеченных сумм ряда (6.93)

(6.96)

и докажем, что она также ограничена, но ее члены убывают.

Представим в следующем виде

(6.97)

и опять изобразим числа в виде точек на числовой оси, расположенных на ней справа налево (рис.70).

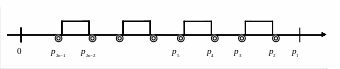
Рис. 70

Все разности в круглых скобках в правой части (6.97) положительны и они отмечены на рис.70 в виде не налегающих друг на друга (n – 1) сегментов – прямоугольников. Для получения S_2n-1, согласно (6.97), нужно из длины сегмента [0, p₁] вычесть длины сегментов [p₃, p₂],…,[p_2n-1, p_2n-2]. Отсюда следует справедливость неравенств 0 < S _2n-1 < p₁, а также, что последовательность (6.96) убывает, так как с увеличением n на единицу, на рис.70 слева добавляется еще один вычитаемый сегмент [p_2n+1, p_2n].

Итак, последовательность (6.96) убывает и ограничена, а потому она имеет предел. Из равенства S_2n= S_2n-1 – p_2n находим

.

Но последовательность (6.96) убывающая, поэтому получаем

(6.97)

Теперь для обеих последовательностей и из (6.95) и (6.97) следует, что 0 < S < p_1.

Наконец из того, что возрастающая последовательность и убывающая имеют один и тот же предел S, следует, что последовательность усеченных сумм ряда (6.93) также имеет число S своим пределом и стремится к S с двух сторон, причем четные усеченные суммы стремятся к S возрастая (слева), а нечетные убывая (справа). Таким образом, ряд (6.93) сходится и имеет сумму, равную S. Теорема доказана.

Следствие. При сохранении условий теоремы Лейбница:

1. абсолютная величина ошибки r_n= S – S_n приближенного равенства

не превышает абсолютной величины первого отброшенного члена (–1)ⁿ p_n+1, т.е.

(6.98)

и 2) знак ошибки r_n совпадает со знаком первого отброшенного члена

знак r_n= (–1)ⁿ. (6.99)

Действительно из равенства

получаем, что

(6.100)

Но ряд внутри квадратных скобок в правой части удовлетворяет условиям теоремы Лейбница, а потому его сумма положительна и меньше чем p_n+1. Отсюда следует (6.98). Кроме того, из (6.100) следует справедливость и (6.99).

Пример. Рассмотрим ряд

_(6.101)

Этот ряд называется полугармоническим, так как ряд, составленный из абсолютных значений членов этого ряда, является гармоническим рядом. Для исследуемого ряда выполнены все условия признака Лейбница, а потому он сходится, но поскольку ряд, состоящий из абсолютных значений членов этого ряда (т.е. гармонический ряд) расходится, поэтому, ряд (6.101) является неабсолютно (условно) сходящимся. Далее можно показать, что сумма ряда (6.101) равна ln2

.