5

3. Движение тела в неинерциальных системах отсчета

3.1. Силы инерции

Законы Ньютона справедливы лишь в инерциальных системах отсчета. При этом ускорение тела во всех инерциальных системах отсчета одинаково. Если некоторая система отсчета движется относительно инерциальной системы с ускорением (рис.3.1.), то такая система является неинерциальной. В этом случае ускорение тела в неинерциальной системе отсчета будет отличаться от ускорения в инерциальной системе. Ускорение в инерциальной системе в этом случае равно векторной сумме ускорений тела в неинерциальной системе и ускорения самой неинерциальной системы отсчета:

. (3.1)

Тогда сила, действующая на тело, равна . При тело будет двигаться по отношению к неинерциальной системе отсчета с ускорением – , т.е. так, как если бы на него действовала сила . Эту силу назовем силой инерции. Тогда по второму закону Ньютона получаем:

.

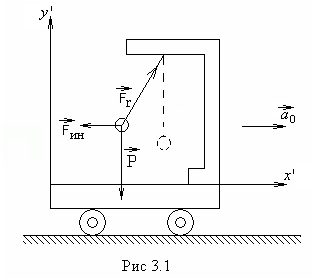Введение сил инерции дает возможность описывать движение тел в любых (как инерциальных, так и неинерциальных) системах отсчета с помощью одних и тех же уравнений движения. Следует иметь в виду, что силы инерции обусловлены не взаимодействием тел, а свойствами системы отсчета, по отношению к которой рассматривается движение. В этом смысле их можно назвать фиктивными силами.

Введение в рассмотрение сил инерции не является принципиально необходимым. Любое движение всегда можно рассматривать по отношению к инерциальной системе отсчета. Однако использование сил инерции дает возможность решить соответствующую задачу непосредственно по отношению к неинерциальной системе отсчета, что в ряде случаев оказывается существенно проще рассмотрения данного движения в инерциальной системе отсчета.

Характерным свойством сил инерции является их пропорциональность массе. Благодаря этому свойству силы инерции оказываются аналогичными силам тяготения.

Рассмотрим некоторые примеры движений в неинерциальных системах отсчета.

3.2. Равномерно вращающаяся система отсчета

3.2.1. Центробежная сила инерции

Рассмотрим диск, вращающийся относительно инерциальной системы отсчета с постоянной угловой скоростью . Свяжем с диском неинерциальную систему отсчета (рис.3.2). Рассмотрим точку M, покоящуюся относительно диска. Ее ускорение в неинерциальной системе отсчета . Ускорение точки M относительно инерциальной системы отсчета равно ускорению самого диска

г де  - угловая скорость диска, – радиус-вектор точки M. Эта формула определяет нормальное ускорение, направленное к центру диска (от точки M к точке O), т.е. противоположно радиус-вектору , поэтому перед выражением стоит знак минус.

Точку M можно удержать в покое относительно диска, например, с помощью растянутой пружины. При этом в пружине возникает сила упругости , уравновешиваемая силой инерции, т.е. . Тогда сила инерции равна и называется центробежной силой инерции.

3.2.2. Кориолисова сила инерции

При движении тела относительно неинерциальной вращающейся системы отсчета кроме центробежной силы инерции появляется еще сила Кориолиса.

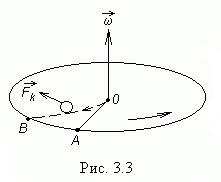Рассмотрим пример (рис.3.3).На горизонтально расположенном диске, который может вращаться вокруг вертикальной оси, проведем радиальную прямую ОА. В направлении этой прямой из точки О запустим шарик с постоянной скоростью . Если диск не вращается, шарик движется по ОА. Приведем диск во вращение с постоянной угловой скоростью . В этом случае траектория шарика ОВ будет отличаться от ОА. Следовательно, на шарик, движущийся с постоянной скоростью относительно вращающейся системы отсчета, действует сила, перпендикулярная к скорости . В результате действия этой силы скорость шарика меняет свое направление. Эту силу и называют силой Кориолиса.

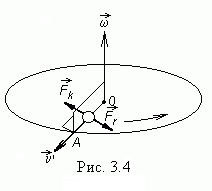Для того, чтобы заставить шарик катиться по радиальной прямой АВ равномерно вращающегося диска, его направляют по радиальному ребру (рис.3.4). В этом случае кориолисова сила уравновешивается силой реакции ребра , и скорость шарика остается постоянной.

Н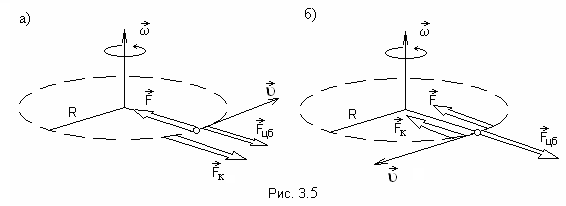 айдем выражение для силы Кориолиса. Пусть частица массой m движется относительно равномерно вращающегося диска по окружности с постоянной по величине скоростью . На рис.3.5.а) направления движения частицы и системы отсчета совпадают, на рис.3.5б) эти направления противоположны. Скорость частицы относительно неподвижной инерциальной системы отсчета для случая а) равна , где R – радиус вращения частицы. Для случая б) . Чтобы частица двигалась относительно инерциальной системы отсчета со скоростью , на нее должна действовать сила, направленная к центру окружности. Этой силой может быть, например, сила натяжения нити, которой частица привязана к оси вращения. Для случая а) имеем:

Здесь - сила, действующая на частицу в неинерциальной вращающейся системе отсчета; -центробежная сила инерции, вызванная вращением системы отсчета с угловой скоростью . Тогда есть сила Кориолиса, которая связана с движением самой частицы в неинерциальной системе отсчета.

Из последнего выражения видно, что сила Кориолиса совпадает по направлению с центробежной силой, т.е. направлена от центра диска.

Для случая б) получаем

.

Сила Кориолиса направлена к центру диска, т.е. противоположно центробежной силе инерции.

В векторной форме выражение для силы Кориолиса принимает вид:

.

Если точка покоится в неинерциальной системе отсчета, , поэтому действующая на нее сила Кориолиса равна нулю,

Ускорение частицы относительно инерциальной системы отсчета равно

где – радиус-вектор частицы. Ускорение называется переносным. Это ускорение, которым обладала бы частица, покоящаяся во вращающейся системе отсчета. Ускорение называется ускорением Кориолиса.