4. Преобразование координат

4.1. Представление вектора в однородной форме

В компьютерной графике приходиться манипулировать не только с точками, но и с векторами. В пространстве любой размерности точка и вектор описываются одинаковым числом параметров и в структуре хранения могут оказаться не различимыми. Действительно, такая запись

может означать как точку A, так и вектор A, как на рис. 4.1.

Представление в однородных координатах позволяет избавиться от такой неоднозначности. Принята договоренность считать:

– точка A; – вектор A.

Соглашение оказалось удачным, поскольку при этом:

- легко отличается точка от вектора;

- структура хранения данных единая как для точки, так и для вектора;

- соблюдаются все правила выполнения операций над векторами и точками.

Первые два утверждения очевидны. Проиллюстрируем последнее.

1) сумма двух векторов – вектор:

;

2) сумма точки и вектора – точка:

;

3) разность двух точек – вектор:

;

4) произведение скалярной величины на вектор – вектор:

;

5) линейная комбинация векторов – вектор:

; ;

(a, b – скалярные величины).

4.2. Преобразования координат в 2d, координатный фрейм

При изучении задачи преобразования модели использовали аффинные преобразования:

A₁ = M₀₁A₀.

При этом предполагалось – A₀ – точка A в начальном положении в некоторой СК, A₁ – та же точка в новом положении в той же СК.

Взглянем на эти преобразования по другому. Будем понимать: A₀ – точка A в исходной системе координат СК0 X₀Y₀, A₁ – та же точка A в новой СК1 X₁Y₁; M₀₁ – матрица преобразования точки A из СК0 в СК1.

Эта задача имеет другой геометрический смысл, отличный от ранее изученной, хотя при этом используются одни и те же преобразования. Чтобы отличить их, поменяем условные обозначения, вместо

будем использовать

,

когда речь идет о преобразованиях координат.

Таким образом это преобразование координат точки A из системы координат СК0 в СК1, где A₀ – точка A в СК0; A₁ – та же точка в СК1; F₀₁ – матрица аффинных преобразований в однородной форме.

Можно получить обратное соотношение ; естественно считать матрицей преобразования из СК1 в СК0 и обозначать F₁₀. Следовательно

, , .

Как и в случае преобразования модели, нам следует научиться целенаправленно назначать элементы матриц F₀₁ и F₁₀. Ни какая из них не имеет ни каких преимуществ перед другой, но, из соображений ясности понимания этого вопроса, удобнее изучать его с матрицей F₁₀.

Н а рис. 4.2 изображена исходная СК0 X₀Y₀ и новая СК1 X₁Y₁. СК1 задана относительно СК0: S – точка начала координат СК1; U – орт оси X₁; V – орт оси Y₁. Нам надо решить вопрос – если

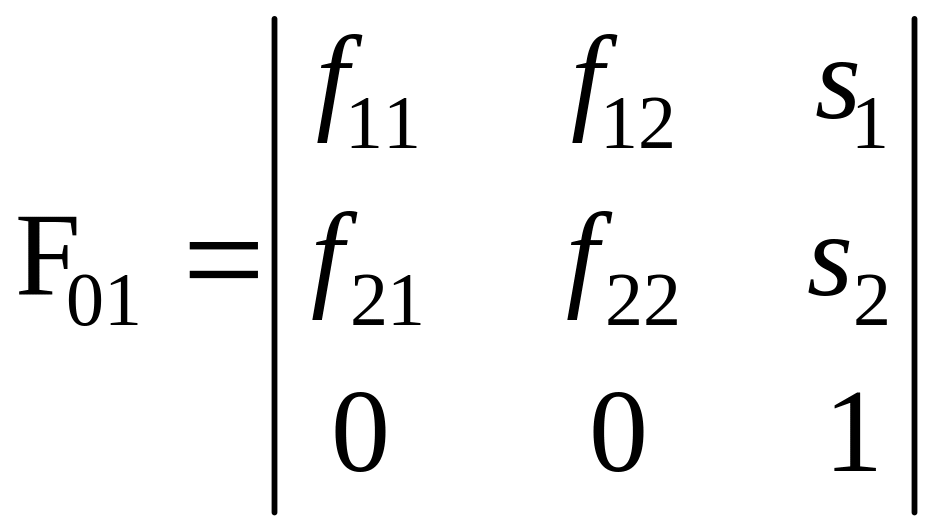
есть матрица преобразования из СК1 в СК0 и СК0 – исходная (начальная), то где находится начало СК1 относительно СК0 (где находится точка S в СК0), как направлены координатные оси X₁ и Y₁ относительно СК0 (каковы единичные вектора U и V относительно СК0).

Точка S в системе координат СК1 есть начало координат, представление ее в СК1 будет:

.

Поскольку F₁₀ – матрица преобразования координат из СК1 в СК0, то эта же точка в системе координат СК0 будет:

.

Следовательно, последний столбец в матрице F₁₀ задает положение начала координат СК1 относительно СК0.

Вектор U – орт оси X₁ СК1. Представление его в СК X₁Y₁ будет

.

Этот же вектор после преобразования в СК0

.

Следовательно, первый столбец в матрице F₁₀ задает единичный вектор оси X₁ относительно СК0.

Вектор V – орт оси Y₁ СК1. Представление его в СК X₁Y₁ будет

.

Этот же вектор после его преобразования в СК0

.

Следовательно, второй столбец в матрице F₁₀ задает единичный вектор оси Y₁ относительно СКО.

Общее правило. В матрице

,

• когда она понимается как координатный фрейм:

• первый столбец задает единичный вектор оси X₁ системы координат СК1 относительно СК0;

• второй столбец – единичный вектор оси Y₁ СК1 относительно СК0;

• третий столбец – точку положения начала СК1 относительно СК0.

В матрице

,

когда она понимается как координатный фрейм:

• первый столбец задает единичный вектор оси X₀ системы координат СК0 относительно СК1;

• второй столбец – единичный вектор оси Y₀ системы координат СК0 относительно СК1;

• третий столбец – точку положения начала СК0 относительно СК1.

Матрицы F₀₁ и F₁₀ – обратные, т.е. , и . Учитывая изложенное, рис. 4.2 можно уточнить, как это сделано на рис. 4.3.

М атрицы F₁₀ и F₀₁ определены как матрицы преобразования координат из СК1 в СК0 и из СК0 в СК1 соответственно. Но оказалось, что эти матрицы можно понимать и как матрицы, задающие систему координат СК1 относительно СК0 (F₁₀) или СК0 относительно СК1 (F₀₁). По этой причине, когда речь идет о преобразованиях координат, матрицу преобразования координат называют еще и координатным фреймом, вкладывая в это понятие другой смысл, как матрицы, задающей одну систему координат относительно другой. Понятие координатный фрейм в некоторых случаях существенно облегчает решение задач преобразования координат.

Например, в исходной СК0 задана новая СК1 (рис. 4.4).

Надо получить матрицу преобразования координат из СК1 в СК0, т.е. F₁₀. Как взяться за такую задачу? Вспомним, что F₁₀ одновременно является координатным фреймом, задающим привязку СК1 относительно СК0. При таком толковании F₁₀ ее третий столбец будет точка, задающая начало СК1: ; первый столбец будет представлением единичного вектора оси X₁ в СК0: ; второй столбец будет представлением единичного вектора оси Y₁ в СК0: . Собрав все вместе, получаем

,

т.е. матрицу преобразования координат из СК X₁Y₁ на рис. 4.4 в СК X₀Y₀.

Матрица преобразования F₀₁ может быть получена так: :

.

Еще несколько простых примеров.

; ; ; ; .