
2. Тензоры над трехмерным евклидовым пространством
2.1. Тензоры второго ранга
К понятию простейшего тензора — тензора второго ранга — мы подойдем конструктивно.
1. Для
этого рассмотрим векторные функции
(операторы)
![]() ,
действующие из
,
действующие из
![]() в
и линейные,
т.е.
в
и линейные,
т.е.
![]()
![]() и
и
![]() .
.
2. Простейшим
примером линейного оператора
![]() является всестороннее растяжение
пространства
является всестороннее растяжение
пространства
![]() (2.1.1)
(2.1.1)
и,
в частности, при
![]() ,
тождественное преобразование, другой
пример дает функция
,
тождественное преобразование, другой
пример дает функция
![]() . (2.1.2)
. (2.1.2)
В качестве еще одного примера рассмотрим обратимое линейное отображение вектора
![]()
на вектор
![]() (2.1.3)
(2.1.3)
с теми же компонентами в другом базисе.
3. Линейный оператор можно представить в виде
![]() . (2.1.4)
. (2.1.4)
Например,
оператор всестороннего растяжения
(2.1.1) с помощью соотношений Гиббса
![]() можно записать в виде
можно записать в виде
![]()
или (2.1.4) с
![]() .
.
При мы получаем тождественное преобразование, записываемое с помощью
![]() .
(2.1.5)
.
(2.1.5)
Отображение
(2.1.2) записывается с использованием
всегда выполнимого представления
вектора
![]() и тождества (1.31) как
и тождества (1.31) как
![]()
или в виде (2.1.4) с
![]() .
.
Обратимое
линейное отображение (2.1.3) с помощью
соотношений Гиббса
![]() можно записать в явном виде
можно записать в явном виде
![]() ,
,
представимом как (2.1.4) с
![]() .
.
4. Итак,
скалярное умножение вектора-аргумента
справа на символический объект
![]() однозначно задает произвольный линейный
оператор. С помощью представления
(2.1.4) легко показать, что множество
линейных операторов образует векторное
пространство. Действительно, линейные
операции с операторами, вводимые
правилами
однозначно задает произвольный линейный
оператор. С помощью представления
(2.1.4) легко показать, что множество
линейных операторов образует векторное
пространство. Действительно, линейные
операции с операторами, вводимые
правилами
![]() ,
,
![]() ,
замкнуты, поскольку
,
замкнуты, поскольку
![]() есть вектор
;
другие аксиомы векторного пространства
проверяются элементарно.
есть вектор
;
другие аксиомы векторного пространства
проверяются элементарно.
Линейное
пространство линейных операторов
обладает специфической структурой,
обусловленной наличием в нем еще одной
бинарной алгебраической операцией —
умножением, в качестве которого выступает
операция последовательного применения
линейных операторов,
определяемая
правилом
![]() .
Действительно,
.
Действительно,
![]()
![]() есть вектор
.
Тождественное преобразование
есть вектор
.
Тождественное преобразование
![]() является единицей в этом множестве и
мы можем написать
является единицей в этом множестве и
мы можем написать
![]() .
.
5. Обратимся
теперь к вопросу представления объекта
,
задающего линейный оператор. Из примеров
п.2 видно, что
устроен с помощью линейных операций
сложения и умножения на скаляр и некой
бинарной операции умножения векторов,
для упорядоченной их пары
![]() обозначаемой
обозначаемой
![]() и называемой диадным
умножением.
Диадное умножение линейно по обоим
своим аргументам:
и называемой диадным
умножением.
Диадное умножение линейно по обоим
своим аргументам:
![]() ,
,
![]() ,
что следует из
,
что следует из
![]() ,
,
![]() .
Диадное умножение некоммутативно, т.е.
.
Диадное умножение некоммутативно, т.е.
![]() ,
поскольку
,
поскольку
![]()
![]() .
Диадное умножение векторов называют
диадой,
а линейнную комбинацию диад — диадиком
или тензором
второго ранга.
Таким образом, линейный оператор в общем
случае представляется в виде диадика
(тензора второго ранга)
.
Диадное умножение векторов называют
диадой,
а линейнную комбинацию диад — диадиком
или тензором
второго ранга.
Таким образом, линейный оператор в общем
случае представляется в виде диадика
(тензора второго ранга)
![]() (2.1.6)
(2.1.6)
6. Любой тензор второго ранга можно представить в виде суммы трех диад. С использованием (2.1.5)
![]() , (2.1.7)
, (2.1.7)
где
![]() ,
,
![]() — произвольная некомпланарная тройка
векторов, а
— произвольная некомпланарная тройка
векторов, а
![]() — тройка сопряженных к ним векторов.
Представление (2.1.7) не зависит от выбора
исходной некомпланарной тройки векторов
(базиса), потому что представление
(2.1.5) от него не зависит.
— тройка сопряженных к ним векторов.
Представление (2.1.7) не зависит от выбора
исходной некомпланарной тройки векторов
(базиса), потому что представление
(2.1.5) от него не зависит.
Если
векторы
![]() линейно независимы, то трехчленное
представление (2.1.7) неприводимо.
линейно независимы, то трехчленное
представление (2.1.7) неприводимо.
В
случае компланарности векторов
сумма в (2.1.7) может быть приведена к
двучленной. Пусть, например,
![]() ,
тогда тензор принимает вид
,
тогда тензор принимает вид
![]() . (2.1.8)
. (2.1.8)
Дальнейшее
приведение возможно, если
![]() и
и
![]() коллинеарны, т.е.
коллинеарны, т.е.
![]() .
В этом случае тензор сводится к диаде
.
В этом случае тензор сводится к диаде
![]() . (2.1.9)
. (2.1.9)
В любом случае представление такое не единственно.
7. Легко
увидеть, что отображение (2.1.4) с трехчленным
неприводимым представлением тензора
(2.1.7) осуществляет отображение
![]() на все пространство
на все пространство
![]() (такое отображение называется обратимым,
а соответствующий тензор невырожденным),
данное отображение с двучленным
неприводимым представлением (2.1.8)
осуществляет отображение
на некоторое двумерное подпространство
(такое отображение называется обратимым,
а соответствующий тензор невырожденным),
данное отображение с двучленным
неприводимым представлением (2.1.8)
осуществляет отображение
на некоторое двумерное подпространство
![]() ,
а отображение с одночленным неприводимым
представлением (2.1.9) осуществляет
отображение
на некоторое одномерное подпространство
,
а отображение с одночленным неприводимым
представлением (2.1.9) осуществляет
отображение
на некоторое одномерное подпространство
![]() .
.
Если
для некоторых векторов
![]() будет
будет
![]() ,
то и для любой их линейной комбинации,
очевидно,
,
то и для любой их линейной комбинации,
очевидно,
![]() .
Поэтому подмножество
.
Поэтому подмножество
![]() ,
состоящее из всех прообразов нулевого
вектора
,
состоящее из всех прообразов нулевого
вектора
![]() ,
также является подпространством
пространства
,
также является подпространством
пространства
![]() и называется ядром
линейного
оператора (2.1.4). Очевидно
и называется ядром
линейного
оператора (2.1.4). Очевидно
![]() .
Число
.
Число
![]() называется рангом
линейного оператора, а
называется рангом
линейного оператора, а
![]() — его дефектом,
сумма дефекта
и ранга линейного отображения равна
трем. Равенство нулю дефекта T
равносильно
невырожденности этого тензора, если
дефект T
равен
единице, то этот тензор называют
однократно вырожденным, если двум —
двукратно вырожденным. Наконец, если
дефект T
равен
трем,
т.е.
— его дефектом,
сумма дефекта
и ранга линейного отображения равна
трем. Равенство нулю дефекта T
равносильно
невырожденности этого тензора, если
дефект T
равен
единице, то этот тензор называют
однократно вырожденным, если двум —
двукратно вырожденным. Наконец, если
дефект T
равен
трем,
т.е.
![]() ,
то T = 0.
,
то T = 0.
Для
обратимого линейного отображения,
осуществляемого невырожденным тензором
T,
существует обратное линейное отображение,
осуществляемое обратным тензором
![]() .
Легко показать (рекомендуется это
сделать), что такой тензор однозначно
связан с исходным тензором соотношением
.
Легко показать (рекомендуется это
сделать), что такой тензор однозначно
связан с исходным тензором соотношением
![]() . (2.1.10)
. (2.1.10)
Покажите наиболее простым способом, что диада есть двухкратно вырожденный, а симметризованная диада — однократно вырожденный тензор.
8. Если
разложить каждый из векторов
![]() в представлении тензора (2.1.6) по базису
в представлении тензора (2.1.6) по базису
![]() ,
,
![]() и использовать линейность диадного
умножения, тензор записывается в виде
и использовать линейность диадного
умножения, тензор записывается в виде
![]() ,
,
![]() (2.1.12)
(2.1.12)
— разложения
по системе девяти диад
![]() .
Нетрудно показать их линейную независимость
(рекомендуется сделать), поэтому
пространство тензоров девятимерно.
Числа
.
Нетрудно показать их линейную независимость
(рекомендуется сделать), поэтому
пространство тензоров девятимерно.
Числа
![]() называются дважды
контравариантными компонентами тензора
.
Эти компоненты образуют матрицу:
называются дважды
контравариантными компонентами тензора
.
Эти компоненты образуют матрицу:
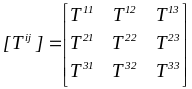 .
.
Разлагая
каждый из векторов
в (2.1.6) по базису
![]() ,
мы получим разложение
,
мы получим разложение
![]() с помощью дважды
ковариантных компонент тензора
,
а выбирая для разложения пары
сопряженные базисы,
с помощью дважды
ковариантных компонент тензора
,
а выбирая для разложения пары
сопряженные базисы,
![]() ,
— смешанные
компоненты
тензора
.
Четыре матрицы
,
,
— смешанные
компоненты
тензора
.
Четыре матрицы
,
![]() ,
,
![]() ,
,
![]() компонент разложения тензора
по базисам
,
компонент разложения тензора
по базисам
,
![]() ,
,
![]() ,
,
![]() ,
конечно, не равны.
,
конечно, не равны.
9. Из
формул преобразования основного или
взаимного базисов следует закон
преобразования диадного базиса. Например,
для базиса
![]() из (1.2.2), (1.3.11) с учетом билинейности
диадного произведения следует
из (1.2.2), (1.3.11) с учетом билинейности
диадного произведения следует
![]() . (2.1.13)
. (2.1.13)
Поскольку T с равным правом разлагается по старому и новому базисам,
![]() ,
(2.1.14)
,
(2.1.14)
из
последнего равенства и (2.1.13) с использованием
линейной независимости диад
![]() получаем
получаем
![]() .
.
Отсюда становится понятной структура формул преобразования компонент произвольных разложений тензора второго ранга:
 (2.1.15)
(2.1.15)
10. Понятие тензора второго ранга оказывается более общим, чем понятие линейного оператора. Можно сказать, что линейный оператор есть одна из “профессий” тензора, с помощью которой мы к нему конструктивно подошли. Другой “профессией” тензора является билинейная форма, когда он выступает в качестве линейной по каждому из двух векторных аргументов скалярозначной функции:
![]() . (2.1.11)
. (2.1.11)
Основные
факты об алгебраической структуре
множества тензоров второго ранга и их
представлениях, установленные нами
выше с использованием частной “профессии”
тензора как линейного оператора,
универсальны. Сказанное в п.7, однако,
не справедливо по отношению к отображению
(2.1.13), структура прообразов нуля у
которого иная. 12. Резюме. Итак, диадное
умножение есть билинейное отображение
пары векторов из трехмерного векторного
пространства в вектор некоторого
![]() -мерного
векторного пространства, называемого
тензорным пространством. Тензорное
пространство является натянутым на
диады;
кроме них в нем содержатся их всевозможные
линейные комбинации, которые и называются
тензорами (второго ранга). Тензор второго
ранга в общем случае не сводится к диаде,
а сводится к линейной комбинации трех
диад. Пространство тензоров есть
векторное пространство, обладающее
специфической структурой.
-мерного
векторного пространства, называемого
тензорным пространством. Тензорное
пространство является натянутым на
диады;
кроме них в нем содержатся их всевозможные
линейные комбинации, которые и называются
тензорами (второго ранга). Тензор второго
ранга в общем случае не сводится к диаде,
а сводится к линейной комбинации трех
диад. Пространство тензоров есть
векторное пространство, обладающее
специфической структурой.
