2.3. Взаимное расположение двух прямых на плоскости

Две прямые на плоскости или совпадают, или параллельны, или пересекаются. Если направляющие векторы прямых a₁x+b₁y+c₁=0 и a₂x+b₂y+c₂=0 коллинеарны (то есть если ), то прямые либо совпадают, либо параллельны. В первом случае , во втором случае . Если же направляющие векторы не коллинеарны ( ), то прямые пересекаются. Итак, получаем:

прямые совпадают тогда и только тогда, когда

;

прямые параллельны тогда и только тогда, когда ;

прямые пересекаются тогда и только тогда, когда

.

Если прямые параллельны или совпадают, то угол между прямыми считается равным нулю. Если прямые пересекаются, то угол между ними считается равным меньшему из четырех образованных ими углов. Таким образом, угол между прямыми может быть либо прямым, либо острым, то есть косинус этого угла равен модулю косинуса угла между направляющими векторами. Поскольку направляющие векторы прямых a₁x+b₁y+c₁=0 и a₂x+b₂y+c₂=0 имеют координаты (b₁, –a₁) и (b₂, –a₂) соответственно, то косинус угла между прямыми вычисляется по формуле:

cos = .

Из этой формулы получаем условие перпендикулярности двух прямых на плоскости: прямые a₁x+b₁y+c₁=0 и a₂x+b₂y+c₂=0 перпендикулярны тогда и только тогда, когда

a₁a₂+b₁b₂=0.

2.4. Расстояние от точки до прямой на плоскости

Если точка М_о(х_о;у_о) принадлежит прямой l, то расстояние (М_о; l) от точки до прямой считается равным нулю. Если точка М_о(х_о;у_о) не принадлежит прямой l, то расстояние (М_о; l) от точки до прямой равно длине перпендикуляра М_оМ, опущенного из точки М_о на прямую l. Если прямая l задана уравнением ax+by+c=0, то ее нормальный вектор =(a; b) является направляющим вектором перпендикулярной прямой М_оМ. Поэтому параметрическое уравнение прямой М_оМ имеет вид: 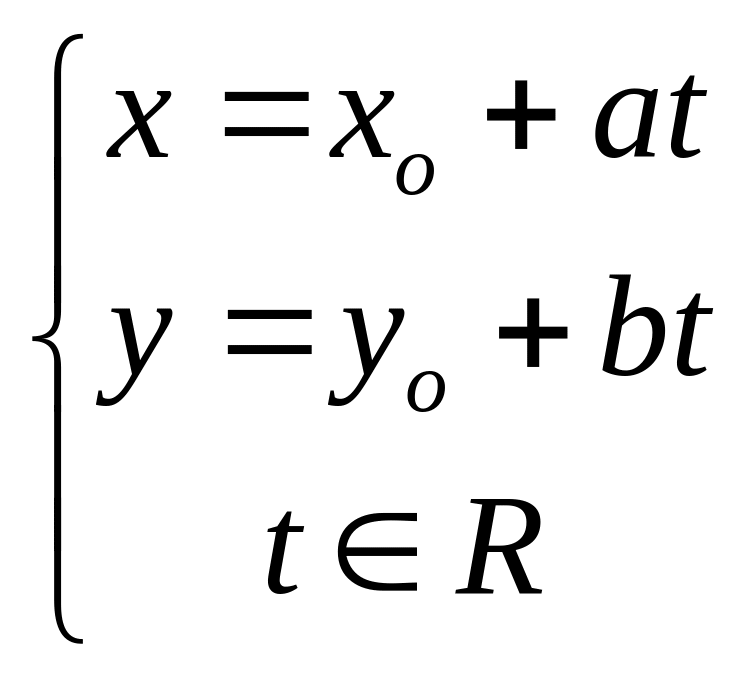. Пусть М(х;у). Подставим выражения для х и у в уравнение прямой l: a(x_о+аt)+b(y_о+bt)+c=0. Отсюда t = . С другой стороны, М_оМ = = . Подставив в это выражение найденное выражение для t, получим: М_оМ = = . Окончательно получаем формулу расстояния от точки до прямой:

(М_о; l) = .

Замечание. Эта формула справедлива и для точки, лежащей на прямой: в этом случае дробь равна нулю, как и расстояние от точки до прямой.

2.5. Эллипс, гипербола, парабола

1^о. Эллипсом называют множество таких точек М плоскости, что сумма расстояний от М до двух фиксированных точек плоскости постоянна. Указанные две точки называются фокусами эллипса.

Пусть фокусы эллипса – точки F₁ и F₂, F₁F₂ = 2c, и пусть для точек М эллипса сумма МF₁+МF₂ = 2а. Тогда а>c. Выберем систему координат так, чтобы фокусы имели координаты F₁(–с;0), F₂(с;0). Тогда точка М(х;у) принадлежит эллипсу тогда и только тогда, когда

.

Возведя обе части этого равенства в квадрат, получим:

Отсюда после преобразований имеем:

,

. Еще раз возводя в квадрат, получаем:

,

,

.

Так как а > c, то а²–с² > 0, поэтому можно обозначить b² = а²–с², где b > 0. Тогда получаем: . Если, наконец, разделить обе части уравнения на а²b², то получим каноническое уравнение эллипса с расположением фокусов на оси абсцисс:

, a>b.

Из уравнения видно, что –axa, –byb, то есть эллипс расположен внутри прямоугольника, задаваемого этими неравенствами. Точки (–a;0), (a;0), (0;–b), (0;b) называются вершинами эллипса, число а – большой полуосью эллипса, число b – малой полуосью. Из уравнения также видно, что вместе с любой точкой (х,у) эллипсу принадлежат точки (х,–у), (–х,у) и (–х,–у). Отсюда следует, что эллипс имеет две оси симметрии (оси координат) и центр симметрии (начало координат). Число  = называется эксцентриситетом эллипса. Так как а > c > 0, то  < 1.

Замечание. Если выбрать систему координат так, что F₁(0;–с), F₂(0;с), МF₁+МF₂ = 2b, то получится то же каноническое уравнение , но в этом случае a<b.

2^о. Гиперболой называют множество таких точек М плоскости, что модуль разности расстояний от М до двух фиксированных точек плоскости постоянен. Указанные две точки называются фокусами гиперболы.

Пусть фокусы гиперболы – точки F₁ и F₂, F₁F₂ = 2c, и пусть для точек М гиперболы модуль МF₁–МF₂= 2а. Тогда а<c. Выберем систему координат так, чтобы фокусы имели координаты F₁(–с;0), F₂(с;0). Тогда точка М(х;у) принадлежит гиперболе тогда и только тогда, когда

.

Выполним преобразования так же, как в предыдущем пункте, и обозначим b² = с²–а², где b > 0. Тогда получаем: . Если, наконец, разделить обе части уравнения на а²b², то получим каноническое уравнение гиперболы с расположением фокусов на оси абсцисс:

.

Из уравнения видно, что xa, поэтому гипербола расположена вне полосы, задаваемой этим неравенством, то есть состоит из двух ветвей. Точки (–a;0), (a;0) называются вершинами гиперболы, число а – действительной полуосью гиперболы, число b – мнимой полуосью. Из уравнения также видно, что вместе с любой точкой (х,у) гиперболе принадлежат точки (х,–у), (–х,у) и (–х,–у). Отсюда следует, что гипербола имеет две оси симметрии (оси координат) и центр симметрии (начало координат). Число  = называется эксцентриситетом гиперболы. Так как c > a > 0, то  > 1.

В отличие от эллипса, гипербола является неограниченной линией. Из уравнения видно, что при х, стремящемся к бесконечности, модуль отношения стремится к числу . Это означает, что прямые являются асимптотами гиперболы: при х, стремящемся к бесконечности, точки гиперболы неограниченно приближаются к этим прямым.

Замечание. Если выбрать систему координат так, что F₁(0;–с), F₂(0;с), МF₁–МF₂ = 2b, то получится каноническое уравнение . Эта гипербола имеет те же асимптоты, а ее вершины имеют координаты (0;–b) и (0;b). Гиперболы и называются сопряженными гиперболами.

3^о. Параболой называют множество таких точек М плоскости, что расстояния от М до точки F и до прямой d, лежащих в этой плоскости, одинаковы. Точка F называется фокусом, а прямая d – директрисой параболы.

Пусть (F;d) = p. Выберем систему координат так, чтобы фокус имел координаты F( ;0), а директриса имела уравнение x+ =0. Тогда точка М(х;у) принадлежит параболе тогда и только тогда, когда MF = (М;d). Используя формулу расстояния от точки до прямой, получаем:

.

Возведя обе части этого равенства в квадрат, получим:

, – откуда получаем каноническое уравнение параболы:

у² = 2рх.

Из уравнения видно, что x  0, то есть парабола расположена в правой полуплоскости. Точка (0;0) называется вершиной параболы. Из уравнения также видно, что вместе с любой точкой (х,у) параболе принадлежит точка (х,–у). Отсюда следует, что парабола имеет ось симметрии – ось абсцисс. Парабола является неограниченной линией, и если х+, то у.

Замечание. Если выбрать систему координат так, что F(– ;0), а директриса имеет уравнение x– =0, то получится каноническое уравнение у² = –2рх; парабола лежит в левой полуплоскости. Если выбрать систему координат так, что F(0; ), а директриса имеет уравнение у+ =0, то получится каноническое уравнение х² = 2ру; парабола лежит в верхней полуплоскости. Если выбрать систему координат так, что F(0;– ), а директриса имеет уравнение у– =0, то получится каноническое уравнение х² = –2ру; парабола лежит в нижней полуплоскости.

Как видно, каждая из линий имеет каноническое уравнение только в некоторой специальной системе координат. Можно сказать, что линия является эллипсом (или гиперболой, или параболой), если существует такая система координат, в которой линия задается уравнением соответствующего вида.

Пример. Рассмотрим график квадратичной функции: y = ax²+bx+c, a0. Перепишем формулу в виде: , . Перенесем начало координат в точку , тогда новые координаты точки связаны со старыми формулами: 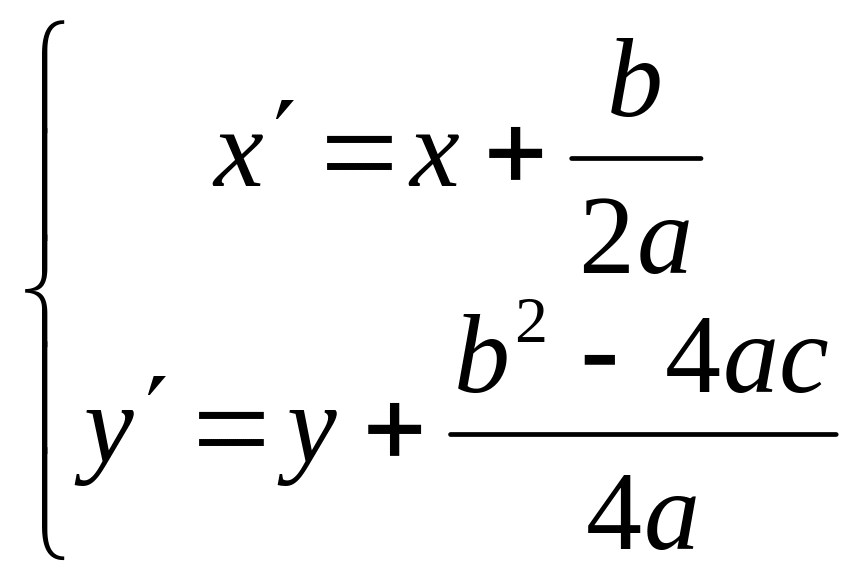. В новой системе координат уравнение линии имеет вид: . Если а>0, то, обозначив через 2р, получим уравнение – каноническое уравнение параболы (в верхней полуплоскости). Аналогично при а<0 получим уравнение – каноническое уравнение параболы (в нижней полуплоскости).

Итак, график квадратичной функции является параболой. 