
Новосибирский Государственный Университет, 3 курс экономического факультета
Эконометрия-I
ПОВТОРЕНИЯ
Матричная алгебра Определения
 называется
вектором-столбцом размерности
называется
вектором-столбцом размерности
![]() .
.
![]() называется
вектором-строкой размерности
.
называется
вектором-строкой размерности
.
 называется матрицей
размерности
называется матрицей
размерности
![]() .
.
Сумма
матриц
![]() и
и
![]() (
):
(
):
![]() ,
,
![]() (
)
(
)
Произведение
матриц
(
)
и
(![]() ):
):
![]() ,
(
,
(![]() )
)
Скалярное
произведение векторов-столбцов
![]() (
(![]() )
и
)
и
![]() (
):
(
):
![]() .
.
Квадратичная
форма вектора-столбца
![]() (
)и
матрицы
(
(
)и
матрицы
(![]() ):
):
![]() .
.
Произведение
матрицы
(
)
на
скаляр
![]() :
:
![]() ,
(
)
,
(
)
Транспонирование
матрицы
(
):![]() ,
(
,
(![]() )
)
След
матрицы
(
):![]() .
.
Рангом
(![]() )
матрицы
называется количество линейно независимых
столбцов (равное количеству линейно
независимых строк). Матрица
(
)
имеет полный ранг по столбцам, если
)
матрицы
называется количество линейно независимых
столбцов (равное количеству линейно
независимых строк). Матрица
(
)
имеет полный ранг по столбцам, если
![]() .
Матрица
(
)
имеет полный ранг по строкам, если
.
Матрица
(
)
имеет полный ранг по строкам, если
![]() .
.
Матрица ( ) называется невырожденной (неособенной), если . В противном случае она называется вырожденной.
Матрица
(
)
называется диагональной, если
![]() при
при
![]() .
Для диагональной матрицы используется
обозначение
.
Для диагональной матрицы используется
обозначение
![]() .
.
Матрица
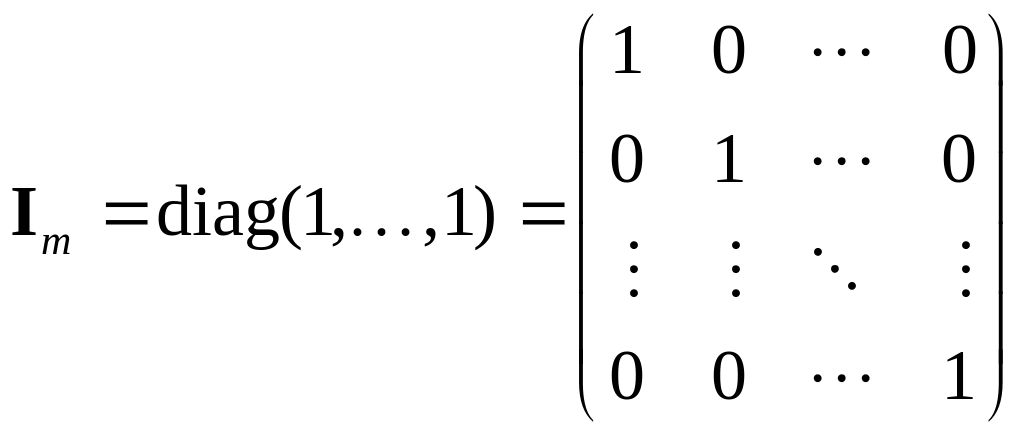 (
)
называется единичной.
(
)
называется единичной.
Матрица
(
)
называется симметричной (симметрической),
если![]() .
.
Матрица
(
)
называется верхней треугольной, если
при
![]() .
Матрица
(
)
называется нижней треугольной, если
при
.
Матрица
(
)
называется нижней треугольной, если
при
![]() .
.
Матрица
![]() (
)
называется обратной матрицей к матрице
(
),
если
(
)
называется обратной матрицей к матрице
(
),
если
![]() .
.
Матрица
(
)
называется идемпотентной, если![]() .
.
Векторы-столбцы
(
)
и
(
)
называются ортогональными, если их
скалярное произведение равно нулю:
![]() .
.
Матрица
(
),
где
![]() ,
называется ортогональной, если ее
столбцы ортогональны, т.е.
,
называется ортогональной, если ее
столбцы ортогональны, т.е.![]() .
.
Матрица
(
)
называется положительно определенной,
если для любого вектора-столбца
![]() (
)
выполняется
(
)
выполняется
![]() .
Матрица
(
)
называется отрицатльно определенной,
если для любого вектора-столбца
(
)
выполняется
.
Матрица
(
)
называется отрицатльно определенной,
если для любого вектора-столбца
(
)
выполняется
![]() .
.
Матрица
(
)
называется положительно полуопределенной
(неотрицательно определенной), если для
любого вектора-столбца
(
)
выполняется
![]() .
Матрица
(
)
называется отрицательно полуопределенной
(неположительно определенной), если для
любого вектора-столбца
(
)
выполняется
.
Матрица
(
)
называется отрицательно полуопределенной
(неположительно определенной), если для
любого вектора-столбца
(
)
выполняется
![]() .
.
Определителем
матрицы
(
)называется
![]() ,
где
,
где
![]() — номер любой строки, а матрицы
— номер любой строки, а матрицы
![]() (
(![]() )
получены из матрицы
путем вычеркивания
-й
строки и
)
получены из матрицы
путем вычеркивания
-й
строки и
![]() -го
столбца.
-го
столбца.
Для
матрицы
(
)
уравнение
![]() называется характеристическим уравнением.
Решение этого уравнения,
называется характеристическим уравнением.
Решение этого уравнения,
![]() называется собственным числом (собственным
значением) матрицы
.
Вектор
называется собственным числом (собственным
значением) матрицы
.
Вектор
![]() (
)
называется собственным вектором матрицы
,
соответствующим собственному числу
,
если
(
)
называется собственным вектором матрицы
,
соответствующим собственному числу
,
если
![]() .
.
Прямое
произведение (произведение Кронекера)
матриц
(
)
и
(![]() ):
):
 ,
(
,
(![]() ).
).
Свойства матриц
Сложение матриц
![]() (коммутативность).
(коммутативность).
![]() (ассоциативность).
(ассоциативность).
Произведение матриц
В
общем случае
![]() (свойство коммутативности не выполнено).
(свойство коммутативности не выполнено).
![]() (ассоциативность).
(ассоциативность).
![]() и
и
![]() (дистрибутивность).
(дистрибутивность).
![]() для матрицы
(
).
для матрицы
(
).
![]() .
.
Ранг
Для
матрицы
(
)
выполнено
![]() .
.
![]()
Если
матрица
(
)
является невырожденной, то для матрицы
(
)
выполнено
![]() .
Если матрица
(
.
Если матрица
(![]() )
является невырожденной, то для матрицы
(
)
выполнено
)
является невырожденной, то для матрицы
(
)
выполнено
![]() .
.
![]() .
.
Cлед
![]() .
.
![]() .
.
![]() .
.
![]() .
.
![]() .
.
![]() .
.
![]() .
.
![]() ,
где матрица
(
)
имеет полный ранг по столбцам, т.е.
.
,
где матрица
(
)
имеет полный ранг по столбцам, т.е.
.
![]() ,
где
и
,
где
и
![]() — квадратные матрицы.
— квадратные матрицы.
Транспонирование
![]() .
.
![]() .
.
Определитель
Для
матрицы
(![]() )
)
![]() .
.
![]() .
.
![]() .
.
![]() для матрицы
(
).
для матрицы
(
).
![]() .
.
![]() .
.
Если
матрица
(
)
является треугольной (например,
диагональной), то
![]() .
.
![]() .
.
![]() .
.
![]() для матрицы
(
)
и векторов-столбцов
для матрицы
(
)
и векторов-столбцов
![]() (
).
(
).
![]() ,
где
и
— квадратные матрицы.
,
где
и
— квадратные матрицы.
![]() ,
где
и
— квадратные невырожденные матрицы.
,
где
и
— квадратные невырожденные матрицы.
Матрица
(
)
является невырожденной (
)
тогда и только тогда, когда
![]() .
.
Обращение
Если обратная матрица существует, то она единственна (в частности, левая и правая обратная матрица совпадают).
Матрица ( ) имеет обратную ( ) тогда и только тогда, когда она является невырожденной ( ).
Матрица ( ) имеет обратную ( ) тогда и только тогда, когда .
Обозначим
через
![]() элементы
обратной матрицы
.
Тогда
элементы
обратной матрицы
.
Тогда
![]() ,
где
,
где
![]() (
)
получены из матрицы
путем вычеркивания
-й
строки и
-го
столбца.
(
)
получены из матрицы
путем вычеркивания
-й
строки и
-го
столбца.
Во всех приводимых ниже формулах предполагается, что существуют обратные матрицы там, где это требуется.
Для
матрицы
(![]() )
)
 .
.
![]() .
.
![]() .
.
![]() .
.
![]() .
.
Если
(
)
— ортогональная матрица, то
![]() .
.
Для
диагональной матрицы
выполнено
![]() .
.
![]() .
.
![]() .
.
![]() .
.
 ,
где
и
— квадратные матрицы.
,
где
и
— квадратные матрицы.
 ,
где
и
— квадратные матрицы.
,
где
и
— квадратные матрицы.
Положительно определенные матрицы
Если
матрица
положительно
определенная, то
![]() .
Если матрица
положительно
полуопределенная, то
.
Если матрица
положительно
полуопределенная, то
![]() .
.
Если
матрица
положительно (полу-)определенная, то
матрица
![]() отрицательно (полу-)определенная.
отрицательно (полу-)определенная.
Если матрица положительно определенная, то обратная матрица также положительно определенная.
Если
матрицы
и
положительно (полу-)определенные, то
матрицы
![]() и
и
![]() также положительно (полу-)определенные.
также положительно (полу-)определенные.
Если
матрица
положительно определенная, а
положительно полуопределенная, то
![]() .
Если
положительно определенная, то
.
Если
положительно определенная, то
![]() .
.
Матрицы
![]() и
и
![]() (
)
являются симметричными положительно
полуопределенными для любых матриц
(
)
и
(
)
являются симметричными положительно
полуопределенными для любых матриц
(
)
и
![]() (
).
(
).
Если
матрица
(
)
имеет полный ранг по столбцам, то матрица
(
)
симметричная положительно определенная.
Если матрица
(
)
положительно определенная, а матрица
![]() (
)
имеет полный ранг по столбцам, то матрица
(
)
симметричная положительно определенная.
(
)
имеет полный ранг по столбцам, то матрица
(
)
симметричная положительно определенная.
Если
матрица
(
)
положительно полуопределенная, то
существует верхняя треугольная матрица
![]() (
),
такая что
(
),
такая что
![]() .
Также существует нижняя треугольная
матрица
.
Также существует нижняя треугольная
матрица
![]() (
),
такая что
(
),
такая что
![]() .
Такое представление матрицы называется
разложением Холецкого (триангуляризацией).
.
Такое представление матрицы называется
разложением Холецкого (триангуляризацией).
Идемпотентные матрицы
Если
матрица
идемпотентная, то матрица
![]() тоже идемпотентная, причем
тоже идемпотентная, причем
![]() .
.
Если
матрица
симметричная и идемпотентная, то
![]() .
.
Матрицы
![]() и
и
![]() являются
симметричными и идемпотентными для
любой матрицы
(
),
имеющей полный ранг по столбцам. При
этом
являются
симметричными и идемпотентными для
любой матрицы
(
),
имеющей полный ранг по столбцам. При
этом
![]() и
и
![]() .
.
Собственные числа и векторы
Для
матрицы
(
)
![]() является многочленом
является многочленом
![]() -й
степени (характеристическим многочленом)
и имеет
корней,
-й
степени (характеристическим многочленом)
и имеет
корней,
![]() (среди которых могут быть кратные). По
определению
являются собственными числами матрицы
.
(среди которых могут быть кратные). По
определению
являются собственными числами матрицы
.
У матрицы ( ) существует не больше различных собственных чисел.
Если
— собственный вектор матрицы
,
соответствующий собственному числу
,
то для любого скаляра
![]()
![]() тоже собственный вектор, соответствующий
собственному числу
.
тоже собственный вектор, соответствующий
собственному числу
.
Если
— собственные числа матрицы
,
то
![]() .
.
Если
— собственные числа матрицы
,
то
![]() .
.
Если матрица идемпотентная, то все ее собственные числа равны 0 или 1.
Все собственные числа вещественной симметричной матрицы вещественны.
Если
![]() и
и
![]() — собственные векторы вещественной
симметричной матрицы, соответствующие
двум различным собственным числам, то
они ортогональны:
— собственные векторы вещественной
симметричной матрицы, соответствующие
двум различным собственным числам, то
они ортогональны:
![]() .
.
Если
матрица
(
)
является вещественной и симметричной,
то существуют матрицы
![]() и
и
![]() ,
где
(
)
— ортогональная матрица (
,
где
(
)
— ортогональная матрица (![]() ),
столбцы которой — собственные векторы
матрицы
,
а
(
)
— диагональная матрица, состоящая из
соответствующих собственных чисел
матрицы
,
такие что выполнено
),
столбцы которой — собственные векторы
матрицы
,
а
(
)
— диагональная матрица, состоящая из
соответствующих собственных чисел
матрицы
,
такие что выполнено
![]() .
.
Если
матрица
(
)
является вещественной, симметричной,
невырожднной, то
![]() .
.
Вещественная симметричная матрица является положительно полуопределенной (определенной), тогда и только тогда, когда все ее собственные числа неотрицательны (положительны). Вещественная симметричная матрица является отрицательно полуопределенной (определенной), тогда и только тогда, когда все ее собственные числа неположительны (отрицательны).
Если
матрица
(
)
является вещественной, симметричной и
положительно полуопределенной, то
![]() ,
где
,
где
![]() (
)
— вещественная, симметричная и
положительно полуопределенная матрица.
(
)
— вещественная, симметричная и
положительно полуопределенная матрица.
Пусть
![]() —
собственные числа вещественной
симметричной матрицы
(
).
Тогда собственый вектор
—
собственные числа вещественной
симметричной матрицы
(
).
Тогда собственый вектор
![]() ,
соответствующий наибольшему собственому
числу
,
соответствующий наибольшему собственому
числу
![]() ,
является решением решением задачи
,
является решением решением задачи
![]()
Пусть
—
собственные числа вещественной
симметричной матрицы
(
).
Тогда
![]() и
и
![]() .
.
Произведение Кронекера
![]() и
и
![]() .
.
![]() .
.
![]() .
.
![]() .
.
![]() .
.
![]() .
.
![]() для матриц
(
)
и
для матриц
(
)
и
![]() (
).
(
).
![]() .
.
![]()
