1.2 Одномерное преобразование Фурье

 

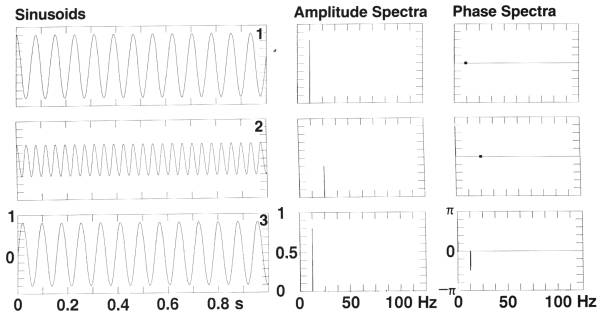
Рассмотрим следующий эксперимент. Зафиксируем один конец пружины, а к другому концу подвесим груз. Отведем груз вниз на определенную величину, например, на 0.8 единиц расстояния и отпустим его. Предположим, что пружина является упругой, т.е. она колеблется до бесконечности. В начале движения зададим время равное нулю. Смещение веса в функции времени должно изменяться от амплитуды +0.8 до –0.8. Если имеется устройство, которое может отслеживать амплитуду смещения в функции времени, оно запишет синусоидальную кривую (см. рис. 1-1, изображение 1). Измерим время между двумя последовательными пиками; вы увидите, что оно равно 0.080с (80мс). Этот временной интервал называется периодом пружины и зависит от константы, которая представляет собой меру жесткости пружины. Мы говорим, что пружина выполнила один цикл движения за один период времени. Сосчитаем количество циклов в одной секунде; должно получиться 12.5 циклов. Это называется частотой, ассоциированной с движением пружины. Один цикл в секунду (cps) – один герц (Гц). Единицу делим на 0.080с и получаем 12.5Гц, т.е. частота – это величина, обратная периоду.

Повторим этот эксперимент, используя более жесткую пружину. Зададим второй пружине максимальное смещение 0.4 единицы. Движение пружины отслеживается в виде другой синусоиды (рис. 1-1, изображение 2). Период и частота пружины – соответственно 0.040с и 25Гц. Чтобы зафиксировать результаты измерений, построим график амплитуды перемещения каждой пружины в функции частоты; получим амплитудный спектр (рис. 1-1, средняя колонка).

Работа с двумя идентичными пружинами, отпустим пружину 1 при максимальном смещении 0.8 единиц и в начале движения зададим время, равное нулю. Когда пружина 1 проходит через положение, соответствующее нулевой амплитуде, приводим в движение вторую пружину при таком же максимальном смещении (0.8). Движение пружины 1 показано на изображении 1, а движение пружины 2 – на изображении 3 рисунка 1-1. Поскольку пружины начали движение при одном и том же смещении, амплитудные спектры обеих синусоидальных функций будут одинаковыми. Однако, между временными функциями на изображениях 1 и 3 можно видеть различие. В частности, когда синусоида на изображении 1 принимает значение, соответствующее максимальной амплитуде, амплитуда синусоиды на изображении 3 равно нулю. Пружина 2 была приведена в движение с задержкой на 20мс, эквивалентной одной четверти полного цикла. Эта задержка представляет собой разность двух синусоид, показанных на изображении 1 и 3. Полный цикл эквивалентен 360° или 2p. Следовательно, временная задержка в одну четверть цикла эквивалентна отставанию по фазе на +90°.

Рис.1-1 При отслеживании движения пружины во времени получается синусоидальная кривая. Максимальная амплитуда представляет максимальное смещение груза от положения, соответствующего нерастянутой пружины. Положительная амплитуда соответствует движению пружины вверх. Время между двумя последовательными пиками – период синусоиды, обратная величина периода – частота. Временная задержка начала движения одной пружины относительно начала движения другой пружины определяется как отставание по фазе. Фазовые спектры (спектры отставания по фазе со знаком минус) различают синусоиды 1 и 3.

 

Фаза определяется как отставание по фазе со знаком минус (Robinson и Treitel, 1980). Таким образом, отрицательное временное смещение соответствует положительной величине фазы. Если на рис.1-1 мы применим временное смещение, равное одной четверти полного цикла (т.е. 20 мс) к синусоиде на изображении 3 в отрицательном направлении во времени, мы получим синусоиду, представленную на изображении 1. Хотя их амплитудные спектры идентичны, синусоиды можно различить по их фазовым спектрам (рис.1-1, правая колонка).

Эксперимент закончен. Что мы узнали? Во-первых, движение пружины можно описать синусоидальной функцией. Во-вторых (и это более важно), синусоидальное движение полностью описывается частотой, амплитудой и фазой. Этот опыт показывает, как описывать движение пружины как функцию времени и частоты.

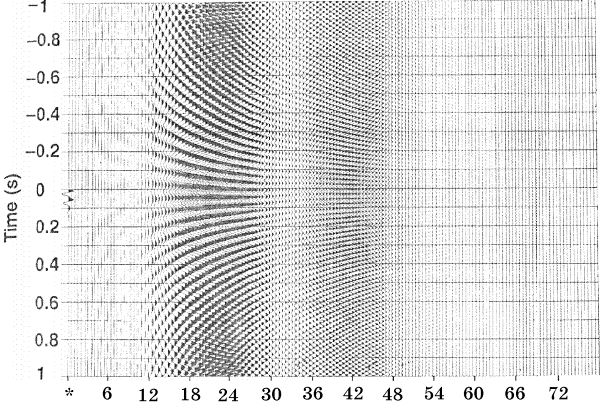
Сейчас представим, что имеется группа пружин, каждая из которых совершает синусоидальное движение с определенной частотой, амплитудой и фазой. Синусоидальная характеристика всех движений показана на рис.1-2. Выполним положение движения всех пружин, сложив все трассы; получим зависимость от времени сигнала, обозначенный звездочкой рис.1-2 (первая трасса). Положение (или синтез) позволяет нам преобразовать движение из частотной области во временную. Это преобразование является обратным, т.е. сигнал во временной области может быть разбит (или разложен) на синусоидальные составляющие в частотной области.

Математически этот двусторонний процесс выполняется с помощью преобразования Фурье. На практике стандартным алгоритмом, используемым на цифровых компьютерах, является быстрое преобразование Фурье (БПФ; FFT – Fast Fourier Transformation). Анализ зависящего от времени сигнала на частотные составляющие выполняется посредством прямого преобразования Фурье, а синтез частотных составляющих в сигнал во временной области выполняется путем обратного преобразования Фурье.

На рис.1-3 представлено преобразование Фурье зависящего от времени сигнала на рис.1-2. Амплитудный и фазовый спектры образуют более уплотненное представление в частотной области синусоид на рис.1-2. Можно видеть параллельность между двумя типами изображений. В частности, амплитудный спектр содержит большой и относительно малый пик около 20 и 40Гц соответственно. Более темные полосы соответствуют большим амплитудам на рис1-2 при одних и тех же частотах. С другой стороны, зоны слабых амплитуд около 30Гц и на низко- и высокочастотных концах спектра также заметны в обоих типах представлений. Следует помнить, что кривая амплитудного спектра представляет амплитуды отдельных синусоидальных компонент в функции частоты.

Исследуем фазовый спектр. Из опыта с пружиной вспомним, что отставание во времени какой-либо частотной составляющей было также выражено как задержка по фазе. Чтобы улучшить задержку по фазе трассы как функцию частоты, рисунка 1-2 (см. рис.1-4). Будем следовать максимумам, которые пересекаются нулевой маркой времени. Отметим, что максимумы расположены выше нулевой марки времени (т.е. имеют отрицательные значения времени) на низкочастотном конце спектра. Затем они переходят на положительную сторону временной оси около частоты 20Гц и остаются на этой стороне на протяжении оставшейся части оси частот. Путь, который они проходят на рис.1-4, можно построить в виде фазового спектра рисунка 1-3. Если все максимумы выровнять вдоль нулевой марки времени на рис.1-4, соответствующий сигнал во временной области будет иметь нуль-фазовый спектр. В этом случае все синусоиды будут усиливать друг друга, что обусловит появление максимальной величины при нулевом времени (рис.1-11).

Рис.1-2 Можно выполнить наложение группы синусоидальных движений с различными частотами, амплитудами и задержками по фазе с целью синтезирования зависимой от времени формы волны (см. трассу, обозначенную звездочкой).

 

Физическое значение амплитудного спектра понять проще, чем физическое значение фазового спектра. Оба эти спектра будут рассмотрены в данной главе далее. Основные математические подробности преобразования Фурье даны в Приложении А.