40. Полный дифференциал.

Полный дифференциал, функции f (x, у, z,...) нескольких независимых переменных — выражение , в случае, когда оно отличается от полного приращения Df = f (x + Dx, y + Dy, z + Dz,…) - f (x, y, z, …) на величину, бесконечно малую по сравнению с

41.Производные сложных функций.

Т е о р е м а  1. Если функция   имеет производную в точке  , а функция   имеет производную в точке  , то сложная функция                                                      (1)

имеет производную (по  ) в точке   и справедливо равенство

                                                      (2)

или

.                                                             (3)

Д о к а з а т е л ь с т в о. Зададим  , ему соответствует значение  . Придадим   приращение  , это вызовет приращение  . Так как функция   имеет производную в точке  , то на основании равенства (2) § 4.1, имеем

,                                               (4)

где   при  .

Будем считать, что  . Равенство (4) при этом соглашении выполняется, т. к. если подставить в него  , то получится  .

Разделим теперь равенство (4) на  :

.                                               (5)

Пусть    стремится к нулю. Тогда  , потому что функция   имеет производную в точке   и, следовательно, непрерывна.

Переходим в равенство (5) к пределу при  . Тогда   и  , поэтому получим

.

Теорема доказана.

Формула (1) может быть усложнена. Например, если  ,  ,   и все три функции имеют производные в соответствующих точках, то  .

П р и м е р  1.     .

Полагаем  ,  ,  . Тогда

.

П р и м е р  2.   .

Полагаем  . Тогда

.

Обычно при вычислениях вспомогательные переменные   не вводят, а только подразумевают их.

В случае примера 1 вычисления выглядят так:

.

Или еще короче

.

42. Производная по направлению. Градиент

Теорема. Пусть функция f (x, y) определена вместе со своими частными производными f'_x, f'_у, f''_xy, f''_yx в некоторой окрестности точки (x₀,y₀), причем производные f''_xy и f''_yx непрерывны в этой точке, тогда f''_xy (x₀,y₀) = f''_yx (x₀,y₀).

Согласно этой теореме смешанные производные можно вычислять в любом порядке и нет необходимости находить обе смешанные производные.

Пусть дана функция u = f (x, y, z), определенная в некоторой области пространства Oxyz.

Определение. Вектор с координатами  ,  ,   называется градиентом функции u = f (x, y, z) в точке M(x, y, z) и обозначается grad u = + + .

Под производной функции u = f (x, y, z) в данном направлении   понимается выражение   =  cosa +  cosb +  cosg, где cosa, cosb, cosg – направляющие косинусы вектора   (рис. 43).

 

 

 

Рис. 43

 

Производная   представляет собой скорость изменения функции в данном направлении.

Теорема. Производная функции по направлению равна проекции градиента этой функции на данное направление (в соответствующей точке).

Как известно, проекция вектора на другой вектор имеет максимальное значение, если оба вектора совпадают по направлению.

Градиент функции в данной точке указывает напрвление наиболее быстрого возрастания функции.

Величина градиента, т.е. | grad u | =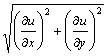  обозначается tg j и определяет крутизну наибольшего ската или подъема поверхности u = f (x, y).

Пример 24. Найти производную функции z = x²+y²–xy+2x+3y в точке M(–9,–1) в направлении, идущем от этой точки к точке N(4,5).

Решение. Вычислим z'_x и z'_y.

z'_x = 2x–y+2, z'_y = 2y–x+3. Найдем значения этих производных в точке M.

z'_x|_M = –18+1+2=–15, z'_y|_M = –2+9+3=10.

Найдем вектор  :  = (4+9, 5+1)=(13,6). Так как этот вектор лежит в плоскости, то его направление определяется углом между этим вектором и осью Ox, а производная по направлению определяется по формуле   =  cosa +  sina.

Вычислим cosa и sina: cosa = = ,

sina = .

Пример 25. Найти градиент функции u=  в точке M(6,2,3).

Решение. Вычислим градиент функции по формуле

 grad u = + + .

= ;  = ;  = .

Тогда grad u = + + .

Подставляя в это соотношение x = 6, y = 2, z = 3, получим grad u= + + .