49Билет Свободные колебания систем с одной степенью свободы. Колебания без затухания

В данном случае и в дальнейшем ограничимся рассмотрением таких колебаний, для которых справедлив закон Гука и принцип независимости действия сил.Рассмотрим простейшую систему, состоящую из груза, подвешенного на вертикально расположенной пружине (рис. 12.6). Влиянием собственного веса пружин пренебрегаем. Направим ось x вдоль оси пружины вниз.За начало отсчета 0 возьмем положение статического равновесия груза Q.

В этом положении пружина растянута на величину  = Q/C, где С  жесткость пружины. Рассмотрим движение груза в произвольный момент времени t. Отклонение центра массы груза в этот момент от положения статического равновесия вниз обозначим через х. Получаем: ; ; .

При составлении уравнения движения будем исходить из принципа Даламбера, который заключается в том, что к движущейся с ускорением системе применимы соотношения статики при условии, что в число внешних сил включена фиктивная сила инерции, равная произведению массы на ускорение и направленная против ускорения. Полагаем, что скорость dx/dt и ускорение d²x/dt² совпадают по направлению с отклонением X. При отклонении груза возникает упругая сила Р_упр которая стремится вернуть груз в состояние равновесия и потому называется восстанавливающей силой.

Дифференциальное уравнение колебаний получим, спроектировав все действующие силы на вертикальную ось: . Отсюда имеем: ,или ,где .

Решением уравнения (12.3) будет: . (12.5)

где А и В  постоянные интегрирования, зависящие от начальных условий, т.е. от положения груза m = Q / g и его скорости dx/dt в момент времени t = 0.

Если заданы начальная координата груза х₀ и начальная скорость ₀, то из (12.5) определим: ; .

Полагая и , решение (12.5) можно представить в виде: . Или , где   амплитуда колебаний, определяемая формулой: .

Величина ₀t +  называется фазой колебаний, а величина   сдвигом фазы. На основании (12.7)  может быть определена из условия tg = х₀₀/₀.

Уравнение (12.7) выражает процесс чисто периодического собственного колебания системы. График его представлен на рис. 12.7.

Период колебаний Т определяется из условия, что при увеличении времени t на величину Т аргумент, стоящий под знаком синуса, изменится на 2: .

Период представляет собой время, в течение которого совершается одно колебание. Если Т  время одного колебания, то в 2 секунд будет происходить ₀ колебаний. Поэтому величина ₀ и носит название круговой частоты (в отличие от секундной частоты f = 1/Т): . Круговую частоту часто называют частотой собственных колебаний системы, поскольку она, как это видно из (12.4), зависит не от начальных обстоятельств колебательного процесса, а от величины олеблющейся массы и жесткости системы. Формуле (12.4) можно придать вид: , (12.8)

где g  ускорение свободного падения, м/с²; _с  статическое удлинение пружины под действием груза Q.

Билет50

Логарифмический декремент затухания

Натуральный логарифм отношения следующих друг за другом через период амплитуд характеризует темп колебаний и называется логарифмическим декрементом затухания , равным: .

При не слишком быстром процессе затухания, когда уменьшение амплитуды  за цикл значительно меньше самой амплитуды , можно записать: , , (если разложить в ряд и ограничиться, ввиду малости последующих членов, двумя его первыми членами). Тогда: ,

Сравнивая (12.9) и (12.10), имеем: , т.е. логарифмический декремент равен отношению уменьшения амплитуды за один цикл к значению амплитуды этого цикла.

В момент времени, когда перемещение системы достигает максимума, ее полная энергия равна потенциальной энергии: .

Потеря энергии за один цикл составит: .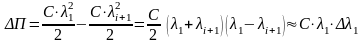

Относительное рассеяние энергии:

называют коэффициентом поглощения. Сравнивая (12.11) и (12.12), видим, что коэффициент поглощения вдвое больше логарифмического декремента. Другими словами, логарифмический декремент равен половине рассеяния энергии за один цикл колебаний.

Измеряя в нескольких местах записи амплитуды затухающих колебаний ₁, _i+1 или потерю энергии за цикл по формулам (12.11) и (12.12), можно найти логарифмический декремент и, следовательно, коэффициент затухания .