Распределение Максвелла-Больцмана
Распределение молекул газа по координатам и скоростям при наличии произвольного потенциального поля описывается распределением Максвелла-Больцмана:
,
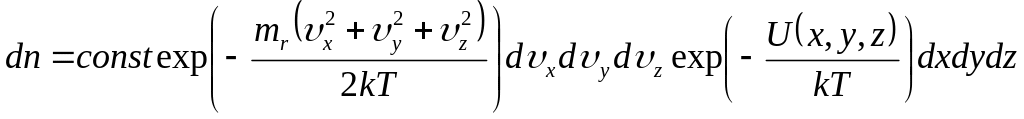где
– число молекул, находящихся в шестимерном
пространстве в элементе объема
,
– потенциальная энергия молекулы во
внешнем силовом поле в точке с координатами
x,
y,
z
и проекциями скорости
.Распределение
Максвелла-Больцмана представляет собой
произведение двух функций распределения:
одна из них описывает распределения по
координатам, а другая – по скоростям.
Броуновское движение. Флуктуации и их проявления.
Одним из наиболее убедительных доказательств движения молекул служит явление броуновского движения, открытое в 1827 г. английским ботаником Броуном при изучении взвешенных в воде мельчайших спор. Скорость движения броуновских частиц возрастает с повышением температуры и уменьшением размеров частиц. Эти закономерности можно объяснить, если принять, что движения частиц возникают вследствие ударов, испытываемых ими со стороны движущихся молекул жидкости или газа, в которых они находятся.
При полной беспорядочности молекулярных движений казалось бы толчки молекул должны компенсировать друг друга и частицы должны оставаться неподвижными. Однако это означает, что лишь среднее число ударов разных направлений одинаково. Отклонение от средних значений тех или иных величин, которые происходят в малом объеме или в течение малых промежутков времени, называются флуктуациями. Такие отклонения имеют место для малых частиц, для которых число толчков сравнительно невелико, так что преобладание числа ударов то одного, то другого направления становится заметным.
Количественная теория броуновского движения впервые дана Эйнштейном и независимо от него Смолуховским (1905 г.).
Предположим для простоты, что частица
имеет форму сферы радиуса «а».
Сила трения, согласно формуле Стокса,
где
– коэффициент внутреннего трения,
– скорость движения частицы. Уравнение
движения частицы при этом имеет вид:
,
где
– равнодействующая сил, вызванных
ударами молекул. В проекции на ось OX:
.
Нам требуется найти среднее значение
квадрата проекции смещения:
Преобразуем предыдущее уравнение,
умножив его на x:
.
Используем тождества:
;
.
После подстановки:
.
Усредним
полученное уравнение:
.
Поскольку движение хаотично:
,
,
,
.
Поскольку броуновская частица находится
в состоянии термодинамического
равновесия, то:
.
Следовательно:
.
Поэтому:
.
Перепишем данное уравнение, введя
обозначение
:
.
В результате интегрирования полученного
уравнения:
.
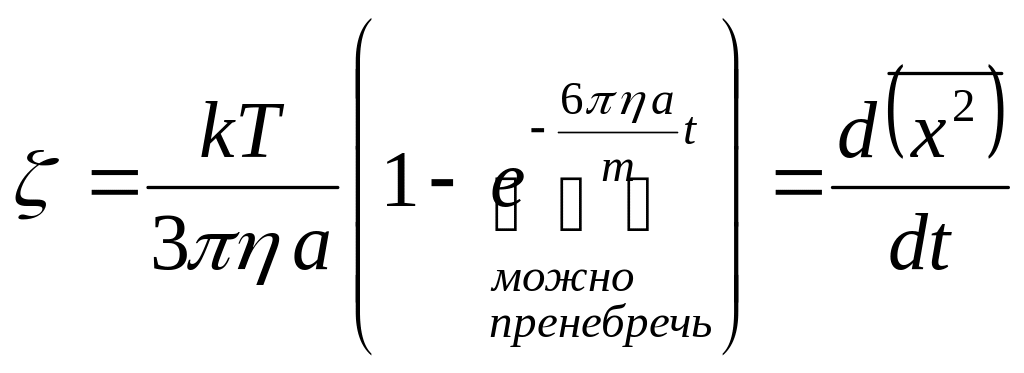Для конечных промежутков времени
:
.
Принимая во внимание, что
получаем:
– формула Эйнштейна:
среднее значение квадрата смещения
броуновской частицы пропорционально
этому промежутку времени.
Энтропия и вероятность состояния системы
Неравенство
выражает второе начало термодинамики
в изолированной системе. Согласно этому
закону необратимые процессы в изолированной
системе приводят к росту ее энтропии
до некоторого максимального значения,
которое соответствует достижению
системой равновесного состояния.
Переход системы от неравновесного состояния к равновесному всегда является переходом от менее вероятных состояний к более вероятным (например: расширение газа, смешение двух газов). Больцман в 1896 г. предложил, что между энтропией и термодинамической вероятностью W должна быть прямая зависимость:
S ~ lnW.
Макс Планк в 1906 г. нашел, что коэффициентом
пропорциональности является постоянная
Больцмана
:
.
Статистический смысл второго начала термодинамики: всякий процесс в природе протекает в сторону увеличения вероятности состояния системы. Второе начало не столь абсолютно, как первое начало термодинамики.