1.4. Формулы

Пусть - множество булевых функций. Формулой надFназывается выражениелибо переменная, либо формула надF.

Fназывается базисом формулы,f– главной (внешней) операцией,t_i– подформулами.

Всякой формуле однозначно соответствует некоторая функцияf. Это соответствие задается алгоритмом интерпретации, который позволяет вычислить значение функции при заданных значениях переменных.

Зная таблицы истинности для функций базиса можно вычислить таблицу той функции, которую реализует данная формула.

Примеры.

1.

x1	x2	x1 x2
0	0	0	0	0	0
0	1	0	0	1	1
1	0	0	1	0	1
1	1	1	1	1	1

Функция реализует дизъюнкцию на базисе.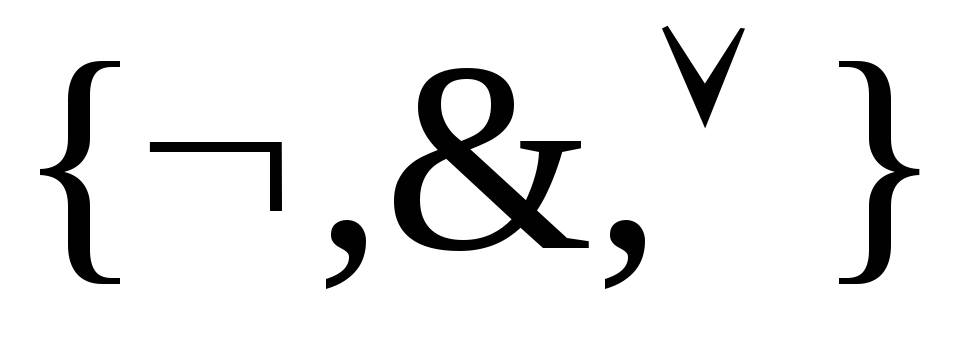

2.

x1	x2	x1~ x2
0	0	1	0	0
0	1	0	1	1
1	0	0	0	1
1	1	1	0	0

Функция реализует дизъюнкцию на базисе.

Таким образом каждая формула определяет некоторую логическую функцию, которую можно представить в виде таблицы истинности для этой формулы. Если в формуле имеется nпеременных, то возможны 2ⁿразличных истинностных значений для этой формулы. Следовательно, таблица истинности будет иметь 2ⁿстрок.

1.5. Равносильные формулы

Одна функция может иметь множество реализаций над данным базисом (т. е. ее можно записать с помощью различных формул). Формулы, реализующие одну и ту же функцию, называют равносильными. Обозначают .

Пример.

Пусть ,.

Доказать, что.

Равносильность двух формул можно доказать с помощью таблиц истинности. Формулы равносильны, если их значения истинности совпадают на любом наборе значений истинности, входящих в них переменных.

Таблица истинности для формулы А.

x	y	z	x~y	xz	A
0	0	0	1	0	0
0	0	1	1	0	0
0	1	0	0	0	1
0	1	1	0	0	1
1	0	0	0	0	1
1	0	1	0	1	1
1	1	0	1	0	0
1	1	1	1	1	1

Таблица истинности для формулы B.

x	y	z			xz	B
0	0	0	0	0	0	0
0	0	1	0	0	0	0
0	1	0	0	1	0	1
0	1	1	0	1	0	1
1	0	0	1	0	0	1
1	0	1	1	0	1	1
1	1	0	0	0	0	0
1	1	1	0	0	1	1

Тот факт, что равносильность формул логики высказываний можно проверить непосредственно, связан с тем, что переменные, входящие в формулу могут принимать конечное число значений (2ⁿ).

Но, если в формуле большое количество переменных, то вычисление всех значений истинности для формулы становится очень трудоемкой задачей.

Равносильность формул логики высказываний аналогична тождествам элементарной алгебры, известным из средней школы. Но тождественное равенство алгебраических формул нельзя проверить простым перебором значений, т. к. число возможных значений переменных неограниченно, следовательно, доказательство равносильности никогда не закончится. В элементарной алгебре тождественные равенства формул устанавливаются с помощью небольшого числа основных тождеств – законов, связывающих между собой арифметические операции.

Для логики имеют место следующие равносильности(рассмотрим только формулы, которые содержат знаки):

1. Коммутативный

А ВВ А АВ=ВА

2. Ассоциативный

А(В С)(А В)  С А(ВС)=(АВ)С

3. Дистрибутивный

А(ВС)(А В)(А С) А(В С)=АВ АС

4. Идемпотентности

А АА А·АА

5. Поглощения

А АВА А(А В)А

6. А 0А А·0 = 0

7. А 1=1 А·1=А

8. А =1 А =0

9. Закон де Моргана

10. = 0= 1

11 Двойное отрицание

= А

12. АВ В

13 А~В=А·В

14 АВ= ·В А·

15. А В = А В = А·В

16. А В ==
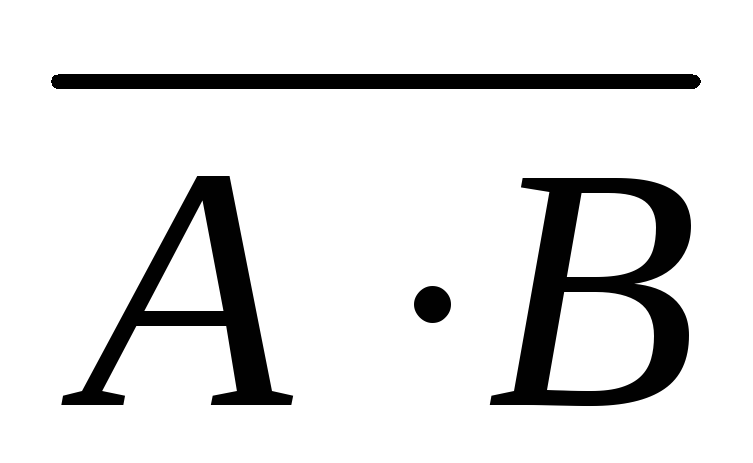