1. Задача о брахистохроне
Постановка задачи. В вертикальной плоскости заданы 2 точки на различных уровнях. Требуется соединить их некоторой гладкой линией (без изломов), скатываясь по которой, тяжёлый материальный шарик под воздействием лишь силы тяжести (трение не учитывается) пройдёт путь из верхней точки в нижнюю за кратчайшее время.
Воспользуемся
законом сохранения энергии в
:
в любой точке кривой сумма потенциальной
и кинетической энергии шарика постоянна.
Будем считать, что в точке 0 сумма равна
0, получаем
,
где
– масса шарика;
– ускорение свободного падения;
– его скорость.
.
С другой стороны
;
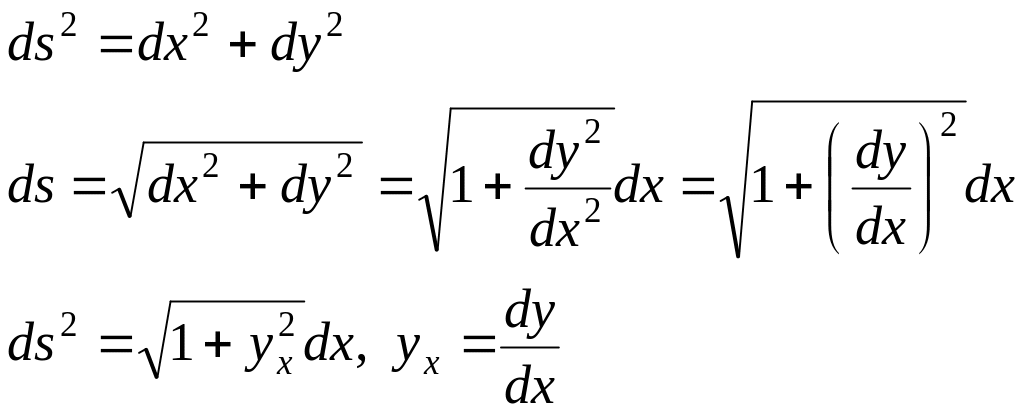
Тогда
.
Проинтегрируем обе части этого равенства:
– время скатывания
по кривой
.
Введём множество функций:
.
Тогда задача о брахистохроне примет
вид:
.
Эта задача была одной из первых задач, которая была поставлена и решена с помощью метода вариаций. Отсюда и название вариационное исчисление.
2. Основная задача. Обобщение. О численном решении.
Основной задачей вариационного исчисления является обобщение задачи о брахистохроне.
– время скатывания по кривой . Введём множество функций: . Тогда задача о брахистохроне примет вид: .
О.
непрерывная вместе со своей первой
производной и удовлетворяющая условию
называется допустимой
кривой.
Обозначим
через
– множество всех допустимых кривых
(рис. 1). Каждой допустимой кривой
поставим в соответствие функционал
,
где функция
.
Основная задача вариационного исчисления
имеет вид:
(1)
Допустимая
кривая
называется минималью,
если
.
Минималь – это аналог оптимального
плана.
О.
называется слабой
минималью
и обозначают СМ, если
для некоторого
.
Здесь
-окрестность
в пространстве
кривой
,
то есть
.
Слабая минималь – это аналог локального оптимального плана.
3.Вариации допустимых кривых и функционала
Пусть
дана некоторая допустимая кривая
,
тогда функция
называется вариацией
этой допустимой кривой,
если
снова является допустимой, то есть
.
Удобно
вариацию представлять в виде:
,
где
– описывает форму вариации, а множитель
её величину. Аналог в конечномерном
программировании:
.
Ясно,
что при
,
поэтому функцию
также называют вариацией
допустимой кривой.
Из
определения допустимых кривых вытекает,
что некоторая функция
будет вариацией тогда и только тогда,
когда
1)
;
2)
.
Обозначим
через
.
Для нашей задачи ясно, что некоторая
вариация
подходит сразу для всех допустимых
кривых.
Вариация
называется тривиальной,
так как она оставляет любую допустимую
кривую на месте. Вариация – основной
инструмент исследования основной задачи
вариационного исчисления.
О. Зафиксируем некоторую допустимую кривую и вариацию , тогда если допустимо разложение
,
то коэффициент при
называется первой
вариацией функционала,
а коэффициент при
– второй
вариацией функционала.
Получим для основной задачи вариационного исчисления вид 1-ой и 2-ой вариации. Из теории разложения функции в ряд вытекает, что 1-ой вариации функционала вид:
(2)
Из
соотношения (2) видно, что если зафиксировано
,
то первая вариация представляет из себя
некоторое число. Из теории разложения
функции в ряд следует, что 2-ая вариация
функционала имеет вид:
Видно,
что 2-ая вариация представляет из себя
некоторое число при фиксированных
.