Образец выполнения контрольной работы № 4 дифференциальное исчисление функции одной переменной

 

 

 

задача № 1

  Требуется исследовать функции

а)               б)               в)

 

методами дифференциального исчисления и построить их графики по плану.

1. Найти область определения функции.

2. Выяснить, является ли функция четной или нечетной, т.е. симметричен ли ее график относительно оси ординат или начала координат.

3. Найти вертикальные и невертикальные асимптоты графика функции.

4. Найти интервалы монотонности, т.е. интервалы возрастания и убывания функции, точки экстремума.

5. Найти интервалы выпуклости и вогнутости функции, точки перегиба.

6. Построить график функции, используя все собранные данные (если их окажется недостаточно, чтобы представить график функции, то найти несколько дополнительных точек, например, точки пересечения с осями координат).

 

Решение

а) Воспользуемся схемой полного исследования (см. 4.10).

1. областью определения функции y = x⁴ – 2x² + 1 является вся числовая прямая, т.е. (см. 4.2) х  (-∞, ∞).

2. Проверим, является ли функция четной или нечетной.

Найдем

f(-х) = (-x)⁴ – 2(-x)² + 1 = x⁴ – 2x² + 1 = f(х).

 

т.к. f(-х) = f(х) (см. 4.4), то функция является четной. ее график симметричен относительно оси ординат.

3. Найдем асимптоты.

а) Т.к. х = (-∞; ∞), то вертикальных асимптот нет.

 

б) Наклонную асимптоту ищем в виде у = kх + b, где (см. 4.6.3).

 

 

 

= (по правилу Лопиталя) =

 

 

наклонной асимптоты нет.

4. Найдем интервалы монотонности и точки экстремума функции (см. 4.7 и см. 4.8)

 

у^/ = (x⁴ – 2x² + 1)^/ = 4x³ – 4x.

 

 

Найдем критические точки I-го рода, для чего приравняем первую производную к нулю (см. 4.7)

 

у^/ = 0    4x³ – 4x = 0    4х(x² – 1) = 0    x₁ = 0,  x² – 1 = 0

 

 

точек, где первая производная не существует, нет, следовательно,  x₁ = 0, x₂ = –1, x₃ = 1 – критические точки  I-го рода.

Составим  таблицу  промежутков  монотонности  функции  и определим знак производной у^/(х) в любой точке каждого промежутка.

 

х	(-∞, -1)	-1	(-1, 0)	0	(0, 1)	1	(1,+∞)
у/	–	0	+	0	–	0	+
у		0		1		0
		точка min		точка mах		точка min

 

из таблицы видно, что функция  y = x⁴ – 2x² + 1 убывает на интервалах (-∞, -1), (0, 1) и возрастает на интервалах (-1, 0) и (1, +∞)

(см. 4.5).

При переходе через критическую точку x₁ = 0 производная у^/(х) меняет знак с «плюса» на «минус», следовательно, х = 0 – точка максимума (см. 4.8 а)). При переходе через критические точки x₂ = -1 и x₃ = 1 производная у^/(х) меняет знак с «минуса» на «плюс», следовательно, х = -1 и  х = 1 точки минимума (см. 4.8 б)).

Найдем значение функции в каждой точке экстремума

 

у_mах(0) = 0⁴ – 20² + 1 = +1    М(0; +1) – точка mах,

 

у_min(1) = (1)⁴ – 2(1)² + 1 = 0    а(-1; 0) и а(1; 0) – точки min.

 

5. Найдем интервалы выпуклости (вогнутости) графика функции и точки перегиба (см. 4.9).

из производной

у^// = (у^/)^/ = (4x³ – 4x)^/ = 12x² – 4

 

найдем критические точки II-го рода, для чего приравняем к нулю производную второго порядка (см. 4.9.2)

 

у^// = 0    12x² – 4 = 0  4(3x² – 1) = 0    3x² – 1 = 0  

   

 

точек, где вторая производная не существует, нет. Следовательно,   ,    – критические точки II-го рода.

 

Составим таблицу промежутков выпуклости и вогнутости графика функции и определим знак второй производной у^//(х) в любой точке  каждого промежутка.

 

 

x
y//	+		−		+
y
		точка перегиба		точка перегиба

 

 

Из таблицы видно, что кривая выпукла на интервале   и вогнута на интервалах ,   (см. 4.9.1).

При переходе через критические точки II-го рода ,  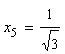  вторая производная меняет знак, а график функции

y = x⁴ – 2x² + 1

меняет направление выпуклости, следовательно, ,   – точки  перегиба графика функции (см. 4.9.2).

   

 

  и   – точки  перегиба.

 

Нанесем на числовую прямую все полученные точки х₁, х₂, х₃, х₄, х₅ и расставим на каждом полученном интервале «стрелочки»

( ,    ) и «тазики» ( ,  ).

 

 

 

Составим график функции из выделенных дуг, предварительно построив точки  М, А, В, С, Д.

 

 

Решение 

б) Воспользуемся схемой полного исследования (см. 4.10).

1.   Найдем область определения функции .

 

Функция не определена, если (х + 1) = 0, т.е. при х = -1. В остальных точках функция существует. Следовательно, область определения функции X = (-∞; -1)  (-1; +∞) (см. 4.2).