1

Обобщенные перемещения и обобщенные силы

В предыдущих разделах перемещения точек упругих тел и систем, возникающие в результате деформации, определялись как изменения значений их координат в той или иной системе координат. Указанные перемещения, которые в дальнейшем будем называть простыми перемещениями, по существу являются координатами упругой системы относительно ее начального недеформированного состояния.

При использовании многих приближенных и, в частности, вариационных методов удобнее использовать так называемые обобщенные перемещения, или обобщенные координаты.

Обобщенными перемещениями будем называть такую совокупность некоторых параметров, которой вполне определяются перемещения всех точек упругого тела или упругой системы. Обобщенные перемещения должны быть выбраны так, чтобы они были независимыми и при их произвольном изменении не нарушались связи, наложенные на систему. Приведем несколько примеров.

При вращении твердого тела вокруг неподвижной оси за обобщенное перемещение можно принять угол поворота; при вращении твердого тела вокруг неподвижной точки за обобщенные перемещения принимают три эйлеровых угла и т. п. В этих примерах число обобщенных координат равно числу степеней свободы, и располагая значениями обобщенных координат, можно определить совершенно точно положение любой точки тела.

Для упругого тела число степеней свободы бесконечно велико. Поэтому изгиб оси свободно опертой балки длиной l можно представить в виде ряда

(11.18)

Коэффициенты этого ряда можно рассматривать в качестве обобщенных координат. В самом деле, при произвольном изменении коэффициентов в выражении (11.18) на величину связи, наложенные на балку, не будут нарушены, поскольку формы обобщенных перемещений или, как их обычно называют, фундаментальные (координатные) функции удовлетворяют кинематическим условиям (обращаются в нуль на концах балки).

Из приведенных выше рассуждений следует ряд свойств, которыми должны обладать координатные функции:

1. Каждая из координатных функций должна быть непрерывной функцией координат точек в пределах непрерывной части тела или системы.

2. Каждая из координатных функций должна удовлетворять кинематическим связям системы: в точках или сечениях, где по устройству внешних связей какие-либо перемещения исключены (перемещения на жестких опорах, углы поворота сечений балки в жесткой заделке), соответствующие координатные функции или их производные должны иметь нулевые значения, в точках и сечениях, где перемещения возможны, по крайней мере одна из координатных функций (производных) должна быть отличной от нуля.

3. Совокупность всего бесконечного множества координатных функций должна образовать полную систему линейно независимых функций. Аналогично понятию обобщенного перемещения вводится понятие обобщенной силы. Обобщенные силы не могут задаваться произвольно, а должны соответствовать выбранным обобщенным координатам (перемещениям) . По определению обобщенная сила есть коэффициент при приращении обобщенного перемещения общем выражении для работы всех внешних сил, приложенных к системе, на этом перемещении

(11.19)

Пример 11.1. Пусть на свободно опертую балку действует распределенная нагрузка интенсивностью , в сечении приложена сила P, а в сечении — момент (рис. 11.4).

Решение

Для определения обобщенной силы необходимо поступить следующим образом. Дадим обобщенному перемещению приращение . Приращение вызывает приращение упругой линии балки (11.18):

Рис. 11.4. К примеру 11.1

На этом приращении указанная выше нагрузка балки произведет работу

(11.20)

Коэффициент (выражение в скобках) при будет искомым значением для обобщенной силы .

2

45. Потенциальная энергия бруса в общем случае нагружения.

Общий случай нагружения бруса , когда в поперечных сечениях возникают нормальные и поперечные силы , изгибающие и крутящие моменты одновременно .

При разгрузке тела за счет потенциальной энергии производится работа.

Упругое тело является аккумулятором энергии.

Работа силы на упругом перемещении определяется половиной произведения наибольшего значения силы и перемещения ΔL .

U = ½ P ΔL

 Если бы между силой и перемещением не было прямой пропорциональности, вместо коэффициента ½ был бы получен какой —то другой коэффициент. В частности при постоянной силе он равен единице.

Исключая из полученного для U выражения ΔL, найдем

U = P²l/2EF;

Энергия упругих деформаций стержня при изгибе определяется работой момента М на взаимном угловом перемещении dθ двух сечений.

dU = ½ M dθ

dθ = dz/ρ = Mdz/EJ_x

Если нормальная сила N меняется вдоль оси стержня, то потенциальная энергия деформации должна определяться суммированием по участкам dz. Для элементарного участка dU = N² dz /2EF, а для всего стержня

U = ^L₀∫ N² dz /2EF.

Энергетическое соотношение широко используется при определении перемещения в сложных упругих системах.

 

3

Теорема Кастильяно.

   Установим теперь метод определения перемещений, основанный на вычислении потенциальной энергии деформации. Поставим задачу нахождения перемещений точек упругой системы по направлению действия приложенных к этой системе внешних сил.

   Будем решать эту задачу в несколько приемов; сначала рассмотрим более простой случай (Рис.1), когда на балку в сечениях 1, 2, 3,... действуют только сосредоточенные силы , )... и т. д. Под действием этих сил балка прогнется по кривой и останется в равновесии.

   Прогибы сечений 1, 2, 3,..., в которых приложены силы , , ,..., обозначим , , ,... и т. д. Найдем один из этих прогибов, например — прогиб сечения, в котором приложена сила .

   Переведем балку, не нарушая равновесия, из положения в смежное положение , показанное на фиг. 328 пунктиром. Это можно сделать различными приемами: добавить новую нагрузку, увеличить уже приложенные и т. д.

   Мы представим себе, что для перехода к смежному деформированному состоянию к силе сделана бесконечно малая добавка (Рис.1); чтобы при этом переходе не нарушать равновесия, будем считать, что эта добавка прикладывается статически, т. е. возрастает от нуля до окончательного значения медленно и постепенно.

Нулевой метод компенсационный( метод измерений) - один извариантов метода сравнения с мерой, в котором на нулевой приборвоздействует сигнал, пропорциональный разности измеряемой и известнойвеличин, причем эту разность доводят до нуля. Пример: измерениеэлектрических величин (электродвижущей силы, электрического сопротивления,емкости и др.) с применением потенциометров и измерительных мостов

4

Интеграл Мора для случая растяжения-сжатия

След. »

Интеграл Мора используется для определения перемещений точек произвольных сечений элементов конструкций. Выведем интеграл Мора для случая растяжения-сжатия. Для простоты рассмотрим стержень постоянной жесткости поперечного сечения, нагруженного сосредоточенной силой F.

Определим перемещение произвольного сечения C стержня, используя теорему Кастилиано. Функция продольной силы для любого сечения этого стержня N=N(F).

Т. к. в точке С отсутствует внешняя сила, использовать напрямую теорему Кастилиано для опредления перемещения нельзя. Поэтому приложим в точке С фиктивную силу Ф.

Функция продольной силы примет вид:

N=N(F)+N₁*Ф

где N₁ – коэффициент пропорциональности.

Определим физический смысл коэффициента N₁. Для этого снимем внешнюю силу F, а фиктивную силу Ф приравняем к единице:

Функция продольной силы при F = 0, Ф = 1 будет равна:

Таким образом, N₁ – это внутренняя продольная сила, возникающая при условии разгрузки элемента конструкции от внешних сил и нагружении в точку, перемещение которой определяется, единичной безразмерной силой.

Потенциальная энергия деформации, в соответствии с формулой (3.1),

.

Для определения перемещения точки С используем теорему Кастилиано:

.

Поскольку на самом деле никакой силы в сечении C нет (т.е. Ф=0), то

.

Это выражение называется интегралом Мора и применяется для определения перемещений точек произвольных сечений элементов конструкций.

Обобщая на k-тое количество участков по N(z) и A(z), перемещение по методу Мора может быть определено:

Суть метод Мора в следующем. Если необходимо определить перемещение в заданной точке по заданному направлению, то наряду с заданной системой внешних сил в этой точке прикладывается внешнее усилие Ф = 1 в интересующим нас направлении.

        Далее составляется выражение потенциальной энергии систе­мы, состоящей из n участков с учетом одновременного действия заданной системы внешних сил и силы Ф :

                (6.1)

,

где К_х , К_у  безразмерные величины, зависящие от геометрической формы сечения и учитывают неравномерность распределения касательных напряжений в сечении при поперечном изгибе. Так, например, для прямоугольника К_х = К_у = 1,2, а для двутавра при изгибе в плоскости его стенки K = F/F_CT , где F  площадь всего сечения двутавра, F_CT  площадь стенки; N_z , Q_x  , Q_y  , M_z , M_x , M_y   внутренние силовые факторы, возникающие в поперечных сечениях заданной стержневой системы; внутренние силовые факторы, возникающие в поперечных сечениях заданной системы, от действия усилия Ф = 1.

        Дифференцируя выражение (6.1) по Ф, и полагая после этого Ф = 0, находим искомое перемещение в искомой точке в нужном направлении.

.     

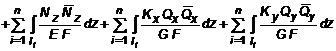5