1)предел Основные понятия. Бесконечность обозначают символом  . По сути, бесконечность   это есть либо бесконечно большое положительное число  , либо бесконечно большое отрицательное число  . Что это означает: когда Вы видите  , то не имеет разницы   это или  . Но   лучше не заменять на  , равно как и   лучше не заменять на  . Записывать предел функции f(x) принято в виде  , снизу указывается аргумент x и через стрелочку к какому значению  он стремится. Если   представляет из себя конкретное действительное число, то говорят о пределе функции в точке. Если   или  . то говорят о пределе функции на бесконечности. Сам предел может быть равен конкретному действительному числу  , в этом случае говорят, что предел конечен. Если  ,   или  , то говорят, что предел бесконечен. Еще говорят, что предел не существует, если нельзя определить конкретное значение предела или его бесконечное значение ( ,  или  ). Например, предел от синуса на бесконечности не существует. Основные определения.  Пришло время заняться нахождением значений пределов функций на бесконечности и в точке. В этом нам помогут несколько определений. Эти определения опираются на числовые последовательности и их сходимость или расходимость.  Определение (нахождение предела функции на бесконечности). Число А называется пределом функции f(x) при  , если для любой бесконечно большой последовательности аргументов функции (бесконечно большой положительной или отрицательной), последовательность значений этой функции сходится к А. Обозначается  . Замечание. Предел функции f(x) при   бесконечен, если для любой бесконечно большой последовательности аргументов функции (бесконечно большой положительной или отрицательной), последовательность значений этой функции является бесконечно большой положительной или бесконечно большой отрицательной. Обозначается  . 

  Теоремы о пределах

1. Бесконечно большие и бесконечно малые.

Функция f(x) стремится к бесконечности при x стремящимся к a, если для любого M > 0 можно указать такое значение  > 0, что для всех x удовлетворяющих неравенству xa < имеет место неравенство f(x) > M.

lim_x a=

2. Функция ограниченная при x a.

3. Функция ограниченная при x .

4. Теорема. Если lim_x a f(x)=b, то функция f(x) ограниченная при x a.

5. Бесконечно малые и их свойства. lim_x a (x)=0

Теорема. 1. Если f(x)=b+, где  - б.м. при x a, то lim_x a f(x)=b и обратно, если lim_x af(x)=b, то можно записать f(x)=b+(x).

Теорема. 2. Если lim_x a (x)=0 и (x)  0, то 1/ .

Теорема. 3. Сумма конечного числа б.м. есть б.м.

Теорема. 4. Произведение б.м. на ограниченную функцию есть б.м.

6. Теоремы о пределах.

Теорема. 1. Предел суммы есть сумма пределов.

Теорема. 2. Предел произведения есть произведение пределов.

Теорема. 3. Предел частного есть частное пределов (если знаменатель не обращается в 0).

Теорема. 4. Если u(x)  z(x)  v(x), и lim_x a u(x)=lim_x a v(x)=b, то lim_x a z(x)=b. ("Теорема о двух милиционерах").

7. Первый замечательный предел.

• 2) область определения функции;

• поведение функции на границах области определения, вертикальные асимптоты (при необходимости смотрите статью классификация точек разрыва функции);

• проверка на четность и нечетность;

• область значений функции;

• промежутки возрастания и убывания, точки экстремума;

• промежутки выпуклости (выпуклости вверх) и вогнутости (выпуклости вниз), точки перегиба (при необходимости смотрите статью выпуклость функции, направление выпуклости, точки перегиба, условия выпуклости и перегиба);

• наклонные и горизонтальные асимптоты;

• особые точки функций;

• особые свойства некоторых функций (например, наименьший положительный период у тригонометрических функций).

3) Показательная функция — математическая функция  , где   называется «основанием», а   — «показателем» степени.

Свойства

• 

• 

• 

• 

4)

5)   а)  Область определения:   D (cos x) = R .

    б)  Множество значений:   E (cos x ) = [ – 1 ,  1 ] . в)  Четность, нечетность:   функция четная.

    г)  Периодичность:   функция периодическая с основным периодом  T = 2 .

    д)  Нули функции:  cos x = 0  при   x =   +  n,   n   Z.

;

.

      з)  Экстремумы:

;             .

     График функции    y= cos x   изображен на рисунке.

6) Производной функции называется предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю

Производная, говоря простым языком, это отношение приращения функции к минимальному приращению аргумента. Совсем тяжко, то это скорость роста функции

геометрический смысл: производная функции в точке - это тангенс угла наклона касательной к графику этой функции в данной точке. 

7)физический смысл: производная функции - это скорость изменения этой функции

8) производные высших порядков Производные функции третьего и более порядков

производная от функции - первого порядка производная от первой производной - производная второго порядка производная от производной во\торого порядка - производная третьего порядка и.т.д производная десятого порядка - это производная от производной девятого порядка начиная с третьей производные называются производными высшего порядка

9) 1.      Область определения

2.      Исследование функции на четность, нечетность и периодичность

3.Нахождение точек пересечения графика функции с осями координат

4.  Нахождение промежутков знакопостоянства функции

5. Нахождение производной функции, области определения производной, критических точек

6. Нахождение промежутков возрастания, убывания, точек экстремума и экстремумов

7.  Нахождение промежутков выпуклости функции и точек перегиба

8.   Исследование поведения функции на бесконечности и в окрестности точек разрыва

9.  Построение графика (при необходимости нужно найти значения функции в дополнительных точках)

10) Первообразной функцией для функции f(x) называется такая функция F(х), производная которой равна данной функции

F'(x) = f(x).

Обозначение

где F'(x) = f(x). Функция f(x) называется подынтегральной функцией, а выражение f(x)dx - подынтегральным выражением.

11) 1°. Производная неопределенного интеграла равна подынтегральной функции; дифференциал от неопределенного интеграла равен подынтегральному выражению

2°. Неопределенный интеграл от дифференциала некоторой функции равен сумме этой функции и произвольной постоянной

3°. Постоянный множитель можно вынести из под знака интеграла, т.е. если k = const ≠ 0, то

4° . Неопределенный интеграл от алгебраической суммы двух функций равен алгебраической сумме интегралов от этих функций в отдельности.

Вычисление площадей

Пусть функция f (х)  непрерывна на отрезке [a ; b].  Если при этом f (х) ≥ 0 на [a ; b], то  площадь S криволинейной трапеции, ограниченной линиями  ,  выразится с помощью интеграла:     (1) 

Если же f (х) ≤ 0 на [a ; b], то −f (х) ≥ 0 на [a ; b].  Поэтому площадь S соответствующей  криволинейной трапеции находится по формуле    или     (2)  

Наконец, если линия у = f (х) пересекает ось Ох, то отрезок [a ; b] надо разбить на части, в  пределах которых f (х) не меняет знака, и к каждой части применить ту из формул (1) или (2),  которая ей соответств

Аксиомы

1. Аксиома 1.

Через любые три точки, не лежащие на одной прямой, проходит плоскость, и притом только одна.

2.Аксиома 2

Если две точки прямой лежат в плоскости, то все точки прямой лежат в этой плоскости

3. Аксиома 3

Если две плоскости имеют общую точку, то они имеют общую прямую, которой принадлежат все общие точки этих плоскостей.

Теорема 1.

Через прямую a и не лежащую на ней точку А проходит плоскость, и притом только одна

Теорема 2.

Через две пересекающиеся прямые a и b проходит плоскость, и при том только одна.

Теорема 3

через две паралелльные прямые проходит плоскость и притом только одна

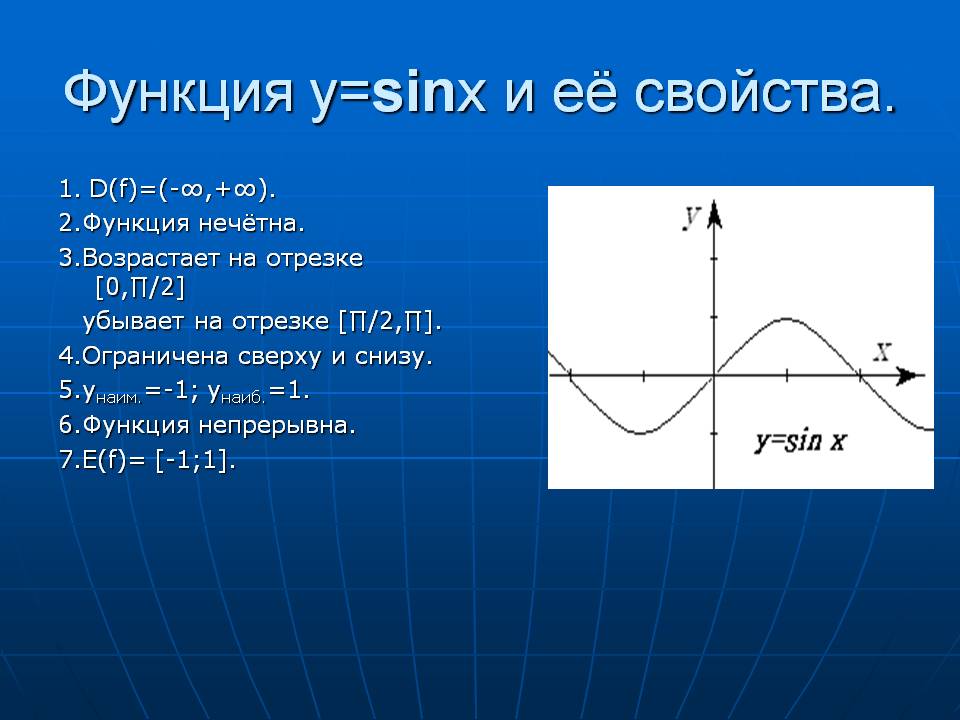
sinx

Синусом  аргумента х (sin(x)) называется ордината точки пересечения окружности единичного радиуса с центром в начале координат и луча, выходящего из начала координат и составляющего с осью ОХ угол х. Областью определения функции sin(x) является вся числовая прямая - промежуток (-?;+?). Область значений лежит в промежутке [-1;1]. Функция sin(x)  периодична, период Т = 2П. Функция sin(x)  является нечетной, так как sin(-x)=-sin(x). График функции sin(x) называют синусоидой.  Синусоида пересекает ось ОХ в точках (kП;0). Синусоида имеет экстремумы-максимумы в точках   и экстремумы-минимумы в точках  . График синусоиды:

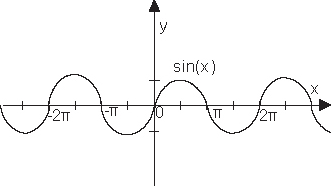
Cos

Косинусом  аргумента х (cos(x)) называется абсцисса точки пересечения окружности единичного радиуса с центром в начале координат и луча, выходящего из начала координат и составляющего с осью ОХ угол х. Областью определения функции cos(x) является  вся числовая прямая - промежуток (-?;+?). Область значений лежит в промежутке [-1;1]. Функция cos(x) периодична, период Т = 2П. Функция cos(x) является четной, так как cos(-x)=cos(x). График функции cos(x), называют косинусоидой.  Косинусоида пересекает ось ОХ в точках  .  Синусоида имеет экстремумы-максимумы в точках (2Пk;1) и экстремумы-минимумы в точках (П+2Пk;-1) График косинусоиды:

Экстремум

Найти область определения функции f(x).

Найти первую производную функции f '(x).

Определить критические точки, для этого:

найти действительные корни уравнения f '(x)=0;

найти все значения x при которых производная f '(x) не существует.

Определить знак производной слева и справа от критической точки. Так как знак производной остается постоянным между двумя критическими точками, то достаточно определить знак производной в какой-либо одной точке слева и в одной точке справа от критической точки.

Вычислить значение функции в точках экстремума.

Выпуклости

Найдём её первую и вторую производную:

Что бы найти, где вторая производная больше нуля, а где меньше, мы прировняем её к нулю и посмотрим на каких промежутках она больше, а на каких меньше:

Наносим точку x=0 на координатную прямую, и вычисляем соответствующие значения.

Точка перегиба 1. найти вторую производную

2. найти критические точки второго рода

3. исследовать знак второй производной в промежутках на которые найденые критические точки делять область определения функции

4. определить точки перегиба и найти значения в этих точках

Схема

1. Найти область определения функции.

2. Исследовать непрерывность функции, выделить особые точки (точки разрыва).

3. Проверить наличие вертикальных асимптот в точках разрыва и на границах области определения.

4. Найти точки пересечения с осями координат.

5. Установить, является ли функция чётной или нечётной. Сделать выводы о симметричности графика функции.

6. Найти первую производную. Найти точки экстремума (локального минимума и максимума) и интервалы монотонности (возрастания и убывания) функции.

7. Найти вторую производную. Найти точки перегиба и интервалы выпуклости-вогнутости.

8. Найти наклонные/горизонтальные асимптоты функции

9. Построить график функции. Построить асимптоты.