ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ

Государственное образовательное учреждение

высшего профессионального образования

ВЛАДИМИРСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

Кафедра «ВТ»

Отчет

По дисциплине: «Методы оптимизации»

На тему:

«Исследование методов решения линейных уравнений»

Выполнил студент группы ЗЭВМу – 109

Е.П. Крупнов

Принял: профессор

Жирков Владислав Федорович

Владимир 2011г.

Содержание

1. Метод ветвей и границ

2. Метод первого порядка

3. Метод второго порядка

4. Оптимальный поиск

5. Пассивный поиск

6. метод дихотомии

7. Метод золотого сечения

8. Динамическое программирование

9. Линейное программирование. Метод Жордана-Гаусса.

10. Список литературы

Метод ветвей и границ

В качестве примера метода ветвей и границ рассмотрим задачу коммивояжера.

Постановка задачи.

Имеется N пунктов, расстояние между которыми известны. Необходимо, начав движения из п.1. последовательно обойти все остальные по самому короткому пути и вернуться в п.1. Условие  заключается в следующем: в каждый пункт надо войти только один раз и один раз из него выйти. На рис.1. приведен пример задачи для N = 5. На ребрах, соединяющих вершины графа (пункты), указаны расстояния.

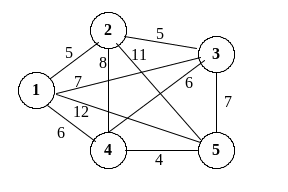
Рис. 1.

Условие  делает невозможным выбор на некотором шаге вычислений оптимального из путей, приводящих в некоторую точку. Решение задачи методом прямого перебора всех возможных (N-1)! возможно лишь для малых N, Необходим метод, который позволяет уменьшать число рассматриваемых вариантов. Таким методом является метод ветвей и границ (МВТ).

Основное содержание метода заключается в том, что строятся нижние оценки функции цели (ФЦ), позволяющие отбраковать множество вариантов, для которых значение ФЦ заведомо хуже. По мере рассмотрения новых вариантов граница перемещается вниз (в задаче минимизации) до тех пор, пока число различных вариантов не уменьшается настолько, что выбор лучшего из них будет сделан непосредственным сравнением.

Решение задачи.

Запишем исходные данные в виде таблицы C₀ = (C_ij). В ней i и j – номера пунктов, движение на каждом шаге совершается из i в j, длина этого шага пути C_ij, крестиками отмечены запрещенные переходы. Пусть С_i = min C_ij. Найдем С_i для каждого i (в таблице эти значения подчеркнуты), после чего совершим приведение матрицы С₀ к C₀¹ по строкам, где C_ij¹ вычисляются по формулам C_ij¹ = C_ij – C_i. Обозначим d₀¹ = C_i. и C_j¹ = min C_ij. Найдем C_j для всех j и выполним приведение C₀¹ по столбцам. В приведенном примере все С_j = 0, поэтому C₀² = C₀¹, константа приведения по столбцам d₀² = 0, d₀ = d₀¹ + d₀² = 23.

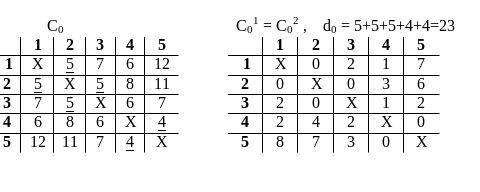
Можно утверждать, что задачам с матрицами C₀ и C₀¹ соответствует один и тот же оптимальный маршрут. Длина любого пути L_S(C₀) и L_S(C₀²) связаны формулой L_S(C₀) = L_S(C₀²) + d₀. что следует из условия . Тогда любой путь по матрице представляет движение по клеткам таблицы, причем в каждой строке и каждом столбце можно побывать только один раз.

Величину d₀ можно использовать в качестве нижней границы при оценке всех возможных путей.

Рассмотрим путь, который включает переход из i в j. Для него L_S  _ij = d₀ + C_ij. Такой переход всегда есть, так как в приведенной матрице хотя бы один элемент в строке – нулевой. Выбирая один из них, мы выбираем оптимизацию одного шага пути (самый короткий первый шаг). При этом, конечно, мы не знаем, как это отразится на длине последующего пути. Обозначим (ij) множество путей, не содержащих непосредственный переход из i в j. Поскольку из i надо куда-то выйти, а в j откуда-то прийти, то этому множеству соответствует оценка:

L_S  _(ij) = d₀ + _ij, где _ij =

Тогда нижней оценкой для множества путей будет ₂ = d₀ + _ij. Мы заинтересованы в выборе такого перехода ij, для которого эта оценка является самой высокой. Этот выбор можно сделать, отыскав среди нулевых элементов i строки такой, которому соответствует ² = max _ij. Выбором пары (ij) все множество возможных путей разбивается на два подмножества. Одно из них содержит переход (ij) (ему соответствует оценка ₁ = d₀ + ¹), другое (ij) (ему соответствует оценка ₂ = d₀ + ²).

В нашем примере первым шагом пути должен быть переход из п.1. С_ij= 0 для i,j = 1,2. Множество всех возможных путей  разбиваем на два: содержащих переход (12) и не содержащих переход (12). Строим для них нижние оценки. ₁ = d₀ = 23. Для перехода, не содержащего (12), соответствует путь, содержащий переходы (14) и (32). На этом первая итерация вычислительного процесса заканчивается. При дальнейшем движении за поиском оптимального пути будем наблюдать с помощью дерева вариантов (рис.2).

Рис. 2.

Рассмотрим теперь первое подмножество. В нем уже реализован переход (12), поэтому в таблице С₀² строку 1 и столбец 2 удаляем (вычеркиваем) из дальнейшего рассмотрения. С₀² преобразуется в С₁, а после приведения – в С₁². В верхнем левом углу таблицы С₁ ставим крестик, так как переход (21) в рассматриваемом подмножестве (12) становиться невозможным.

Теперь над новой таблицей проделываем те же действия, что и над С². Для С₁² константа приведения ₁ = 2. Далее в качестве возможных рассмотрим подмножества, содержащие пути (23) и ( ), и произведем их оценку:

(23) ₂₃ = ₁ = (d₀ + d₁₎ + с₂₃ = 23 + 2 + 0 = 25.

( ) = ₂ = (d₀ + d₁₎ + ₂₃ = 25 + 5 = 30,

где ₂₃ = = C₂₄ + C ₄₃ = 3+2 = 5.

После вычеркивания из таблицы C₁² строки i = 2 и столбца j = 3 получается матрица С₂ размером 3х3. Очередное разбиение возможных вариантов перемещения на подмножестве (34) и ( ) дает оценки ₃₄ = 26 и =27.

После очередного сокращения матрицы таблица принимает размер 2х2 и однозначно определяет путь: начальная точка 4, конечная – 1, путь (451). Он имеет длину 6. По дереву вариантов мы прошли путь до вершины. Длинный путь (123451) имеет длину 32. Аналогично множество ( ) содержит единственный путь (3541) длиной 2. Путь (123541) имеет длину 27, его длина меньше, чем у пути, содержащего переход (34). В качестве нижней границы теперь следует выбирать 27. Любое множество, имеющее оценку больше 27, следует отбросить. Если же оценка меньше 27, то такой путь подлежит исследованию. Если, пройдя по новому пути, получим значение длины меньше 27, то это новое значение следует взять в качестве новой оценки. Итак, мы прошли по дереву вариантов до вершины и длину одного их путей используем для последующей оценки вариантов.

Возвращаемся теперь по дереву вверх до ближайшего узла (12). Не рассмотренная ветвь дерева ( ) имеет нижнюю оценку 30, что хуже достигнутого результата. Значит, эту ветвь можно далее не исследовать. Переходим к ветви ( ). Оценка для этой ветви ниже 27, поэтому данное множество следует рассмотреть.

В результате исследования придем к результату, что оптимальный путь (123541).

Сравним теперь данный метод с динамическим программированием. В ДП на очередном шаге выбирается самый короткий путь, ведущий в данную точку; все остальные пути исключаются из дальнейшего рассмотрения. В МВГ при разбиении также рассматривается самый короткий путь, содержащий переход (ij) и множество остальных путей ( ). Но, в отличии от ДП, мы не может множество (ij) исключить из дальнейшего рассмотрения. В процессе последовательного разбиения, двигаясь от корня к одной из вершин, необходимо запомнить в каждом из узлов информацию для последующего анализа множества возможных путей при возврате от вершины к корню дерева. Следует отметить, что МВГ весьма экономичен с точки зрения требуемой памяти. Если решение задачи метод ветвей и границ прервать (например, по истечении отведенного времени), то хотя оптимальное решение не будет достигнуто, в памяти будет храниться одно из возможных решений. В динамическом программировании решение получается только на последнем шаге вычислительного процесса (оно же и оптимальное).

Из изложенного следует сделать вывод, что МВГ - весьма эффективный метод, с помощью которого можно решать разнообразные задачи с аддитивной целевой функцией.

Листинг программы

var

Way:TVector;

LengthOfWay:real;

HightLimitWasSeted:boolean;

function Addiction(var Matrix:Tarray;SizeOfMatrix:integer):real;

var

MinInRow,MinInCol:real;

i,j:integer;

d1,d2,d:real;

function MinElInRow(NumRow:integer):real;

var

i:integer;

min:real;

index:integer;

begin

index:=0;min:=1e38;

for i:=1 to SizeOfMatrix do

if (Matrix[NumRow,i]<min) then begin

min:=Matrix[NumRow,i];index:=i

end;

if index=0 then raise Error;

MinElInRow:=min

end;

function MinElInCol(NumCol:integer):real;

var

i:integer;

min:real;

index:integer;

begin

index:=0;min:=1e38;

for i:=1 to SizeOfMatrix do

if (Matrix[i,NumCol]<min) then begin

min:=Matrix[i,NumCol];index:=i

end;

if index=0 then raise Error;

MinElInCol:=min

end;

begin

d1:=0;

for i:=1 to SizeOfMatrix do

begin

MinInRow:=MinElInRow(i);

d1:=d1+MinInRow;

for j:=1 to SizeOfMatrix do

Matrix[i,j]:=Matrix[i,j]-MinInRow;

end;

d2:=0;

for i:=1 to SizeOfMatrix do

begin

MinInCol:=MinElInCol(i);

d2:=d2+MinInCol;

for j:=1 to SizeOfMatrix do

Matrix[j,i]:=Matrix[j,i]-MinInCol;

end;

d:=d1+d2;

Addiction:=d

end;

procedure FindBestWay(var matrix:TArray;SizeOfMatrix:integer;basis:integer;LowLimit:real);

var

LessMatrix:Tarray;

LowLimit1,LowLimit2:real;

i:integer;

d:real;

NextPoint:integer;

SpareDistance:real;

Row,Column:integer;

min1,min2,min:extended;

procedure Print;

var

i,j:integer;

number:integer;

s:string;

begin

for i:=1 to SizeOfMatrix do

begin

for j:=1 to SizeOfMatrix do

begin

if Matrix[i,j]>Maxint then s:=' X '

else Str(Round(Matrix[i,j]):3,s);

Text:=Text+s+' '

end;

Text:=Text+#13+#10

end;

Text:=Text+#13+#10

end;

procedure FindNextPoint(var BestPointAfterBasis:integer;var SpareDistance:real);

var

min1,min2:real;

i:integer;

RowOfBasis,BestColumn:integer;

begin

for i:=1 to SizeOfMatrix do

if Round(Matrix[i,0])=basis then

begin

RowOfBasis:=i;

break

end;

for i:=1 to SizeOfMatrix do

if Matrix[RowOfBasis,i]=0 then

begin

BestColumn:=i;

BestPointAfterBasis:=Round(Matrix[0,i]);

break

end;

min1:=1e38;

for i:=1 to SizeOfMatrix do

if (i<>BestColumn) and (Matrix[RowOfBasis,i]<min1) then

min1:=Matrix[RowOfBasis,i];

min2:=1e38;

for i:=1 to SizeOfMatrix do

if (i<>RowOfBasis) and (Matrix[i,BestColumn]<min2) then

min2:=Matrix[i,BestColumn];

SpareDistance:=min1+min2;

end;

procedure FormLessMatrix(From,T0:integer);

var

i,j:integer;

ii,jj:integer;

RowOfFrom,ColumnOfTo,Row:integer;

begin

for i:=1 to SizeOfMatrix do

if Round(Matrix[i,0])=From then

begin

RowOfFrom:=i;

break

end;

for i:=1 to SizeOfMatrix do

if Round(Matrix[0,i])=T0 then

begin

ColumnOfTo:=i;

break

end;

for i:=0 to SizeOfMatrix-1 do

for j:=0 to SizeOfMatrix-1 do

begin

if i>=RowOfFrom then ii:=i+1

else ii:=i;

if j>=ColumnOfTo then jj:=j+1

else jj:=j;

LessMatrix[i,j]:=Matrix[ii,jj]

end;

for i:=1 to SizeOfMatrix-1 do

if Round(LessMatrix[i,0])=T0 then

begin

Row:=i;

break

end;

if Row<=SizeOfMatrix-1 then LessMatrix[Row,1]:=1e38

end;

begin

Print;

if SizeOfMatrix=2 then

begin

min1:=Matrix[1,2]+Matrix[2,1];

min2:=Matrix[1,1]+Matrix[2,2];

if min1<min2 then min:=min1

else min:=min2;

LengthOfWay:=LowLimit+min;

if LengthOfBestway>LengthOfWay then

begin

inc(Way.CountOfPoints);

Way.Points[Way.CountOfPoints]:=Round(Matrix[0,2]);

LengthOfBestWay:=LengthOfWay;

BestWay:=Way;

dec(Way.CountOfPoints);

end;

if not(HightLimitWasSeted) then

begin

HightLimitWasSeted:=true;

HightLimit:=LengthOfWay

end;

end

else if SizeOfMatrix>2 then

begin

inc(Way.CountOfPoints);

repeat

FindNextPoint(NextPoint,SpareDistance);

Way.Points[Way.CountOfPoints]:=NextPoint;

FormLessMatrix(Basis,NextPoint);

d:=Addiction(LessMatrix,SizeOfMatrix-1);

LowLimit1:=d+LowLimit;

LowLimit2:=LowLimit+SpareDistance;

FindBestway(LessMatrix,SizeOfMatrix-1,NextPoint,LowLimit1);

if LengthOfBestWay>=LowLimit2 then

begin

for i:=1 to SizeOfMatrix do

if Round(Matrix[i,0])=Basis then

begin

Row:=i;

break

end;

for i:=1 to SizeOfMatrix do

if Round(Matrix[0,i])=NextPoint then

begin

Column:=i;

break

end;

Matrix[Row,Column]:=1e38;

Addiction(Matrix,SizeOfMatrix);

LowLimit:=LowLimit2

end

until LengthOfBestWay<=LowLimit2;

dec(Way.CountOfPoints);

end

else raise Error

end;

begin

LengthOfBestWay:=1e38;

Way.CountOfPoints:=1;

Way.Points[1]:=1;

Text:='';

d0:=Addiction(MatrixOfLinking,n);

HightLimitWasSeted:=false;

FindBestWay(MatrixOfLinking,n,1,d0)

end;

end.