Одноканальные и многоканальные смо с пуассоновским входным потоком и экпотенциальным распределением длительности обслуживания

Поток событий – это последовательность однородных событий, которые наступают (следуют одно за другим, происходят) в некоторые случайные моменты времени. Основная характеристика потока событий – его интенсивность λ - среднее число событий, поступающих в СМО в единицу времени.

Поток событий называется простейшим (или стационарным пуассоновским), если он одновременно стационарен, ординарен и не имеет последействия.

Основные количественные характеристики простейшего потока.

Изобразим на оси времени Ot простейший поток событий как последовательность случайных n точек на достаточно большом отрезке длиной T >>1, для которых справедливы следующие предположения:

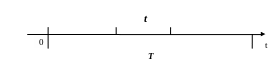
Рис.3

2. на единицу длины в среднем приходится λ точек, что соответствует интенсивности потока, т.е. λ = ;

3. вероятность расположения того или иного числа точек на отрезке длиной t зависит только от его длины и не зависит от его расположения на оси, что соответствует равновозможности событий в потоке и отсутствию последействия;

4. точки располагаются на оси независимо друг от друга, что соответствует независимости событий в потоке, а также отсутствию последействия.

Определим вероятность того, что ровно m точек окажется на отрезке длиной t.

Согласно первому предположению на отрезке T расположено n=λT точек, причём каждая из них может оказаться в любом месте отрезка T (в силу 2-ого 3-его предположения) и все эти положения равновозможные. Вероятность, что одна из этих точек окажется на отрезке t, равна p = t/T и согласно 2-ому предположению не зависит от того, какая это точка: первая, вторая или иная.

В результате мы приходим к схеме Бернулли:

производится n испытаний, в каждом из которых мы следим за одной точкой, и любые из эти точек с вероятностью p могут оказаться на отрезке t . Поэтому вероятность того, что ровно m точек из n окажутся на отрезке t определяется по формуле Бернулли:

,

где .

При неограниченном увеличении длины отрезка T→∞ , т.е. при неограниченной последовательности случайных точек (бесконечный поток событий), n = λT→ ∞, а p= →0, но при этом np = λT· = λt остаётся постоянной, т.к. λ и t константы. Следовательно, можно применить формулу Пуассона, которая в данном случае является точной, а не асимптотической:

Итак, бесконечный поток событий называется простейшим, пуассоновским, если вероятность p_t(m) появления ровно m событий за время t определяется формулой Пуассона:

, где m! = 1 2 3....m, (2.1.1.)

для которого математическое ожидание (среднее число событий потока за время t при его интенсивности λ) равно его дисперсии: M(m) = σ² = λt.

Из (2.1.1), в частности, следует, что вероятность того, что за время t не произойдёт ни одного события (m=0), равна:

P_t(0) = e^-λt. (2.1.2)