Билет 15
Всякое каким-то образом выделенное множество объектов, которые могут отличаться друг от друга значением некоторой определенной характеристики, называется генеральной совокупностью.
Число элементов генеральной совокупности называется ее объемом.
Часть генеральной совокупности, случайным образом отобранная для наблюдений, называется случайной выборкой или, для краткости, выборкой.
Число элементов выборки называется ее объемом.
Так, если из ста тысяч упаковок некоторого лекарства (генеральная совокупность) для контроля качества отобрано сто упаковок (выборка), то объем генеральной совокупности составляет 100000, а объем выборки – 100.
Свойства выборочной совокупности тем лучше отражают соответствующие свойства генеральной совокупности, чем больше объектов содержит эта выборочная совокупность (т.е. чем больше ее объем). Например, если интересует концентрация некоторого вещества в таблетках, выпускаемых при помощи аппарата определенной конструкции, то чем больше случайным образом отобранных таблеток мы исследуем, тем более достоверную информацию получим.
Поскольку мы рассчитываем с помощью статистических методов высказать определенное суждение о свойствах генеральной совокупности по свойствам выборки, то последняя должна быть репрезентативной (представительной), т.е. должна быть организована таким образом, чтобы, по возможности, отражать все интересующие нас свойства генеральной совокупности.
Например, при обследовании на предмет успеваемости по физиологии студентов медицинских университетов А, В и С, в которых обучаются 500, 200 и 300 студентов соответственно, выборку объемом 100 следует строить так, чтобы в нее входило 50 случайным образом выбранных студентов университета А, 20 студентов университета В и 30 студентов университета С. Пропорции в выборке должны соответствовать пропорциям генеральной совокупности.
Для обеспечения репрезентативности выборка должна быть достаточно объемной с тем, чтобы охватывать всю генеральную совокупность, и производиться беспристрастно по отношению к отдельным ее частям.
Повторной называют выборку, при которой отобранный объект (перед отбором следующего) возвращается в генеральную совокупность. Бесповторной называют выборку, при которой отобранный объект в генеральную совокупность не возвращается. На практике обычно пользуются бесповторным случайным отбором.
На практике применяются различные способы отбора. Принудительно эти способы можно подразделить на два вида:
I. Отбор, не требующий расчленения генеральной совокупности на части, сюда относятся:
а) простой случайный бесповторный отбор;
б) простой случайный повторный отбор.
II. Отбор, при котором генеральная совокупность разбивается на части, сюда относятся:
а) типический отбор;
б) механический отбор;
в) серийный отбор.
Простым случайным называют такой отбор, при котором объекты извлекают по одному из всей генеральной совокупности. Если извлеченные карточки не возвращать в пачку, то выборка будет простой случайной бесповторной.
Типическим называют отбор, при котором объекты отбираются не из всей генеральной совокупности, а из каждой ее «типической» части.
Механическим называют отбор, при котором генеральная совокупность «механически» делится на столько групп, сколько объектов должно войти в выборку, и из каждой группы отбирается один объект.
Серийным называют отбор, при котором объекты отбирают из генеральной совокупности не по одному, а «сериями», которые подвергаются сплошному обследованию.
Графически можно отложить ординаты
длины
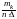в абсциссах xk.
Далее появляются две возможности: можно
либо соединить полученные точки ломаной
линией – получим полигон частот
(рис. 5), либо провести через них
горизонтальные отрезки – получим
гистограмму (рис. 6).
Рис. 5. Полигон частот. y1 x1 x2 xn yn x
y1 x1 x2 xn yn x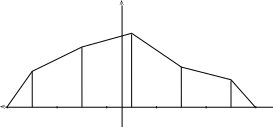 
|
Рис. 6. Гистограмма. 
|
Полигон и гистограмма и дают приближение для плотности p(x). Закон больших чисел Бернулли и общеизвестные теоремы математического анализа позволяют утверждать, что в точках непрерывности плотности p(x) отклонения от неё гистограммы и полигона будут как угодно малы со сколь угодно большой вероятностью при достаточно больших n и N и достаточно малом . Нужно помнить, что, с одной стороны, нужно делать малым, чтобы уменьшить ошибку от замены интеграла площадью ступеньки, а с другой стороны, нельзя взять слишком малым, чтобы не увеличить вероятностную ошибку от замены вероятности на относительную частоту.
Эмпирическая функция распределения (выборочная функция распределения) — естественное приближение теоретической функции распределения данной случайной величины, построенное по выборке.
Пусть известно статистическое распределение частот количественного признака Х. Введем обозначения: nх - число наблюдений, при которых наблюдалось значение признака меньшее x1, n – общее число наблюдений (объем выборки). Ясно, что относительная частота события Хх/n. Если х будет изменяться, то, вообще говоря, будет, меняться и относительная частота, т.е. относительная частота nх/n есть функция от х. Так как эта функция находится эмпирическим (опытным) путем, то ее называют эмпирической.
Эмпирической функцией распределения (функцией распределения выборки) называют функцию F*(x), определяющую для каждого значения х относительную частоту события Х
F*(x)=nх/n
где nх – число вариант, меньшее х, n – объем выборки
Таким образом, для того, чтобы найти, например F*(x2), надо число вариант, меньшее x2, разделить на объем выборки n: F*(x2)=nх2/n
В отличие от эмпирической функции распределения выборки, интегральную функцию F(x) распределения генеральной совокупности называют теоретической функцией распределения. Различие между эмпирической и теоретической функциями состоит в том, что теоретическая функция F(x) определяет вероятность события Х Из определения функции F*(x) вытекают следующие ее свойства:
1. Значения эмпирической функции принадлежат отрезку [0;1]
2. F*(x) - неубывающая функция
3. Если х1 – наименьшая варианта, то F*(x)=0 при х≤х1; если хk – наибольшая варианта, то F*(x)=1 при х>хk.
Итак, эмпирическая функция распределения выборки служит для оценки теоретической функции распределения генеральной совокупности.