
- •1.Силы, действующие в атмосфере. Массовые и поверхностные силы.
- •2.Особенности проявления силы тяжести в атмосфере.
- •3.Особенности проявления силы Кориолиса в атмосфере.
- •4.Особенности проявления поверхностных сил в атмосфере.
- •5. Тензор упругих напряжений. Связь с вязкостью.
- •7. Индивидуальная и локальная производные. Что изменяется в ур-ниях движения?
- •16.Число гомохронности. Пример применения
- •17. Число Фруда. Пример применения
- •18. Число отклонения от геострофичности. Пример применения
- •19. Число Эйлера. Пример применения
- •20. Число Рейнольдса. Пример применения.
- •22. Определение n- мерного векторного пространства. Свойства.
- •23. Скалярное произведение векторов. Пример в д. Метеорологии.
- •24.Векторное произведение векторов. Пример в динам. Метеорологии
- •Понятие тензора. Пример в динам. Метеорологии
- •27. Ковариантное и контравариантное преобразование
- •28. Уравнение статики. Однородная атмосфера
- •29. Уравнение статики. Политропная атмосфера
- •30. Интегрирования уравнения статики. Барометрические формулы.
- •31. Геопотенциал. Абсолютная и относительная топография.
- •32.Ветер в свободной атмосфере. Гидростатическое и геострофическое приближения.
- •33.Геострофический и градиентный ветер. Линейка Пагосяна.
- •34.Баланс сил в циклоне и антициклоне. Выражения для скорости ветра.
- •36) Выражение и физический смысл дивергенции и ротора в натуральных координатах
- •38) Уравнение Пуассона
- •39) Понятие о потенциальной температуре
- •40. Условие вертикальной устойчивости. Сухоадиабатический градиент.
- •41. Сжатие или расширение воздушного столба. Адвекция тепла и адвекция холода.
- •42. Термодинамические процессы во влажном ненасыщенном воздухе. Виртуальная температура.
- •43. Термодинамические процессы во влажном насыщенном воздухе. Температура точки росы. Высота конденсации. Отношение смеси.
- •44. Понятие и расчет энергии неустойчивости. Мощность конвекции.
- •45.Влажноадиабатический градиент. Последовательность развития конвекции.
- •46. Использование термодинамических графиков. Эквивалентная температура.
- •47. Волновые движения в атмосфере. . Продольные и поперечные волны.
- •49.Процессы, приводящие к движению в атмосфере. Преобразование энергии.
- •51.Взаимодействие глобальных и местных циркуляционных ячеек.
22. Определение n- мерного векторного пространства. Свойства.
Векторное пространство называют. n-мерным (или имеет «размерность n»), если в нём существуют n линейно независимых элементов e1, e2, ...en, а любые n+1 элементов линейно зависимы. Векторное пространство называют бесконечномерным, если в нём для любого натурального n существует n линейно независимых векторов. Любые n линейно независимых векторов n-мерного векторного пространства образуют базис этого пространства. Если e1, e2, ...en - базис векторного пространства, то любой вектор x этого пространства может быть представлен единственным образом в виде линейной комбинации базисных векторов: x = α1e1 + α2e2 + ... + αnen. При этом числа α1, α2, ...,αn называют координатами вектора x в данном базисе.
Примеры векторных пространств:
Множество всех векторов 3-мерного пространства образует векторное пространство. Более сложным примером может служить так называемое n-мерное векторное пространство. Векторами этого пространства являются упорядоченные системы из n действительных чисел (λ1, λ2, ..., λn). Сумма двух векторов и произведение на число определяются соотношениями: (λ1, λ2, ..., λn) + (μ1, μ2, ..., μn) = = (λ1 + μ1, λ2 + μ2, ..., λn + μn), α∙(λ1, λ2, ..., λn) = (α∙λ1, α∙λ2, ..., α∙λn). Базисом в этом пространстве может служить, например, следующая система из n векторов: e1 = (1, 0, ..., 0), e2 = (0, 1, ..., 0), ...en = (0, 0, ..., 1).
Множество L всех многочленов α0 + α1u + ... + αnun (любых степеней n) от одного переменного с действительными коэффициентами α0, α1, ..., αn с обычными алгебраическими правилами сложения многочленов и умножения многочленов на действительные числа образует векторное пространство. Многочлены 1, u, u2, ..., un (при любом n) линейно независимы в L, поэтому L - бесконечномерное векторное пространство. Многочлены степени не выше n образуют векторное пространство размерности n+1; его базисом могут служить многочлены 1, u, u2, ..., un.
23. Скалярное произведение векторов. Пример в д. Метеорологии.
Скаля́рное произведе́ние— операция над двумя векторами, результатом которой является число (скаляр), не зависящее от системы координат и характеризующее длины векторов-сомножителей и угол между ними. Данной операции соответствует умножение длины данного вектора а на проекцию другого вектора b на данный вектор а.
![]()
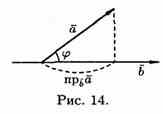
Из
ф-лы следует, что
![]() ,
если
,
если
![]() -
острый угол,
-
острый угол,
![]() ,
если
-
тупой угол;
,
если
-
тупой угол;
![]() в
том и только в том случае, когда векторы
в
том и только в том случае, когда векторы
![]() и
и
![]() перпендикулярны
(в частности,
,
если
перпендикулярны
(в частности,
,
если
![]() или
или
![]() ).
).
Для любых векторов a, b и c и любого числа λ справедливы равенства:
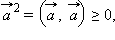 причем
причем
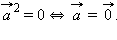
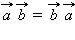 (переместительный
закон).
(переместительный
закон).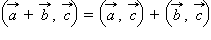 (распределительный
закон).
(распределительный
закон).
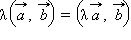 (сочетательный
закон).
(сочетательный
закон).
Если векторы и заданы своими координатами:
![]() ,
,
![]() ,
,
то их скалярное произведение может быть вычислено по формуле
![]() .
.
Отсюда следует необходимое и достаточное условие перпендикулярности двух векторов
![]() .
.
Угол между векторами
, ,
дается
формулой
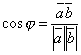 ,
или в координатах
,
или в координатах
![]() .
.
