8.6.1. Критерий согласия 2 (критерий Пирсона)

Этот критерий является важнейшим из , применяемых на практике. Предположим, что, как это изложено в п.8.2. , построены выборочные гистограммы плотности вероятности и кроме того имеется график плотности вероятности гипотетического распределения. Обозначим: p_i - вероятность попадания случайного числа X в i-й класс; n_i - выборочная частота попадания случайной величины X в i-й класс. Предполагается, что величины p_i взяты из данных для гипотетического распределения. Таким образом p₁+p₂+. . .+p_k =1 и n₁+n₂+. . .+n_k= n . Здесь k - число классов (столбцов) гистограммы; n - размер выборки. Теоретическая частота попадания случайной величины в i-й класс очевидно равна p_i^.n. В качестве меры отклонения распределения выборки от гипотетического можно принять следующую случайную величину (статистику):

.

Данная статистика асимптотически (т.е. при n  ) имеет распределение ² с (k-1) степенью свободы, и не зависит от гипотетического распределения. Это утверждение доказано К. Пирсоном.

Критерий применяется следующим образом. Делается n наблюдений случайной величины X . Область полученных значений X разбивается на классы необязательно одинаковой ширины таким образом, чтобы число наблюдений в каждом классе n_i было достаточно велико. В литературе имеются различающиеся рекомендации по минимальному числу таких наблюдений от 4 до 10. Если же некоторые n_i слишком малы, то перед применением критерия целесообразно объединить такие классы. Если же выборка очень мала, то критерием пользоваться не следует. Строится выборочная функция плотности распределения. Принимается гипотетическая функция плотности. Далее выбирается уровень значимости , подсчитывается величина X² и сравнивается с квантилью ²_{(1-), k-1}. Если X² > ²_{(1-), k-1} , то гипотетическое распределение отвергается.

Приведенная выше формула для X² обладает одной особенностью. Дело в том, что она требует, чтобы гипотетическая функция плотности распределения была полностью известна. На практике чаще бывает известен лишь общий вид этой функции, а параметры от которых она зависит как правило неизвестны и могут быть получены лишь на основе выборочных данных. Например, если в качестве гипотетической функции взять функцию плотности нормального распределения , то ее параметры - математическое ожидание и стандартное отклонение могут быть неизвестны заранее и оценены лишь про результатам статистической обработки выборки.

Р.Фишер показал, что в случае r неизвестных параметров гипотетического распределения можно воспользоваться их статистическими оценками для определения p_i в формуле для X² , но полученное таким образом значение X² будет подчиняться ХИ-квадрат распределению с f=k - r -1 степенями свободы. Таким образом число степеней свободы распределения X² уменьшается на число r неизвестных параметров гипотетического распределения. При этом r < k, а статистические оценки параметров должны быть получены методом максимального правдоподобия.

Примечание. Суть метода максимального правдоподобия заключается в том, что в качестве оценки для параметра , выбирается такая величина, которая доставляет функции правдоподобия максимум. Рассмотрим x₁, x₂,... x_n выборочные n значений случайной величины X с плотностью вероятности f(x,), зависящей от неизвестного параметра . Указанную выборку следует рассматривать как многомерную случайную величину c взаимно независимыми компонентами x₁, x₂,... x_n. Функцией правдоподобия называется плотность распределения этой многомерной случайной величины.

L(x₁, x₂,... x_n,)=f(x₁,) f(x₂,)... f(x_n,).

Для нахождения параметра  нужно решить уравнение dL/d=0.

Пример 8.7. Рассмотрим для условий примера 8.2 сходство полученного в нем эмпирического распределения с гипотетическим нормальным распределением. При этом используем выборочные значения среднего равное 3,85, которое совпадает с оценкой максимального правдоподобия. Для дисперсии оценка максимального правдоподобия будет отличаться от полученной в примере 8.2. Ее можно получить, если в формуле для дисперсии использовать в качестве знаменателя общую длину выборки n=50. Полученное в результате стандартное отклонение равно 1,126.

Учитывая, что в первом и седьмом классах гистограммы число наблюдаемых величин мало мы объединим их с соседними и в результате получим пять классов и соответственно число степеней свободы для ХИ-квадрат распределения будет равно f=5-2-1=2. Для вычисления гипотетических вероятностей попадания случайных величин в классы воспользуемся таблицами вероятности нормального распределения. Результаты представим в табл.8.6.

Таблица 8.6.

Классы	Частота попа- дания в класс ni	Гипотетическая вероятность pi	n.pi=50.pi	(ni - n.pi)2 n.pi
0,512,51	5	0,117	5,85	0,123
2,513,51	14	0,265	13,25	0,042
3,514,51	18	0,339	16,95	0,065
4,515,51	10	0,209	10,45	0,019
5,517,51	3	0,069	3,45	0,059

Суммируя данные последнего столбца получим X² = 0,308. По таблице ХИ-квадрат распределения для двух степеней свободы и уровня значимости 0,2 находим квантиль ²_{0,8; 2}= 3,22. Это означает, что с доверительной вероятностью 0,8 эмпирическое распределение согласуется с нормальным. На нижеследующем рисунке изображены гистограммы выборочной (сплошная линия) и гипотетической (штриховая линия) плотности распределения.

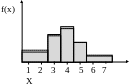
Рис.8.3. Гистограмма плотности вероятности