Билет №18

1.Дифракция Фраунгофера на дифракционной решетке

Большое практическое значение имеет дифракция, наблюдаемая при прохождении света через одномерную дифракционную решетку- систему параллельных щелей равной ширины, лежащих в одной плоскости и разделенных равными по ширине непрозрачными промежутками. Рассматривая дифракцию Фраунгофера на щели, мы видели, что распределение интенсивности на экране определяется направлением дифрагированных лучей. Это означает, что перемещение щели параллельно самой себе

влево или вправо не изменит дифракционной картины. Следовательно, если перейти от одной щели ко многим (к дифракционной решетке), то дифракционные картины, создаваемые каждой щелью в отдельности, будут одинаковыми.

Дифракционная картина на решетке определяется как результат взаимной интерференции волн, идущих от всех щелей, т.е. в дифракционной решетке осуществляется многолучевая интерференция когерентных дифрагированных пучков света, идущих от всех щелей.

Рассмотрим дифракционную решетку. На рис. для наглядности показаны только две соседние щели MN и CD. Если ширина каждой щели равна a , а ширина непрозрачных участков между щелями b, то величина d = a + b называется постоянной (периодом) дифракционнойрешетки. Пусть плоская монохроматическая волна падает нормально к плоскости решетки. Так как щели находятся друг от друга на одинаковых расстояниях, то разности хода лучей, идущих от двух соседних щелей, будут для данного направления одинаковы в пределах всей дифракционной решетки: Δ = CF = (a + b)*sinφ = d sinφ .

Очевидно, что в тех направлениях, в которых ни одна из щелей не распространяет свет, он не будет распространяться и при двух щелях, т.е. главные минимумы интенсивности будут наблюдаться в направлениях, определяемых условием: a sinφ = mλ,

(m = ±1,±2,±3,…).

Кроме того, вследствие взаимной интерференции световых лучей, посылаемых двумя щелями, в некоторых направлениях они будут гасить друг друга, т.е. возникнут дополнительные минимумы.

Очевидно, что эти дополнительные минимумы будут наблюдаться в тех направлениях, которым соответствует разность хода лучей λ / 2 , 3λ / 2 , ..., посыпаемых, например, от крайних левых точек M и C обеих щелей. Таким образом, с учетом условие дополнительных минимумов: d sin φ =(2m+1)λ/2 (m = 0,±1,±2,±3,…).

Наоборот, действие одной щели будет усиливать действие другой, если d sin φ =mλ (m = 0,±1,±2,±3,…). т.е. выражение задает условие главных максимумов.

Таким образом, полная дифракционная картина для двух щелей определяется из условий:

d sin φ = λ, 2λ, 3λ,…,… - главные минимумы;

d sin φ = λ/2, 3λ/2, 5λ/2 - дополнительные минимумы;

d sin φ = 0, λ, 2λ, 3λ,… - главные максимумы, т.е. между двумя главными максимумами располагается один дополнительный минимум.

Аналогично можно показать, что между каждыми двумя главными максимумами при трех щелях располагается два дополнительных минимума, при четырех щелях- три и т.д.

Если дифракционная решетка состоит из N щелей, то условием главных минимумов является условие, условием главных максимумов - условие, а условием дополнительных минимумов

d sin φ=m’λ/N; (m’= ±1,±2,…,±N -1, ±N +1, …, ±2N -1, ±2N +1,…), где m’ может принимать все целочисленные значения, кроме 0,±N, ±2N,…, т.е. кроме тех, при которых условие переходит в . Следовательно, в случае N щелей между двумя главными

максимумами располагается N -1 дополнительных минимумов, разделенных вторичными максимумами, создающими весьма слабый фон.

Чем больше щелей N , тем большее количество световой энергии пройдет через решетку, тем больше минимумов образуется между соседними главными максимумами, тем, следовательно, более интенсивными и более острыми будут максимумы. На рис. качественно представлена дифракционная картина от восьми щелей. Так как модуль sinφ не может быть больше единицы, то из следует, что число главных максимумов m < d /λ, т.е. определяется отношением периода решетки к длине волны.

Положение главных максимумов зависит от длины волны λ. Поэтому при пропускании через решетку белого света все максимумы, кроме центрального (m = 0), разложатся в спектр, фиолетовая область которого будет обращена к центру дифракционной картины, красная- наружу. Это свойство дифракционной решетки используется для исследования спектрального состава света (определения длин волн и интенсивностей всех монохроматических компонентов), т.е. дифракционная решетка может быть использована как спектральный прибор.

Дифракционные решетки, используемые в различных областях спектра, отличаются размерами, формой, материалом поверхности, профилем штрихов и их частотой (от 6000 до 0,25 штрих/мм, что позволяет перекрывать область спектра от ультрафиолетовой его части до инфракрасной). Например, ступенчатый профиль решетки позволяет концентрировать основную часть падающей энергии в направлении одного определенного ненулевого порядка.

2. Свободная частица — частица, движущаяся в отсутствие внешних полей. Так как на свободную частицу (пусть она движется вдоль оси х) силы не действуют, то потенци­альная энергия частицы U(x) = const и ее можно принять равной нулю. Тогда полная энергия частицы совпадает с ее кинетической энергией. В таком случае уравнение Шредингера (217.5) для стационарных состояний примет вид                                                  

Прямой подстановкой можно убедиться в том, что частным решением уравнения) является функция y(х) = Ае^ikx , где А = const и k = const, с собственным значением энергии                                                                       

Функция  представляет собой только координатную часть волновой функции Y(x, t). Поэтому зависящая от времени волновая функция, согласно (217.4),                                          (219.3)

(здесь  и ). Функция (219.3) представляет собой плоскую монохромати­ческую волну де Бройля (см. (217.2)).

Из выражения (219.2) следует, что зависимость энергии от импульса

оказывается обычной для нерелятивистских частиц. Следовательно, энергия свободной частицы может принимать любые значения (так как волновое число k может принимать любые положительные значения), т. е. ее энергетический спектр является непрерывным.

Таким образом, свободная квантовая частица описывается плоской монохроматической волной де Бройля. Этому соответствует не зависящая от времени плотность вероятности обнаружения частицы в данной точке пространства

т. е. все положения свободной частицы в пространстве являются равновероятными.

Частица в одномерной прямоугольной «потенциальной яме

Проведем качественный анализ решений уравнения Шредингера применительно к частице в одномерной прямоугольной «потенциальной яме» с бесконечно высокими «стенками». Такая «яма» описывается потенциальной энергией вида (для простоты принимаем, что частица движется вдоль оси х)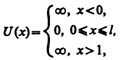

где l — ширина «ямы», а энергия отсчитывается от ее дна (рис. 296).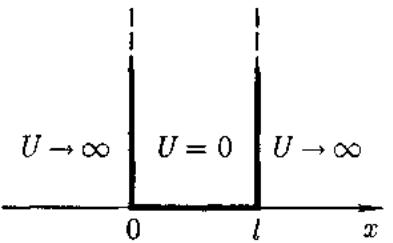

Уравнение Шредингера (217.5) для стационарных состояний в случае одномерной задачи запишется в виде                                      По условию задачи (бесконечно высокие «стенки»), частица не проникает за пределы «ямы», поэтому вероятность ее обнаружения (а следовательно, и волновая функция) за пределами «ямы» равна нулю. На границах «ямы» (при х=0 и х=1) непрерывная волновая функция также должна обращаться в нуль. Следовательно, граничные усло­вия в данном случае имеют вид пределах «ямы» (0 £ х £ l) уравнение Шредингера (220.1) сведется к уравнению или где   Общее решение дифференциального уравнения (220.3):

Так как по (220.2) y(0)=0, то В=0. Тогда  Условие (220.2) y(l)=A sin kl = 0 выполняется только при kl = np, где n — целые числа, т. е. необходимо, чтобы   Из выражений (220.4) и (220.6) следует, что   т. е. стационарное уравнение Шредингера, описывающее движение частицы в «потенциальной яме» с бесконечно высокими «стенками», удовлетворяется только при собственных значениях Е_n, зависящих от целого числа п. Следовательно, энергия Е_n частицы в «потенциальной яме» с бесконечно высокими «стенками» принимает лишь определенные дискретные значения, т.е. квантуется. Квантованные значения энергии Е_n называются уровнями энергии, а число п, определяющее энергетические уровни частицы, называется главным квантовым числом. Таким образом, микрочастица в «потенциальной яме» с бесконечно высокими «стенками» может находиться только на определенном энергетическом уровне Е_n, или, как говорят, частица находится в квантовом состоянии n.

Подставив в (220.5) значение k из (220.6), найдем собственные функции:

Постоянную интегрирования А найдем из условия нормировки (216.3), которое для данного случая запишется в виде В результате интегрирования получим А = , а собственные функции будут иметь вид Графики собственных функций (220.8), соответствующие уровням энергии (220.7) при n = 1, 2, 3, приведены на рис. 297,а. На рис. 297,6 изображена плотность вероятности обнаружения частицы на различных расстояниях от «стенок» ямы, равная |y_n(х)|² = y_n(х)y*_n(х) для n=1,2 и 3. Из рисунка следует, что, например, в квантовом состоянии с n=2 частица не может находиться в середине «ямы», в то время как одинаково часто может пребывать в ее левой и правой частях. Такое поведение частицы указывает на то, что представления о траекториях частицы в квантовой механике несостоятельны.

Из выражения (220.7) вытекает, что энергетический интервал между двумя сосед­ними уровнями равен  Например, для электрона при размерах ямы l=10^–1 м (свободные электроны в метал­ле) DE_n » 10^–35n Дж » 10^–16n эВ, т. е. энергетические уровни расположены столь тесно, что спектр практически можно считать непрерывным. Если же размеры ямы соизмеримы с атомными (l»10^–10 м), то для электрона DE_n » 10^–17n Дж » 10²n эВ, т. е. получаются явно дискретные значения энергии (линейчатый спектр). Таким образом, применение уравнения Шредингера к частице в «потенциальной яме» с бесконечно высокими «стенками» приводит к квантованным значениям энергии, в то время как классическая механика на энергию этой частицы никаких ограничений не накладывает.

Кроме того, квантово-механическое рассмотрение данной задачи приводит к выводу, что частица «в потенциальной яме» с бесконечно высокими «стенками» не может иметь энергию меньшую, чем минимальная энергия, равная . Наличие отличной от нуля минимальной энергии не случайно и вытекает из соотношения неопределенностей. Неопределенность координаты Dх частицы в «яме» шириной l рав­на Dx=l. Тогда, согласно соотношению неопределенностей (215.1), импульс не может иметь точное, в данном случае нулевое, значение. Неопределенность импульса Dp»h/l. Такому разбросу значений импульса соответствует кинетическая энергия E_min»(Dp)²/(2m) = h²/(2ml²). Все остальные уровни (n>1) имеют энергию, превыша­ющую это минимальное значение.

Из формул (220.9) и (220.7) следует, что при больших квантовых числах (n>>1) DE_n/E_n»2/n<<1, т. е. соседние уровни расположены тесно: тем теснее, чем больше n. Если n очень велико, то можно говорить о практически непрерывной последователь­ности уровней и характерная особенность квантовых процессов — дискретность — сглаживается. Этот результат является частным случаем принципа соответствия Бора (1923), согласно которому законы квантовой механики должны при больших значениях квантовых чисел переходить в законы классической физики.

Более общая трактовка принципа соответствия, имеющего огромную роль в современной физике, заключается в следующем: всякая новая, более общая теория, являющаяся развитием классической, не отвергает ее полностью, а включает в себя классическую теорию, указывая границы ее применения, причем в определенных предельных случаях новая теория переходит в старую. Так, формулы кинематики и динамики специальной теории относительности переходят при v<<с в формулы механики Ньютона. Например, хотя гипотеза де Бройля приписывает волновые свойства всем телам, но в тех случаях, когда мы имеем дело с макроскопическими телами, их волновыми свойствами можно пренебречь, т. е. применять классическую механику Ньютона.

Билет №19 1.Рассмотрим дифракцию в сходящихся лучах, или дифракцию Френеля, осуществляемую в том случае, когда дифракционная картина наблюдается на конечном расстоянии от препятствия, вызвавшего дифракцию.

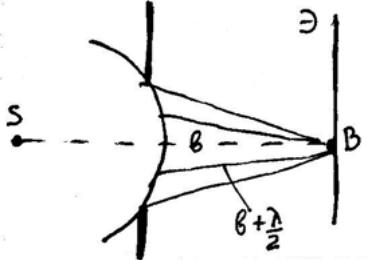
Дифракция на круглом отверстии. Сферическая волна, распространяющаяся из точечного источника S, встречает на своем пути экран с круглым отверстием. Дифракционную картину наблюдаем на экране Э в точке В, лежащей на линии, соединяющей S с центром отверстия (рис. 259). Экран параллелен плоскости отверстия и находится от него на расстоянии b. Разобьем открытую часть волновой поверхности Ф на зоны Френеля. Вид дифракционной картины зависит от числа зон Френеля, открываемых отверстием. Амплитуда результирующего колебания, возбуждаемого в точке В всеми зонами (см. (177.1) и (177.6)), где знак плюс соответствует нечетным m и минус — четным т.

Когда отверстие открывает нечетное число зон Френеля, то амплитуда (интенсив­ность) в точке В будет больше, чем при свободном распространении волны; если четное, то амплитуда (интенсивность) будет равна нулю. Если отверстие открывает одну зону Френеля, то в точке В амплитуда А=А₁, т. е. вдвое больше, чем в отсутствие непрозрачного экрана с отверстием. Интенсивность света больше соответственно в четыре раза. Если отверстие открывает две зоны Френеля, то их действия в точке В практически уничтожат друг друга из-за интерференции. Таким образом, дифракционная картина от круглого отверстия вблизи точки В будет иметь вид чередующихся темных и светлых колец с центрами в точке В (если т четное, то в центре будет темное кольцо, если m нечетное — то светлое кольцо), причем интенсивность в максимумах убывает с расстоянием от центра картины.

Расчет амплитуды результирующего колебания на внеосевых участках экрана более сложен, так как соответствующие им зоны Френеля частично перекрываются непроз­рачным экраном. Если отверстие освещается не монохроматическим, а белым светом, то кольца окрашены.

Число зон Френеля, открываемых отверстием, зависит от его диаметра. Если он большой, то А_m<<A₁ и результирующая амплитуда A=A₁/2, т. е. такая же, как и при полностью открытом волновом фронте. Никакой дифракционной картины не наблю­дается, свет распространяется, как и в отсутствие круглого отверстия, прямолинейно.

2. Дифракция на диске. Сферическая волна, распространяющаяся от точечного источника S, встречает на своем пути диск. Дифракционную картину наблюдаем на экране Э в точке В, лежащей на линии, соединяющей S с центром диска (рис. 260). В данном случае закрытый диском участок волнового фронта надо исключить из рассмотрения и зоны Френеля строить начиная с краев диска. Пусть диск закрывает m первых зон Френеля. Тогда амплитуда результирующего колебания в точке В равна

или так как выражения, стоящие в скобках, равны нулю. Следовательно, в точке В всегда наблюдается интерференционный максимум (светлое пятно), соответствующий поло­вине действия первой открытой зоны Френеля. Центральный максимум окружен концентрическими с ним темными и светлыми кольцами, а интенсивность в максимумах убывает с расстоянием от центра картины.

С увеличением радиуса диска первая открытая зона Френеля удаляется от точки В и увеличивается угол j_т (см. рис. 258) между нормалью к поверхности этой зоны и направлением на точку В. В результате интенсивность центрального максимума с увеличением размеров диска уменьшается. При больших размерах диска за ним наблюдается тень, вблизи границ которой имеет место весьма слабая дифракционная картина. В данном случае дифракцией света можно пренебречь и считать свет распространяющимся прямолинейно.

Отметим, что дифракция на круглом отверстии и дифракция на диске впервые рассмотрены Френелем.

2. Большую роль в выяснении строения атома, а именно распределения электронов по оболочкам, сыграло излучение, открытое в 1895 г. немецким физиком В. Рентгеном (1845—1923) и названное рентгеновским. Самым распространенным источником рент­геновского излучения является рентгеновская трубка, в которой сильно ускоренные электрическим полем электроны бомбардируют анод (металлическая мишень из тяже­лых металлов, например W или Pt), испытывая на нем резкое торможение. При этом возникает рентгеновское излучение, представляющее собой электромагнитные волны с длиной волны примерно 10^–12—10^–8 м. Волновая природа рентгеновского излучения доказана опытами по его дифракции.

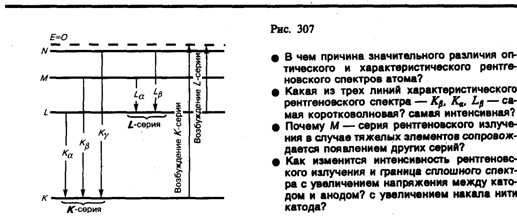
Исследование спектрального состава рентгеновского излучения показывает, что его спектр имеет сложную структуру (рис. 306) и зависит как от энергии электронов, так и от материала анода. Спектр представляет собой наложение сплошного спектра, ограниченного со стороны коротких длин волн некоторой границей l_min, называемой границей сплошного спектра, и линейчатого спектра — совокупности отдельных линий, появляющихся на фоне сплошного спектра.

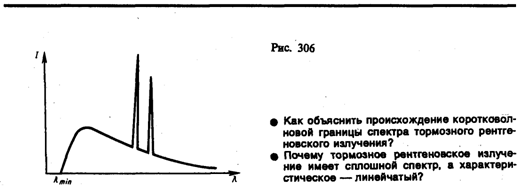
Исследования показали, что характер сплошного спектра совершенно не зависит от  материала анода, а определяется только энергией бомбардирующих анод электронов. Детальное исследование свойств этого излучения показало, что оно испускается бомбардирующими анод электронами в результате их торможения при взаимодействии с атомами мишени. Сплошной рентгеновский спектр поэтому называют тормозным спектром. Этот вывод находится в согласии с классической теорией излучения, так как при торможении движущихся зарядов должно действительно возникать излучение со сплошным спектром.

Из классической теории, однако, не вытекает существование коротковолновой границы сплошного спектра. Из опытов следует, что чем больше кинетическая энергия электронов, вызывающих тормозное рентгеновское излучение, тем меньше l_min. Это обстоятельство, а также наличие самой границы объясняются квантовой теорией. Очевидно, что предельная энергия кванта соответствует такому случаю торможения, при котором вся кинетическая энергия электрона переходит в энергию кванта, т. е. где U—разность потенциалов, за счет которой электрону сообщается энергия Е_max, n_max — частота, соответствующая границе сплошного спектра. Отсюда граничная дли­на волны что полностью соответствует экспериментальным данным. Измеряя границу рентгеновского сплошного спектра, по формуле (229.1) можно определить эксперименталь­ное значение постоянной Планка h, которое наиболее точно совпадает с современными данными.

При достаточно большой энергии бомбардирующих анод электронов на фоне сплошного спектра появляются отдельные резкие линии — линейчатый спектр, опреде­ляемый материалом анода и называемый характеристическим рентгеновским спектром (излучением).

По сравнению с оптическими спектрами характеристические рентгеновские спектры элементов совершенно однотипны и состоят из нескольких серий, обозначаемых К, L, М, и O. Каждая серия, в свою очередь, содержит небольшой набор отдельных линий, обозначаемых в порядке убывания длины волны индексами a, b, g,... (К_a, К_b, К_g,.... L_a, L_b, L_g, ...). При переходе от легких элементов к тяжелым структура характеристичес­кого спектра не изменяется, лишь весь спектр смещается в сторону коротких волн. Особенность этих спектров заключается в том, что атомы каждого химического элемента, независимо от того, находятся ли они в свободном состоянии или входят в химическое соединение, обладают определенным, присущим только данному элементу линейчатым спектром характеристического излучения. Так, если анод состоит из нескольких элементов, то и характеристическое рентгеновское излучение представляет собой наложение спектров этих элементов.

Рассмотрение структуры и особенностей характеристических рентгеновских спек­тров приводит к выводу, что их возникновение связано с процессами, происходящими во внутренних, застроенных электронных оболочках атомов, которые имеют сходное строение.

Разберем механизм возникновения рентгеновских серий, который схематически показан на рис. 307. Предположим, что под влиянием внешнего электрона или высокоэнергетического фотона вырывается один из двух электронов K-оболочки атома. Тогда на его место может перейти электрон с более удаленных от ядра оболочек L, M, N,.... Такие переходы сопровождаются испусканием рентгеновских квантов и возникновением спектральных линий К-серии: К_a (L®K), K_b (M®K), K_g (N®K) и т. д. Самой длинно­волновой линией К-серии является линия K_a. Частоты линий возрастают в ряду K_a ® K_b ® K_g, поскольку энергия, высвобождаемая при переходе электрона на K-оболочку с более удаленных оболочек, увеличивается. Наоборот, интенсивности линий в ряду K_a ® K_b ® K_g убывают, так как вероятность переходов электронов с L-оболочки на K-оболочку больше, чем с более удаленных оболочек М и N. К-серия сопровождается обязательно другими сериями, так как при испускании ее линий появляются вакансии в оболочках L, M,..., которые будут заполняться электронами, находящимися на более высоких уровнях.

Аналогично возникают и другие серии, наблюдаемые, впрочем, только для тяжелых элементов. Рассмотренные линии характеристического излучения могут иметь тонкую структуру, поскольку уровни, определяемые главным квантовым числом, расщепляются согласно значениям орбитального и магнитного квантовых чисел.

Исследуя рентгеновские спектры элементов, английский физик Г. Мозли (1887—1915) установил в 1913 г. соотношение, называемое законом Мозли:     где n — частота, соответствующая данной линии характеристического рентгеновского излучения, R — постоянная Ридберга, s — постоянная экранирования, т = 1, 2, 3, ... (определяет рентгеновскую серию), n принимает целочисленные значения начиная с m+1 (определяет отдельную линию соответствующей серии). Закон Мозли (229.2) подобен обобщенной формуле Бальмера (209.3) для атома водорода.

Смысл постоянной экранирования заключается в том, что на электрон, совершающий переход, соответствующий некоторой линии, действует не весь заряд ядра Zе, а заряд (Z–s)e, ослабленный экранирующим действием других электронов. Напри­мер, для K_a-линии s = 1, и закон Мозли запишется в виде