13.Определение потенциала

по заданному распределению зарядов в пространстве

Потенциал в поле точечного заряда определяется по выражению приведенному выше. Если поле создается системой “n” точечных зарядов, то

. (5.74)

Пусть заряд распределен по объему. В этом случае весь объем можно разбить на малые объемы с зарядами dq . Тогда

. (5.75)

Пусть задано распределение заряда в пространстве, т. е. известна плотность заряда в любой точке: ρ(x, y, z). Тогда dq = ρ dv и

. (5.76)

Если заряды распределены по поверхности с поверхностной плотностью σ, то

. (5.77)

14.Уравнение Пуассона и Лапласа

Рассмотрим теорему Гаусса (второе уравнение Максвелла):

. (5.78)

В развернутом виде имеем:

. (5.79)

В тоже время

; ; .

После подстановки получается уравнение Пуассона:

. (5.80)

Для тех точек поля, где нет зарядов, получается уравнение Лапласа:

.

Это уравнения в частных производных, имеющие бесчисленное множество решений. Единственное решение может быть найдено с учетом граничных условий.

Рис. 5.10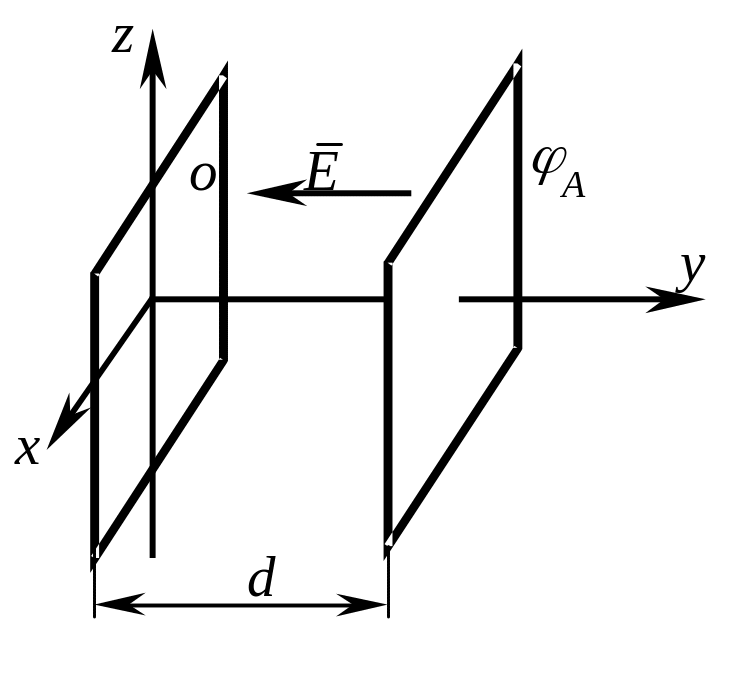

Пример: Пусть даны две бесконечно больших заряженные пластины с потенциалами 0 и _А (рис. 5.10)_. Ввиду бесконечности размеров поле между пластинами равномерное. Следовательно, производные по координатам x и z равны нулю. Тогда

;

d = C₁ dy;

 = C₁ y + C₂ .

Определим постоянные интегрирования с учетом граничных условий. При y = 0  = 0,

0 = С₁ 0 +С₂ , С₂ =0.

при y = d  = _А . Тогда: _А = С₁ d , C₁ = _A / d. Отсюда получаем окончательное выражение для потенциала между пластинами:

.

Напряженность между пластинами:

.

Напряженность постоянна и направлена в обратную сторону по отношению к оси y.

15.Г Рис. 5.11 раничные условия

Пусть заряд расположен на поверхности проводящего тела. В этом случае заряд распределяется по поверхности равномерно. Выделим бесконечно малый объем в виде цилиндра (рис. 5.11), с бесконечно малой высотой и ограниченный замкнутой поверхностью. К этой поверхности применим постулат Максвелла:

. (5.81)

Можно считать, что боковая поверхность равна нулю. Внутри проводящего тела поле отсутствует. Тогда весь поток будет идти только через внешнюю торцовую поверхность цилиндра. Суммарный заряд, находящийся внутри цилиндра равен поверхностной плотности заряда умноженной на поверхность ds. Так как в пределах торцовой поверхности вектор постоянен, то можно записать:

, (5.82)

т. е.

D = σ , и E = σ/ε_a .