1. Формула Бернулли

При решении вероятностных задач часто приходится сталкиваться с ситуациями, в которых одно и то же испытание повторяется многократно. Причем вероятность появления некоторого события А в каждом испытании не изменяется. Например, подбрасывают монету 5 раз. В каждом испытании герб может появиться с одной и той же вероятностью 1/2; стрелок стреляет по мишени 10 раз, при каждом выстреле вероятность попадания одна и та же. Такие ситуации носят название схемы повторных испытаний . Итак, опишем модель схемы повторных испытаний: проводятся п независимых испытаний, в каждом из которых событие А может наступить с одинаковой вероятностью и является случайным. Интерес представляет вопрос о вероятности появления события А в т из п проведенных испытаниях. Рассмотрим задачу: проводятся 5 независимых испытаний, в каждом из которых событие А может появится с одинаковой вероятностью р. вычислить вероятность того, что событие А появится в трех из проведенных пяти испытаниях.

Обозначим А_i - появление события А в i-том испытании, тогда А_i -не появление события А в i-том испытании. Рассмотрим все возможные случаи появления события А в двух случаях из пяти:

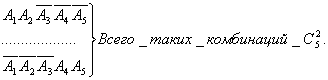Найдем вероятность для каждого исхода. Пользуясь теоремой умножения вероятностей для независимых событий. Заметим, что полученные вероятности будут равны, т.к. произведения отличаются только порядком множителей, тогда, применяя теорему сложения вероятностей для несовместных событий, получим выражение для вычисления вероятности события В- событие А появится в двух испытаниях из пяти проводимых: Обозначим 1-р=q, тогда Вероятность Р(В) обозначим _Р5(2) , т.е. вероятность появления события А в двух из пяти независимых испытаниях.

Обобщим результаты задачи и запишем формулу, позволяющую вычислить вероятность появления события А в т испытаниях из п проводимых: Полученная формула называется формулой Бернулли.

Если необходимо вычислить вероятность появления события А в диапазоне от т₁ до т₂ , то применяется теорема сложения вероятностей для независимых событий.

Проиллюстрируем применение формулы Бернулли. Пример1. Монету бросают 8 раз. Какова вероятность, что герб выпадет 4 раза? Решение:В каждом испытании герб может появиться с одинаковой вероятностью 1/2 и с такой же вероятностью- не появится. Тогда, применяя формулу, получим:

Билет 6

1. Дискретная случайная величина, закон и функция распределения

Дискретной называют случайную величину, значения которой изменяются не плавно, а скачками, т.е. могут принимать только некоторые заранее определённые значения. Например, денежный выигрыш в какой-нибудь лотерее, или количество очков при бросании игральной кости, или число появления события при нескольких испытаниях. Число возможных значений дискретной случайной величины может быть конечным или бесконечным (счётным множеством) Для сравнения - непрерывная случайная величина может принимать любые значения из некоторого числового промежутка: например, температура воздуха в определённый день, вес ребёнка в каком-либо возрасте, и т.д.

Закон распределения дискретной случайной величины представляет собой перечень всех её возможных значений и соответствующих вероятностей. Сумма всех вероятностей Σp_i = 1. Закон распределения также может быть задан аналитически (формулой) и графически (многоугольником распределения, соединяющим точки (x_i; p_i)

Функция распределения случайной величины - это вероятность того, что случайная величина (назовём её ξ) примет значение меньшее, чем конкретное числовое значение x: F(X) = P(ξ < X). Для дискретной случайной величины функция распределения вычисляется для каждого значения как сумма вероятностей, соответствующих всем предшествующим значениям случайной величины. Ниже будет приведён пример, разъясняющий смысл сказанного.

Билет 6,7