
- •В. Н. Степанов дискретная математика: графы и алгоритмы на графах
- •Предисловие
- •1. Основные понятия теории графов
- •1.1. Граф и его разновидности
- •1.2. Морфизмы графов
- •1.3. Степени вершин
- •1.4. Маршруты, цепи, циклы, связность
- •1.5. Операции над графами
- •1.6. Примеры графов
- •1.7. Метрические характеристики графов
- •1.8. Представления графов
- •2. Алгоритмы и сложность
- •2.1. Понятие алгоритма
- •2.2. Сложность алгоритма
- •2.3. Запись алгоритма
- •3. Обходы графов
- •3.1. Поиск в глубину на графе
- •3.2. Поиск в ширину на графе
- •3.3. Алгоритм выделения компонент связности
- •4. Деревья
- •4.1. Деревья. Свойства деревьев
- •4.2. Остовы. Теорема Кирхгофа
- •4.3. Теорема Кэли
- •4.4. Фундаментальная система циклов. Цикломатическое число
- •4.5. Алгоритм отыскания фундаментального множества циклов на графе
- •5. Остов минимального веса. Алгоритм Краскала и Прима
- •5.1. Алгоритм д. Краскала
- •5.2. Алгоритм р. Прима
- •6. Кратчайшие пути между вершинами графа
- •6.1. Алгоритм Дейкстры
- •6.2. Алгоритм Флойда
- •7. Эйлеровы графы
- •7.1. Теорема Эйлера
- •7.2. Алгоритм Флёри
- •8. Гамильтоновы графы
- •8.1. Гамильтоновы маршруты. Задача коммивояжера
- •8.2. Существование гамильтоновых маршрутов
- •9. Алгоритмы отыскания гамильтоновых циклов
- •9.1. Алгоритм с возвратом (полного перебора)
8.2. Существование гамильтоновых маршрутов
В этом пункте рассматриваются условия, гарантирующие существование гамильтоновых контуров и циклов.
Теорема 8.2.1. [Кёниг Д.]. В полном ориентированном графе (любая пара вершин которого соединена хотя бы в одном направлении) всегда существует гамильтонов путь.
Доказательство.
Пусть
![]() – путь длины
– путь длины
![]() ,
все вершины которого различны (длина
пути – это число дуг). Тогда, как нетрудно
показать (см. [3]), для любой вершины
,
все вершины которого различны (длина
пути – это число дуг). Тогда, как нетрудно
показать (см. [3]), для любой вершины
![]() ,
в силу полноты орграфа, можно построить
путь
,
в силу полноты орграфа, можно построить
путь
![]() ,
содержащий вершину
:
,
содержащий вершину
:
![]()
при
некотором
![]() .
Здесь
.
Здесь
![]()
![]()
Таким образом, можно шаг за шагом построить путь, содержащий все вершины графа по одному разу.
Теорема
8.2.2.
[Дирак Г., 1952 г.]. Если
в простом графе
порядка
![]() для любой вершины
выполняется неравенство
для любой вершины
выполняется неравенство
![]() ,
то граф
– гамильтонов.
,
то граф
– гамильтонов.
Доказательство.
От противного. Пусть
– не гамильтонов. Добавим
к графу
минимальное количество
новых вершин
![]() ,
соединяя каждую из них с каждой вершиной
графа
так, чтобы полученный граф
,
соединяя каждую из них с каждой вершиной
графа
так, чтобы полученный граф
![]() стал гамильтоновым. Затем, считая, что
,
придем
к противоречию.
стал гамильтоновым. Затем, считая, что
,
придем
к противоречию.
Пусть
![]() – гамильтонов цикл в графе
,
где
и
– гамильтонов цикл в графе
,
где
и
![]() – вершины из
,
а
– вершины из
,
а
![]() – одна из новых вершин. Такая пара вершин
и
– одна из новых вершин. Такая пара вершин
и
![]() в гамильтоновом цикле обязательно
найдется, иначе граф
был бы гамильтоновым. Тогда
в гамильтоновом цикле обязательно
найдется, иначе граф
был бы гамильтоновым. Тогда
![]() ,
иначе вершина
была бы не нужна. Более того, вершина
не является смежной с вершиной
,
иначе вершина
была бы не нужна.
,
иначе вершина
была бы не нужна. Более того, вершина
не является смежной с вершиной
,
иначе вершина
была бы не нужна.
Далее,
если в цикле
![]() есть вершина
есть вершина
![]() ,
смежная с вершиной
,
то вершина
,
смежная с вершиной
,
то вершина
![]() несмежна с вершиной
,
так как иначе можно было бы построить
гамильтонов цикл
несмежна с вершиной
,
так как иначе можно было бы построить
гамильтонов цикл
![]() без вершины
,
взяв последовательность вершин
без вершины
,
взяв последовательность вершин
![]() в обратном порядке. Из этого следует,
что число вершин графа
,
не являющихся смежными с
,
не меньше числа вершин, смежных с
(то есть больше либо равно
в обратном порядке. Из этого следует,
что число вершин графа
,
не являющихся смежными с
,
не меньше числа вершин, смежных с
(то есть больше либо равно
![]() ).
С другой стороны, очевидно, что число
вершин графа
,
смежных с
,
также больше либо равно
.
А так как ни одна вершина графа
не может быть одновременно смежной
и не смежной вершине
,
то общее число вершин графа
,
равное
).
С другой стороны, очевидно, что число
вершин графа
,
смежных с
,
также больше либо равно
.
А так как ни одна вершина графа
не может быть одновременно смежной
и не смежной вершине
,
то общее число вершин графа
,
равное
![]() ,
не меньше, чем
,
не меньше, чем
![]() .
Противоречие.
.
Противоречие.
Теорема
8.2.3.
[Оре О., 1960 г.]. Если
в графе
порядка
для любой пары несмежных вершин
и
выполняется неравенство
![]() то граф
– гамильтонов.
то граф
– гамильтонов.
Теорема Дирака является следствием теоремы Оре.
Теорема
8.2.4. [Хватал,
1972 г.] Пусть
G
– обыкновенный граф,
![]()
![]() –
его
степенная последовательность и
.
Если для любого k
верна импликация
–
его
степенная последовательность и
.
Если для любого k
верна импликация
![]() ,
,
то граф G – гамильтонов.
Пример 8.2.1. Покажем, что граф Петерсена (рис. 8.2.1) не гамильтонов.
В графе
Петерсена
![]() ,
,
![]() ,
поэтому
,
поэтому
![]() .
Следовательно, теорема Дирака не
выполняется. Теорема Оре также не
выполняется, так как
.
Следовательно, теорема Дирака не
выполняется. Теорема Оре также не
выполняется, так как
![]()
при
условии, что вершины
и
не смежны и
![]() .
.
Проверим
теперь условия теоремы Хватала. Для
![]() выясним истинность импликации
выясним истинность импликации
![]() .
.
Для
![]() – импликация истинна;
– импликация истинна;
Для
![]() – импликация истинна;
– импликация истинна;
Для
![]() – импликация не истинна;
– импликация не истинна;
Для
![]() – импликация не истинна.
– импликация не истинна.
Таким образом, для и условия теоремы нарушены и, следовательно, граф Петерсена не гамильтонов.
Известно, что почти нет эйлеровых графов (см. теорему 7.1.2). В противоположность к этому Перепелица доказал, что почти все графы гамильтоновы.
Теорема
8.2.5.
[Перепелица В.А., 1969 г.]. Пусть
– множество всех простых помеченных
графов с
вершинами,![]() – множество всех простых помеченных
гамильтоновых графов с
вершинами.
– множество всех простых помеченных
гамильтоновых графов с
вершинами.
Тогда
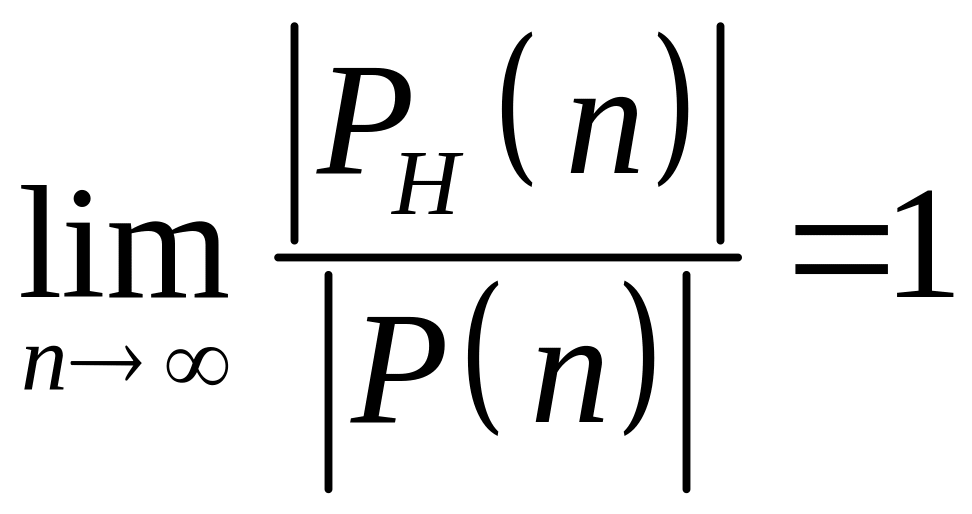 .
.
Таким образом, вероятность того, что «случайный граф» с вершинами является гамильтоновым, стремится с ростом к единице.

