9) Двойственные задачи. Двойственность в линейном программировании. Правила построения двойственных задач

Двойственная задача линейного программирования - формальная модель задачи линейного программирования, симметричная к исходной постановке в части управляемых переменных, коэффициентов целевой функции и ограничений.

Для ряда практических задач линейного программирования целесообразно заменить решение исходной прямой задачи решением соответствующей двойственной задачи, симметричной исходной. Для любой прямой задачи линейного программирования можно сформулировать двойственную задачу следующим образом.

Прямая задача: CX -> min при условиях AX >= B X >= 0

Двойственная задача: YB -> max при условиях YA =< C Y >= 0

В приведенной матричной формулировке симметричность обеих задач очевидна. При этом также очевидно, что задача двойственная к двойственной есть исходная прямая задача. Таким образом, из данной пары можно считать любую задачу прямой, а другую двойственной.

Из сравнения обеих задач видно, что:

1. Если в исходной задаче имеется n переменных и m ограничений, то в двойственной m переменных и n ограничений.

2. Матрица коэффициентов ограничений двойственной задачи получается транспонированием соответствующей матрицы прямой задачи.

3. В правых частях ограничений каждой задачи стоят коэффиценты целевой функции, взятой из другой задачи.

4. Знаки неравенств функциональных ограничений обеих задач являются взаимно-обратными.

5. Если в прямой задаче требуется минимизация целевой функции, то в двойственной задаче требуется максимизация целевой функции.

Правила построения пары двойственных задач

Рассмотрим пару задач ЛП вида:

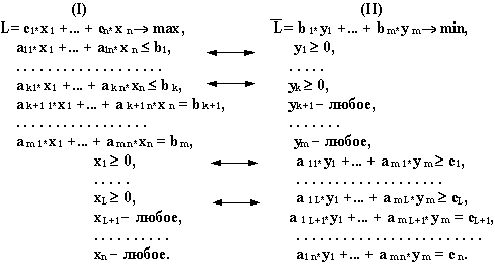
Задачу (I) называют прямой задачей ЛП, а (II) - двойственной. Ограничения задач (I) и (II), соответствующие друг другу (по стрелке), называются сопряженными. Заметим, что задача двойственная к (II), есть исходная прямая задача, т.е. соотношение двойственности взаимное. Поэтому можно любую из такой пары задач считать прямой, а другую двойственной.

Грубо говоря, двойственная задача - это на 90⁰ повернутая исходная прямая задача. В этой связи полезно усвоить следующую схему соответствия.

10) Три леммы о двойственных задачах. Первая теорема двойственности. Следствия.

Лемма 1. Если  и  - произвольные допустимые решения пары двойственных задач, то , если исходная задача на максимум, и , если она на минимум.

Доказательство. Дана симметричная пара двойственных задач:

исходная задача: найти максимум функции

                                                  ₍₄₎

при ограничениях:

 и                                       (5)

двойственная задача: найти минимум функции

                                                                                   ₍₆₎

при ограничениях:

                                                                         ₍₇₎

.

Пусть  - допустимое решение исходной задачи, т.е.  удовлетворяют неравенствам (5),  - допустимое решение двойственной задачи, т.е.  удовлетворяют неравенствам (7).

Тогда

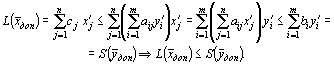
Аналогично рассматривается случай минимума.

Лемма 2. Достаточный признак оптимальности.

Если  и  - допустимые решения пары двойственных задач, для которых выполняется равенство , то  и  - оптимальные решения соответствующих задач.

Доказательство. Пусть  и  - допустимые решения пары двойственных задач, причем , и пусть исходная задача решается на максимум.

Возьмем произвольное допустимое решение исходной задачи , тогда по первой лемме . Получим т.е. , следовательно,  - оптимальное решение исходной задачи. Аналогично доказывается, что - оптимальное решение двойственной задачи.

Рассмотрим пару симметрических двойственных задач в матричной форме записи

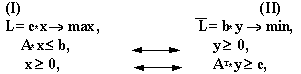
Здесь

А- матрица из m строк и n столбцов, - транспонированная матрица. Введем обозначения для допустимых областей задачи (I) и (II)

Первая теорема двойственности

Рассмотрим пару симметричных двойственных задач

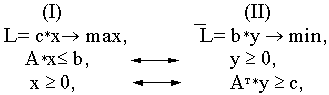
Первая теорема двойственности.

Если одна из пары двойственных задач (I) и (II разрешима, то разрешима и другая задача, причем оптимальные значения целевых функций прямой и двойственной задач совпадают

оптимальные планы задач (I) и (II) соответственно.

Доказательство.

1. Пусть задача (I) разрешима, и пусть

т.е. х* - оптимальное решение. Обозначим M= L(х*).

Тогда по основной лемме существует

для которого

Но по основному неравенству двойственности имеем :

Объединяя последние два соотношения, имеем 

откуда следует, что у* - оптимальное решение задачи (II) и

2. Пусть теперь задача (II) -разрешима. Построим эквивалентную (II) задачу

Задача (II') разрешима, так как задача (II) разрешима. Тогда по пункту 1 двойственная к (II') задача :

Но эта задача эквивалентна задаче (I). Следовательно, задача (I) разрешима.

Теорема доказана.

Первый критерий оптимальности

Решение оптимально тогда и только тогда, когда существует решение

  такое, что 

Доказательство.

Необходимость следует из первой теоремы двойственности.

Достаточность следует из достаточного условия оптимальности.

11) Вторая теорема двойственности. Анализ чувствительности решений. Теорема о маргинальных значениях. Симплекс-множители.

Рассмотрим пару симметрических двойственных задач ЛП

Вторая теорема двойственности

Чтобы допустимые решения х, у пары двойственных задач (I) и (II) были оптимальными необходимо и достаточно, чтобы выполнялись условия :

Доказательство.

Необходимость. По условию допустимые решения х, у - оптимальны.

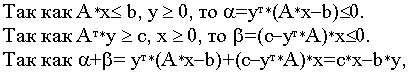
то из оптимальности решений х, у по первой теореме двойственности

В результате имеем 

Необходимость доказана.

Достаточность. По условию

По первой теореме двойственности получаем, что х, у - оптимальные решения задач (I) и (II).

Достаточность доказана.

Допустимые решения х, у задач (I) и (II) удовлетворяют условиям дополняющей нежесткости (УДН), если при подстановке этих векторов в ограничения задач (I) и (II) хотя бы одно из любой пары сопряженных неравенств обращается в равенство