5. Критерий доказательства вывода.

В результате освобождения строки Вонга от логических связок имеем

⊦ , т.е. строка Вонга имеет вид:

⊦ .

Если в левом списке и правом списке найдутся одинаковые переменные, то из P выводимо S (P ⊦.S).

На самом деле, по правилу 2) переноса переменной и «навешивания» на её знака отрицания.

Строка ⊦ 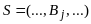и 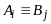, преобразованная по правилу 2) будет иметь вид

⊦ и далее при замене «,» на логическую связку «» в , где 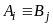получаем, что 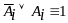и поэтому . Преобразовав строку Р⊦S в соответствующую импликацию PS и подставив S1, получим . Таким образом доказана выводимость S из Р.

Пример 5.

а) Постулируется выводимость 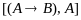⊦ (закон «modus ponens»).

Строка Вонга ⊦ .

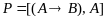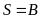по правилу 1) ⊦ преобразуется ⊦

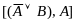по правилу 5) 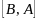⊦ содержит в левой и правой части одинаковые переменные. Выводимость доказана.

б) Постулируется выводимость ⊦ (закон «контрпозиции»).

по правилу 1) ⊦ .

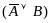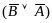по правилу 3) расщепление левой части строки 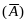⊦ и ⊦ .

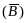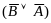по правилу 2) 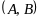⊦А и ⊦В

по правилу 5) Строки ⊦А и ⊦В в левых и правых частях содержат одинаковые переменные. Выводимость из 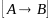доказана.

Проблемы аксиоматического исчисления высказываний

Всякая аксиоматическая теория для ее обоснования требует рассмотрения четырех проблем:

1. проблемы разрешимости,

2. проблемы непротиворечивости,

3. проблемы полноты,

4. проблемы независимости.

Проблема разрешимости исчисления высказываний.

Проблема разрешимости исчисления высказываний заключается в доказательстве существования алгоритма, который позволил бы для любой заданной формулы исчисления высказываний определить, является ли она доказуемой или не является.

Имеет место теорема: проблема разрешимости для исчисления высказываний разрешима.

Действительно, любая формула исчисления высказываний может рассматриваться как формула алгебры высказываний, и, следовательно, можно рассматривать ее логические значения на различных наборах значений входящих в нее переменных.

Пусть А – любая формула исчисления высказываний, а х₁,х₂,…,х_n – перечень входящих в нее переменных. Вычислим R_a1,a2,..,an(A) на всех наборах значений а₁, а₂,…,а_n входящих в нее переменных. Если при этом R_a1,a2,..,an(A)=1, на всех наборах а₁, а₂,…,а_n, то формула А – тождественно истинна, и, значит, по теореме о доказуемости тождественно истинной формулы она доказуема.

Если же существует набор значений переменных 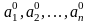такой, что , то формула А – не тождественно истинная, и, значит, по теореме 1 §8 она не доказуема.

2. Проблема непротиворечивости исчисления высказываний.

Логическое исчисление называется непротиворечивым, если в нем не доказуемы никакие две формулы, из которых одна является отрицанием другой.

Иначе говоря, аксиоматическое исчисление называется непротиворечивым, если в нем не существует такая формула А, что доказуема как формула А, так и формула .

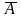Проблема непротиворечивости заключается в выяснении вопроса: является данное исчисление непротиворечивым или нет?

Если в исчислении обнаруживаются доказуемые формулы вида А и , то такое исчисление называется противоречивым. В рассмотренном нами исчислении высказываний невозможно вывести одновременно формулы А и , т.е. это исчисление высказываний непротиворечиво.