
- •1.Кольцо многочленов от переменных. Теорема 1. Теорема 2 (с док-вом). Примеры.
- •2.Лексикографическое упорядочение многочленов. Теорема (с док-вом). Примеры.
- •3.Смметрические многочлены. Основные симметрические многочлены. Теоремы 1. Теорема 2 (с док-вом).
- •4.Основная теорема о симметрических многочленах (с док-вом).
- •5.Следствие из основной теоремы о симметрических многочленах (с док-вом).
- •6.Степенная сумма. Применения основных симметрических многочленов от 2-х переменных.
- •7.Возвратные уравнения. Методы их решения.
- •8.Результант 2-х многочленов от одной переменной. Теорема 1 (с док-вом).
- •9.Резултант в форме Сильвестра. Теорема 2 (с док-вом)
- •10.Решение систем алгебраических уравнений с помощью результанта. Теорема (с док-вом).
- •12.Алгебраические и трансцендентные числа. Теорема о существовании неприводимого многочлена (с док-вом).
- •13.Теорема о комплексном числе, являющимся алгебраическим числом 1-й степени (с док-вом).
- •14.Теорема об изоморфизме фактор-кольцу (с док-вом).
- •15.Теорема об изоморфизме и (с док-вом).
- •16.Строение простого алгебраического расширения. Теорема об освобождении от иррациональности в знаменателе (с док-вом).
- •17.Теорема о представлении (с док-вом).
- •18.Теорема о как линейном n-мерном пространстве (с док-вом).
- •19.Теорема об алгебраическом расширении поля (с док-вом).
- •20.Строение простого трансцендентного расширения поля . Теорема (с док-вом).
- •21.Составное алгебраическое расширение поля . Теорема 1 (с док-вом).
- •22.Следствия 1 и 2 из теоремы о составном алгебраическом расширении поля (с док-вом).
- •23.Теорема о примитивном элементе (с док-вом).
- •24.Поле алгебраических чисел. Теорема 1 (с док-вом).
- •25.Теорема об алгебраической замкнутости поля алгебраических чисел (с док-вом).
- •26.Кольцо целых алгебраических чисел. Теорема (с док-вом).
- •27.Разрешимость алгебраических уравнений в квадратных радикалах.
- •28.Область рациональности. Теорема (с док-вом).
- •29.Разрешимость кубических уравнений в квадратных радикалах. Теорема (без док-ва), следствие.
- •30.Примеры задач, неразрешимых с помощью циркуля и линейки. Задача об удвоении куба.
- •31.Примеры задач, неразрешимых с помощью циркуля и линейки. Задача о трисекции угла.
12.Алгебраические и трансцендентные числа. Теорема о существовании неприводимого многочлена (с док-вом).
Рассмотрим
числовое поле
.
Опр.
Комплексное число α
назыв. алгебраическим относительно
поля
,
если в кольце многочленов
,
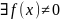 ,
т.ч.
явл. его корнем. Опр.
Комплексное
число
,
т.ч.
явл. его корнем. Опр.
Комплексное
число
 назыв. трансцендентным относительно
поля
,
если в кольце многочленов
,
назыв. трансцендентным относительно
поля
,
если в кольце многочленов
,
 ,
т.ч.
явл. его корнем. З!
Алгебр. (трансценд.) относительно поля
,
т.ч.
явл. его корнем. З!
Алгебр. (трансценд.) относительно поля
 назыв. просто алгебр. (просто трансценд.).
Если мы рассмотрим
,
то в кольце
назыв. просто алгебр. (просто трансценд.).
Если мы рассмотрим
,
то в кольце
 такие многочл., т.ч.
такие многочл., т.ч.
 явл. алгебр. Числа
явл. алгебр. Числа
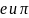 относит.
относит.
 явл. алгерб., т.к.
явл. алгерб., т.к.
 .
Т.
Если
алгеб.
число относительно поля
, то в
.
Т.
Если
алгеб.
число относительно поля
, то в
 не приводимый над полем
нормированный многочл.
не приводимый над полем
нормированный многочл.
 ,
т.ч.
явл. его корнем. Всякий многочл.
,
т.ч.
явл. его корнем. Всякий многочл.
 корнем которого явл число
корнем которого явл число
 .
(Доказательства
нет). Опр.
Нормиров. не приводимый над полем
многочл.
,
для которого алгебр. число α
явл. корнем назыв. мнимым многочл. алгебр.
числа α.
Опр.
Степенью min
многочл.
назыв. степенью алгебр. числа α
относительно поля
.
Опр.
Корни мнимого многочл.
для алгебр. числа α
назыв. числами сопряженные с α
относительно поля
.
.
(Доказательства
нет). Опр.
Нормиров. не приводимый над полем
многочл.
,
для которого алгебр. число α
явл. корнем назыв. мнимым многочл. алгебр.
числа α.
Опр.
Степенью min
многочл.
назыв. степенью алгебр. числа α
относительно поля
.
Опр.
Корни мнимого многочл.
для алгебр. числа α
назыв. числами сопряженные с α
относительно поля
.
13.Теорема о комплексном числе, являющимся алгебраическим числом 1-й степени (с док-вом).
Т.
Комплексное число α
явл. алгебр. числом первой степени
относительно поля
тогда и только тогда, когда α .
Док.:
Необх.:
Пусть α
- алгебр. число первой степени относительно
поля
следовательно
.
Док.:
Необх.:
Пусть α
- алгебр. число первой степени относительно
поля
следовательно
 неприводимый многочл.
неприводимый многочл.
 в кольце
,
т.к. его кофиц.
в кольце
,
т.к. его кофиц.
 полю
то и α
. Дост.:
Пусть α
,
тогда α
явл. многочл.
, который равен
полю
то и α
. Дост.:
Пусть α
,
тогда α
явл. многочл.
, который равен
 (неприводимый над полем
и нормированный в
с кофиц. из
)
(неприводимый над полем
и нормированный в
с кофиц. из
)
 следовательно
явл.
следовательно
явл.
 следовательно α
- алгебр. число первой степени относительно
поля
.
следовательно α
- алгебр. число первой степени относительно
поля
.
14.Теорема об изоморфизме фактор-кольцу (с док-вом).
Т.
Если
- алгебр. число
-й
степени относительно поля
 то
то
 изоморфно фактор кольцу кольца
по идеалу
изоморфно фактор кольцу кольца
по идеалу
 , где
- главный идеал порождающий
многочлен
для
.
Док.:
Если
, то
, где
- главный идеал порождающий
многочлен
для
.
Док.:
Если
, то
 определен однозначно, следовательно
определено отображение
определен однозначно, следовательно
определено отображение
 , такое что
, такое что
 , при этом , если
, при этом , если
 , и
, и
 ,
то образ
,
то образ
 или равен
или равен
 .
.
 .
Следовательно
.
Следовательно
 - гомоморфизм
- гомоморфизм
 .
Обозначим буквой
.
Обозначим буквой
 ,
т.е. это ядро гомоморфизма
.
Из теоремы 1 следует, что
,
т.е. это ядро гомоморфизма
.
Из теоремы 1 следует, что
 для которого алгебр. число
явл корнем
для которого алгебр. число
явл корнем
 на
многочл.
,
следовательно
на
многочл.
,
следовательно
 – множество порожд.
многочл.
,
т.е.
– есть главный идеал кольца
,
а по теореме гомоморфизма колец
– множество порожд.
многочл.
,
т.е.
– есть главный идеал кольца
,
а по теореме гомоморфизма колец
 .
.
15.Теорема об изоморфизме и (с док-вом).
Т.
Если
- трансцендентное число относительно
поля
,
то
 .
Док.:
Построим отображение
.
Док.:
Построим отображение
 ,
причем
,
причем
 надо доказать, что
- гомоморфизм
надо доказать, что
- гомоморфизм
 .
Докажем, что
- взаимно
однозначначный гомоморфизм. Предположим,
что
и
.
Докажем, что
- взаимно
однозначначный гомоморфизм. Предположим,
что
и
 .
Обозн.
.
Обозн. через
через
 и найдем образ
и найдем образ
 следовательно
следовательно
 ,
но это противоречит тому что
- трансцендентное число, следовательно
противоречие доказывает. что
взаимно однозначно, т.е.
– изоморфизм, следовательно
.
,
но это противоречит тому что
- трансцендентное число, следовательно
противоречие доказывает. что
взаимно однозначно, т.е.
– изоморфизм, следовательно
.
16.Строение простого алгебраического расширения. Теорема об освобождении от иррациональности в знаменателе (с док-вом).
 область
целосности, то
поле отношений, элементами которого
явл. дроби
область
целосности, то
поле отношений, элементами которого
явл. дроби
 .
Поле часных обозначается
.
Поле часных обозначается
 .
Опр.
Поле часности
.
Опр.
Поле часности
 назыв. простым расширением поля
получен. из поля
присоединением к полю числа
.
Опр.
Если элемент
явл. алгебр. (трансценд.) относителньо
поля
,
то
назыв. простым алгебр. (простым трансценд.)
расширением поля
.
Т.
Если примитивный элемент
явл. алгебр. числом
–й
степени относительно поля
,
то область целосности
совпадает с
.
Док.:
назыв. простым расширением поля
получен. из поля
присоединением к полю числа
.
Опр.
Если элемент
явл. алгебр. (трансценд.) относителньо
поля
,
то
назыв. простым алгебр. (простым трансценд.)
расширением поля
.
Т.
Если примитивный элемент
явл. алгебр. числом
–й
степени относительно поля
,
то область целосности
совпадает с
.
Док.:

 .
Покажем и обратное: возьмем
.
Покажем и обратное: возьмем
 элемент
элемент
 ,
,
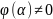 и покажем что этот элемент
области целосности
.
Т.к.
алгебр. число, следовательно ∃
мнимый многочл.
– неприводимый, корнем которого явл.
число
и покажем что этот элемент
области целосности
.
Т.к.
алгебр. число, следовательно ∃
мнимый многочл.
– неприводимый, корнем которого явл.
число
 ,
тогда по свойству неприводимого многочл.
,
тогда по свойству неприводимого многочл.
 или
или
 и
- взаимно простые.
не может делится на
,
т.к. мы бы имели
и
- взаимно простые.
не может делится на
,
т.к. мы бы имели
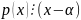 ,
следовательно
и
- корень
,
т.к.
, то по свойству НОДа ∃
его линейная форма
,
следовательно
и
- корень
,
т.к.
, то по свойству НОДа ∃
его линейная форма
 ,
перейдем и заменим x=
:
,
перейдем и заменим x=
:
 ,
,
 ,
,

