Министерство образования Республики Беларусь

Учреждение образования

«Гомельский государственный университет

имени Франциска Скорины»

Факультет математический

Кафедра теории функций и дифференциальных уравнений

Курс лекций

По предмету

Уравнения Математической Физики

Исполнители:

студенты группы М-31 ____________ Жук Д.А.

____________ Кашевич А.А.

____________ Крикало М.В.

____________ Тачилин Д.В.

Преподаватель: ____________ Вересович П.П.

Гомель 2011

Оглавление

1.Классификация уравнений в частных производных в точке (в области).

2.Приведение к каноническому виду линейных уравнений II-го порядка в случае 2-ух независимых переменных.

3. Приведение к каноническому виду линейных уравнений II-го порядка в случае n независимых переменных.

4.Постановка задачи Коши. Теорема Ковалевской.

5.Корректность постановки задачи. Пример Адамара.

6.Уравнение колебаний струны.

7.Уравнение малых продольных колебаний стержня.

8.Малые крутильные колебания вала.

9.Телеграфное уравнение. Частные случаи.

10.Уравнение колебаний мембраны.

11.Уравнение теплопроводности.

12.Задача Коши для одномерного волнового уравнения.

13.Осреднение функции на сфере и трехмерное волновое уравнение.

14.Задача Коши для трехмерного волнового уравнения. Формула Кирхгофа.

15.Задача Коши для волнового уравнения. Метод спуска. Формула Пуассона.

16.Единственность и устойчивость решения задачи Коши для волнового уравнения.

17.Элементарное (фундаментальное) решение уравнения теплопроводности.

18.Задача Коши для уравнения теплопроводности.

19.Принцип максимум-минимум для уравнения теплопроводности.

20.Единственность и устойчивость решения задачи Коши для уравнения теплопроводности.

21.Задача Штурма - Лиувилля. Свойства собственных значений и собственных функций.

22.Метод Фурье решения смешанных задач для однородных уравнений гиперболического и параболического типа.

23.Самосопряженность дифференциального оператора. Формулы Грина.

24.Смешанные задачи для неоднородных уравнений. Задачи с неоднородными граничными условиями.

25.Единственность решений смешанных задач для волнового уравнения и уравнения теплопроводности.

26.Свободные колебания прямоугольной мембраны.

27.Уравнение Бесселя. Функции Бесселя.

28.Радиальные колебания круглой мембраны.

29.Крутильные колебания вала с диском на конце.

30.Уравнение эллиптического типа.

31.Определение гармонической функции. Фундаментальное решение уравнения Лапласа.

32.Решение задачи Дирихле для уравнения Лапласа в круге и вне круга. Сходимость.

33.Внутренняя и внешняя задача Неймана для круга. Необходимое условие существования. Теорема Гаусса.

34.Метод Фурье решения задач Дирихле и Неймана для круговых областей ( в частности – для кольца).

35.Интегральное представление произвольной функции (гармонической).

36.Свойства гармонических функций : аналитичность и теорема о среднем на сфере.

37.Свойства гармонических функций: принцип максимума/минимума.

38.Единственность и устойчивость решения задачи Дирихле.

39.Функция Грина задачи Дирихле.

40.Функция Грина в задаче Неймана.

41.Формула Пуассона решения задачи Дирихле для шара.

42. Формула Пуассона решения задачи Дирихле для круга.

43.Неравенство Харнака. Теорема Лиувилля

44.Поведение производных гармонической функций на бесконечности.

45.Единственность решения задачи Неймана.

46.Потенциалы: объемный, простого слоя, двойного слоя.

47.Свойства объемного потенциала.

48.Свойства потенциала простого слоя.

49.Свойства потенциала двойного слоя.

50.Сведение краевых задач к интегральным уравнениям

1.Классификация уравнений в частных производных в точке (в области).

Будем изучать лин.ур-ния в частных производных 2-го порядка.

Любое ур-ние может быть записано в виде (1)

В (1) сделаем замену: ,при этом ,затем после подстановки в ур-ние (1) получим

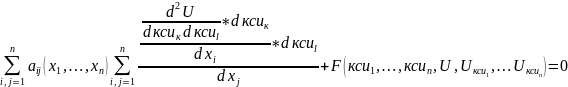
Если зафиксируем точку ( )то последнее ур-ние можно переписать в виде

-квадратичная форма.

Если ,а то

Рассмотрим квадратичную форму Q= и сделаем замену: Отсюда и получен способ классификации.

Из алгебры известно,что любая кВ.ю форма может быть приведена к виду: Q= ,где принимает значения 1,0 и -1.

Обозначим ч\з р число с -1,ч\з r число с 0 и ч\з & число с -1.Если р=n(&=n) a r=0,&=0(p=0) то ур-ние эллиптического типа, если p=n-1,&=1(или наоборот),r=0 то ур-ние гиперболического типа.Если р=n-1(&=n-1),r=1,&=0(p=0) то параболического типа.

Ур-ние типа наз ур-нием характеристик.

Рассм.ур-ние 2-го порядка в случае двух переменных: .Составим квадратичную формулу: Q=a(x,y) +2b(x,y)p(1)p(2)+c(x,y) =a[ +2 p(1)p(2)+ 2 - + ]=a[ ] .Обозначим δ=b*b-ac и назовем его дискриминантом. Если δ<0,то ур-ние эллиптического типа. Если δ=0 то параболического и если δ>0 то гиперболического типа.

2.Приведение к каноническому виду уравнения 2 – го порядка в случае

2 – х независимых переменных.

Рассмотрим уравнение . (1)

Выясним закон преобразования этого уравнения путем замены (2) при

После применения (2) мы перейдем к уравнению

(3)

Выразим производные по через производные по

Подставим найденные значения производных в уравнение (1) и выпишем коэффициенты при вторых производных по

(4)

Предположим, что уравнение (1) мы рассматриваем в области, где Уравнением характеристик для уравнения (1) будет уравнение

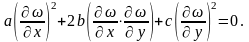
Положим в (4) - уравнение характеристик. Коэффициент в рассматриваемой области отличен от нуля, если же , то считаем, что

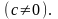
(5)

Пусть - общие интегралы последних двух уравнений.

В уравнении (1) сделаем замену

При выбранной замене переменных коэффициент =0. Так как коэффициент отличатся от только от искомой функции, то коэффициент =0Коэффициент в силу инвариантности типа уравнения отличен от нуля и разделив на удвоенные коэффициенты уравнение (3) мы получим канонический вид уравнения гиперболического типа.

Рассмотрим случай, когда - уравнение параболического типа. каноническому виду уравнения параболического типа

Рассмотрим теперь случай

Тогда уравнение характеристик примет вид:

канонический вид уравнения эллиптического типа

3.Приведение к каноническому виду уравнений второго порядка с постоянными коэффициентами в случае независимых переменных.

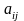Рассмотрим уравнение второго порядка (1), в котором коэффициенты - постоянны. Соответствующая этому уравнению квадратичная форма имеет вид: Эта квадратичная форма с помощью замены переменных при соответствующем выборе не особой матрицы приводится к каноническому виду ,

Уравнение (1) с помощью замены может быть приведено к виду

Установим связь между матрицами и . Для простоты рассуждения рассмотрим уравнение с двумя переменными.

(2), в котором коэффициенты постоянные, соответствующая этому уравнению квадратичная форма

Сделаем замену

В уравнении (1) сделаем замену: тогда

То есть,