- •Ответы на экзамен по курсу тВиМс.
- •1. Теория вероятностей
- •Биномиальный закон распределения
- •Центральная предельная теорема
- •2. Статистическое оценивание
- •3. Статистическая проверка гипотез
- •Мощность критерия при проверке гипотезы о значении генеральной средней
- •1. Критерий Бартлетта
- •2. Критерий Кохрена
- •Критерий Пирсона
Биномиальный закон распределения
Биноминальное
распределение представляет собой
распределение вероятностей возможных
чисел появления события А при n независимых
испытаний, в каждом из которых событие
А может осуществиться с одной и той же
вероятностью P(A)
= p
= const.
Кроме события A может произойти также
противоположное событие
![]() ,
вероятность которого P(
)
= 1-p = q.
,
вероятность которого P(
)
= 1-p = q.
Вероятности любого числа событий соответствуют членам разложения бинома Ньютона в степени, равной числу испытаний:
![]()
где
![]() -
вероятность того, что при n испытаниях
событие A наступит n раз;
-
вероятность того, что при n испытаниях
событие A наступит n раз;
![]() -
вероятность того, что при n испытаниях
событие A не наступит ни разу;
-
вероятность того, что при n испытаниях
событие A не наступит ни разу;
![]() -
вероятность того, что при n испытаниях
событие A наступит m раз, а событие
наступит n-m раз;
-
вероятность того, что при n испытаниях
событие A наступит m раз, а событие
наступит n-m раз;
![]() -
число сочетаний (комбинаций) появления
события A и
.
-
число сочетаний (комбинаций) появления
события A и
.
Таким образом, вероятность осуществления события A m раз при n независимых испытаниях с одинаковой вероятностью p можно рассчитать по формуле общего члена разложения бинома Ньютона:
![]() .
.
Эта формула называется формулой Бернулли. Ее целесообразно использовать при небольшом числе испытаний, порядка n 8.
Сумма вероятностей всех комбинаций равна единице,
![]()
как сумма вероятностей единственно возможных и несовместных событий (комбинаций), составляющих полную группу событий.
Ряд распределения вероятностей случайной величины X = m записывают следующим образом:
![]() ,
,
где n - число независимых испытаний;
m=0n - частота появления события A в n независимых испытаниях.
Числовые характеристики биноминального распределения:
M(m)=np - математическое ожидание частоты появлений события A при n независимых испытаниях;
D(m)=npq - дисперсия частоты появления события A;
![]() -
среднее квадратическое отклонение
частоты.
-
среднее квадратическое отклонение
частоты.
Когда число испытаний n велико, то для вычисления вероятности комбинаций используется локальная теорема Лапласа:
![]()
где
![]() -
нормированная плотность нормального
распределения;
-
нормированная плотность нормального
распределения;
![]() -
нормированное значение частоты.
-
нормированное значение частоты.
1.8
Нормальное распределение - наиболее часто встречающийся вид распределения. С ним приходится сталкиваться при анализе погрешностей измерений, контроле технологических процессов и режимов, а также при анализе и прогнозировании различных явлений в в экономике, социологии, демографии и других областях знаний.Нормальным называется распределение, функция плотности вероятности которого имеет вид
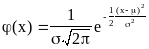 ,
,
где - математическое ожидание случайной величины;
2 - дисперсия случайной величины, характеристика рассеяния значений случайной величины около математического ожидания.
1.9
Правило 3-х _ (трех “сигм”).Пусть имеется нормально распределённая случайная величина с
математическим ожиданием, равным а и дисперсией 2. Определим вероятность попадания в интервал (а – 3_; а + 3_), то есть вероятность того, что принимает значения, отличающиеся от математического ожидания не более, чем на три среднеквадратических отклонения.
P(а – 3_< _ < а + 3_)=Ф(3) – Ф(–3)=2Ф(3)
По таблице находим Ф(3)=0,49865, откуда следует, что 2Ф(3) практически равняется единице. Таким образом, можно сделать важный вывод: нормальная случайная величина принимает значения, отклоняющиеся от ее математического ожидания не более чем на 3. (Выбор числа 3 здесь условен и никак не обосновывается: можно было выбрать 2,8, 2,9 или 3,2 и получить тот же вероятностный результат. Учитывая, что Ф(2)=0,477, можно было бы говорить и о правиле 2–х “сигм”.)
1.10
Схема испытаний Бернулли.
n испытаний
называются системой испытаний Бернулли,
если испытания независимы, в каждом из
них происходит событие
![]() ,
либо
,
либо
![]() с вероятностью наступления P(A) = p;
с вероятностью наступления P(A) = p;
![]()
Найдем вероятность
того, что в результате проведенных n
испытаний событие А произошло m раз:![]()
Рассмотрим композицию n независимых испытаний и построим композиционное пространство элементарных событий.
Общий вид элемента
этого пространства следующий:
![]()
где |
|
При этом вероятность
наступления такого события равна:
![]() (умножение
при независимых событиях)
(умножение
при независимых событиях)![]()
Найдем вероятность
наступления любого элементарного
события из композиционного пространства:
![]()
Рассмотрим в композиционном вероятностном пространстве событие: в n испытаниях событие A произошло m раз.
Событие A состоит
из
![]() - общее кол-во элементарных событий, в
которое входит событие А. А произошло
m раз,
- общее кол-во элементарных событий, в
которое входит событие А. А произошло
m раз,
![]() - n-m раз. Вероятность каждого из этих
элементарных событий одинакова и равна:
- n-m раз. Вероятность каждого из этих
элементарных событий одинакова и равна:![]()
Следовательно, на
основании III аксиомы теории вероятности
результат равняется:
![]() (сложение вероятностей)
(сложение вероятностей)
![]()
Локальная и интегральная теорема Лапласа
Пусть производится n одинаковых независимых испытаний с вероятностью появления события в каждом испытании, равной p. Тогда вероятность частоты m наступления события А определяется, как было показано ранее по формуле Бернулли:
![]()
Вычисление по этой формуле трудно практически осуществить при n>20.Муавром и Лапласом была получена асимптотическая формула, позволяющая найти указанную вероятность. Теорема, выражающая эту формулу, носит название локальной теоремы Муавра-Лапласа .Если производится n одинаковых испытаний, в каждом из которых вероятность появления события равна p, то вероятность того, что данное событие появится m раз, определяется по формуле
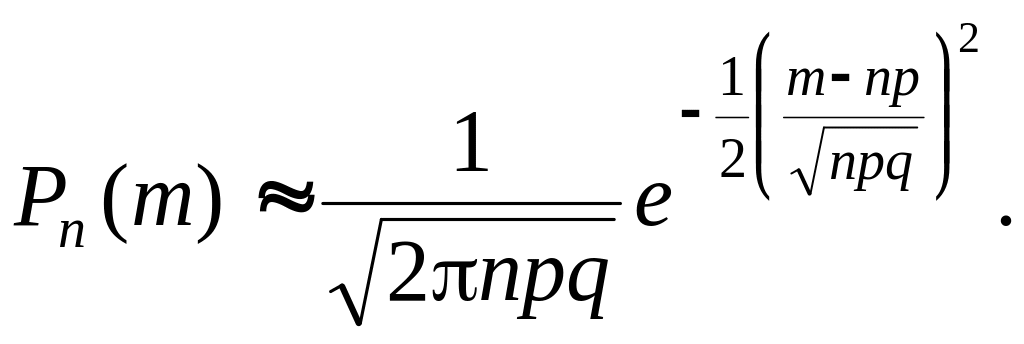
Эта теорема дает приближение биномиального закона распределения к нормальному при n и p, значительно отличающемся от нуля и единицы. Для практических расчетов удобнее представлять полученную формулу в виде
![]() ,
,
![]() ;
;
![]() .
.
Если m=m0=np,
то вероятность наиболее вероятной
частоты находится по формуле![]()
При рассмотрении количества m появлений события A в n испытаниях Бернулли чаще всего нужно найти вероятность того, что m заключено между некоторыми значениями a и b. При достаточно больших n промежуток [a,b] содержит большое число единиц, то непосредственное использование биномиального распределения:
![]()
требует громоздких
вычислений, так как нужно суммировать
большое число определённых по этой
формуле вероятностей. Поэтому используют
асимптотическое выражение для
биномиального распределения при условии,
что p
фиксированно, а
![]() .
Теорема Муавра-Лапласа утверждает, что
таким асимптотическим выражением для
биномиального распределения является
нормальная функция.
.
Теорема Муавра-Лапласа утверждает, что
таким асимптотическим выражением для
биномиального распределения является
нормальная функция.
Формулу, выражающую интегральную терему Лапласа, можно получить из закона нормального распределения (см. далее), положив
X
= m;
x1=m1;
x2=m2;
= np;
![]() При
больших значениях n наиболее вероятная
частота m0
совпадает с математическим ожиданием
(см. далее) частоты. Поэтому для нахождения
вероятности того, что абсолютная величина
отклонения частоты от наиболее вероятной
частоты не превосходит заданного числа
> 0, применим формулу закона нормального
распределения
При
больших значениях n наиболее вероятная
частота m0
совпадает с математическим ожиданием
(см. далее) частоты. Поэтому для нахождения
вероятности того, что абсолютная величина
отклонения частоты от наиболее вероятной
частоты не превосходит заданного числа
> 0, применим формулу закона нормального
распределения
P(X-<t) = Ф(t),
где X = m;
= M(m) = m0;
![]() ;
t
= .
;
t
= .
Заметим, что,
пользуясь теоремами Лапласа, можно
находить вероятность того, что частость
![]() примет заданное значение.
примет заданное значение.
1.11
Лемма Маркова
Пусть Х - случайная величина, принимающая лишь неотрицательные значения. Тогда можно получить следующее неравенство:
![]() (>0
любое)
(>0
любое)
Неравенство Чебышева.
Вероятность того,
что отклонение случайной величины Х от
ее математического ожидания по обсолютной
величине меньше положительного числа
,
не меньше, чем
![]() ,
то есть
,
то есть
![]()
Теорема Чебышева. Если Х1, Х2, … Хn попарно независемые случайные величины, причем дисперсии их не привышают постоянноо числа с, то как бы мало ни было положительное число , вероятность неравенства
![]()
будет как угодно близка к единице, если число n случайных величин достаточно велико.
Используя понятие предела, можно в условиях теоремы записать:
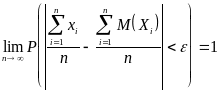 .
.
Вместо последней
записи часто кратко говорят, что суммы
![]() сходятся по вероятности к нулю.
сходятся по вероятности к нулю.
Теорема Бернулли. Пусть производится n независимых испытаний, в каждом из которых вероятность появления события постоянна и равна р. Тогда каково бы ни было >0,
![]() ,
,
где
![]() - частость появления события А.
- частость появления события А.
Теорема Пуассона. Если в последовательности независимых испытаний появление события А в К-ом испытании равна рк, то
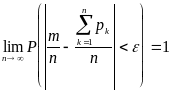 ,
,
где m есть случайная величина, равная числу появлений событя А в первых n испытаниях.
Теорема Лапласа.
Теоремы Чебышева, Бернулли, Пуассона устанавливают нижнюю границу вероятности, что часто бывает недостаточно. В некоторых случаях важно знать достаточно точное значение вероятности. Этому требованию отвечают так называемые предельные теоремы закона больших чисел, указывающие асимптотические формулы для
вероятностей
неравенства
![]() относительно n случайных величин Xi.
относительно n случайных величин Xi.
Мы уже знаем, что
вероятность неравенства
![]() вычисляется по интегральной теорема
Лапласа, а именно
вычисляется по интегральной теорема
Лапласа, а именно
![]() где
где
![]() .
.
Следовательно, достаточно точным выражением теоремы Бернулли является интегральная теорема Лапласа. Асимптотическую формулу для теоремы Чебышева доказал его ученик А.М. Ляпунов. Приведем теорему Ляпунова без доказательства.