2.15. Закон внутреннего трения (Закон Ньютона-Петрова)

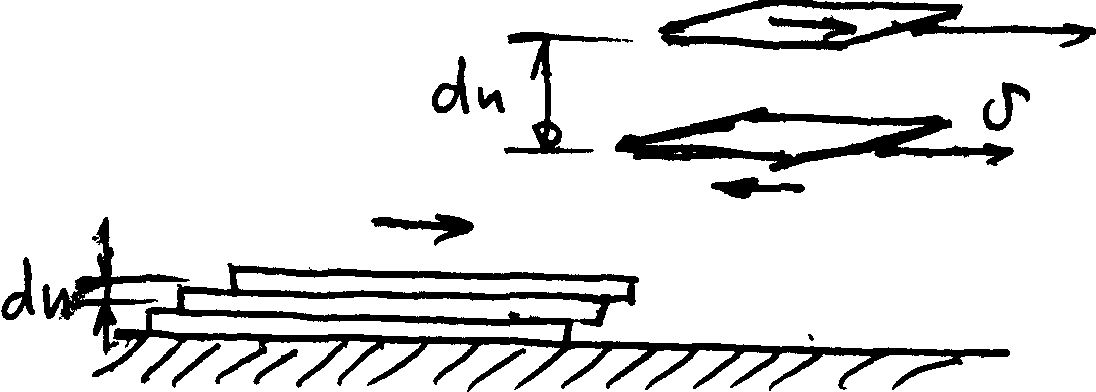В жидкости при наличии пере­мещения возникнут, и будут су­ществовать касательные напря­жения между соседними движу­щимися слоями. Ньютон предпо­ложил, что касательная сила (сила трения) может быть определена по следующей формуле:

где F - площадь соприкосновения сдоев, градиент скорости, который показывает, как быстро меняется скорость в направлении перпендикуляр­ном перемещению. Сила Т действует в направлении противоположном перемещению. Напряжение от силы трения будет равно:

Соотношение ( ) и является математическим выражением закона внутреннего трения. Напряжение внутреннего трения, возникающее меж­ду слоями жидкости при ее перемещении прямо пропорционально градиенту скорости. При движении жидкости происходит перенос количества движения в направлении перпендикулярном перемещению жидкости. Касательное напряжение можно рассматривать как удельный поток импульса, или количества движения, передаваемый через единицу поверхности в единицу времени:

Таким образом, удельный поток импульса прямо пропорционален градиен­ту скорости.

2.16. Жидкости поведение которых подчиняется закону Ньютона называют - нормальными или Ньютоновскими. Однако в промышленности приходится иметь дело и с неньютоновскими жидкостями, т.е. жидкостями обладающими аномальными свойствами. Не подчиняются закону Ньютона растворы многих полимеров, коллоидные растворы, густые суспензии, резиновые смеси, пасты и др. Одной из разновидностей неньютоновских жидкостей являются бингамовские жидкости. Поведение их при сдвиговых нагрузках описывается уравнением:

Для описания поведения большой группы жидкостей используется уравне­ние Оствальда-де Билля:

где K, m - константы, характеризующие течение жидкости. Если m<0, жидкости называются псевдопластическими, при m>0 дилатантными. Константы K, m определяется экспериментально, путем интерпретации кривых течения в логарифмических координатах:

2.17. Уравнение неразрывности

Это уравнение устанавливает зависимость между скоростями в пото­ке жидкости, для которого соблюдается условие сплошности или неразрывности течения. Выделим в пространстве прямоугольный параллелепи­пед с гранями размером вдоль осей координат соответственно dx, dy, dz. Грани параллельны соответствующим осям. Составляющие скорости потока вдоль υx, υy, υz. Составим уравнение материаль­ного баланса для выделенного элементарного объема.

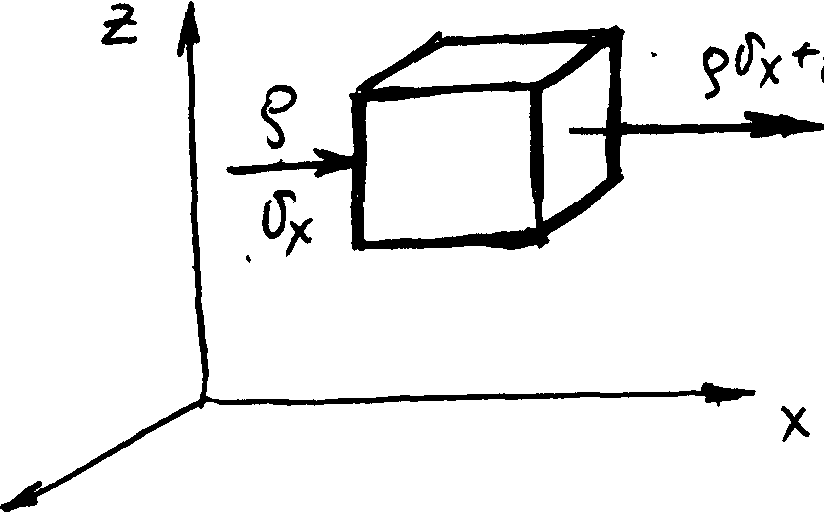
(Скорость накопления массы в элементарном объёме) = (Скорость подвода в элементарный объём) + (Скорость отвода из элементарного объёма)

Определим математически все составляющие уравнения ( ). Скорость накопления массы в элементарном объеме

Скорость подвода

Скорость отвода:

После подстановки значений скоростей в уравнение ( ) и преобразований, получим:

Если плотность по всем направлениям одинакова, т.е. жидкость не сжимаема, то уравнение примет вид:

Для стационарного режима будем иметь:

и

Для одномерного движения жидкости (наиболее часто встречающееся на практике) интегрирование уравнения ( ) дает: (при постоянном живом сечении потока)

Если сечение потока переменно по его длине, то будем иметь:

2.18.

Это уравнение неразрывности в интегральной форме.

2.19. Дифференциальные уравнения движения вязкой жидкости Уравнения Навье-Стокса.

Рассмотрим движение вязкой (Ньютоновской) жидкости в поле дейст­вия сил тяжести. При движении в потоке жидкости действуют силы тяжес­ти, давления и трения. Выделим в пространстве прямоугольный паралле­лепипед с гранями dx, dy, dz и соорентируем эти грани параллель­но соответствующим координатным осям. Оси выберем таким образом, чтобы сила тяжести была направлена вдоль оси к плоскости уох. Рассмотрим равновесие выделенного элемента под

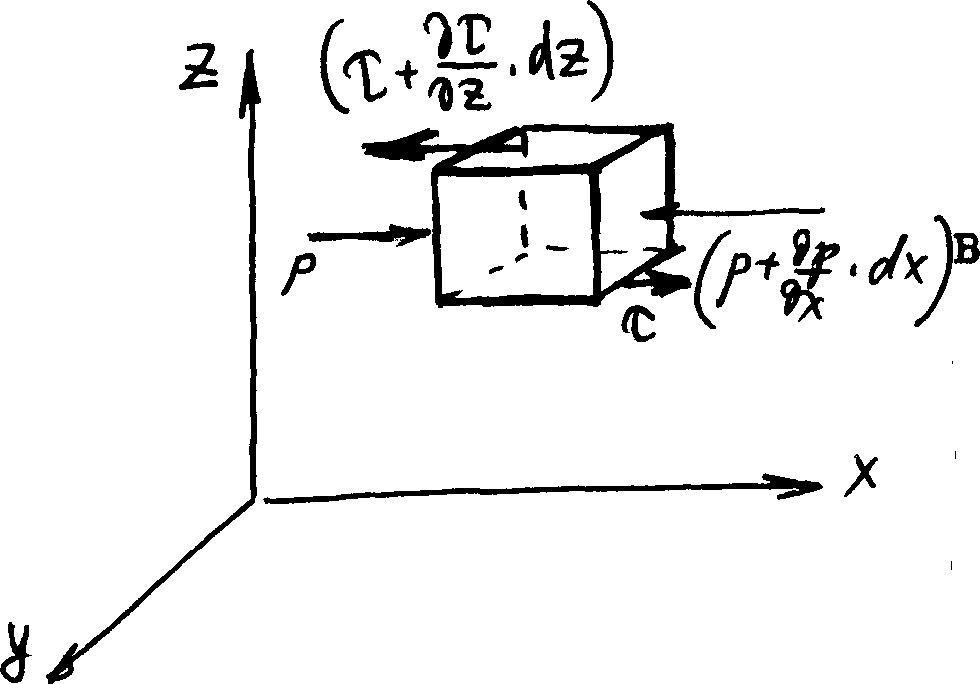
действием указанных сил. В соответствии с законом сохранения импульса из­менение количества движения в этом элементе будет равно сумме всех сил действующих на данный элемент:

(Изменение количества движения в элементарном объёме)

(Сумма сил, действующих на элемент)

Рассмотрим равновесие элемента в направлении оси X, а по осталь­ным осям запишем уравнения по аналогии. Равнодействующая от сил тре­ния будет равна

Но закону трения Ньютона-Петрова:

Тогда после подстановки

В общей случае составляющая скорости изменяется по всем направле­ниям и проекция составляющей силы трения на ось Х будет равна:

Равнодействующая сил давления будет равна:

По принципу Д’Аламбера сумма всех сил действующих вдоль оси на выделенный элемент равна произведению его массы на ускорение:

Подставляем значения всех слагаемых в уравнение ( ) и получим математическое выражение, определяющее равновесие элемента вдоль оси X:

Аналогично рассуждая можно получить уравнения для осей У и Z, при этом необходимо помнить, что вдоль оси Z действует сила тя­жести:

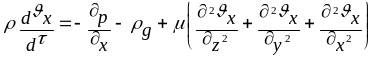
Полученная система уравнений носит название уравнений Навье-Стокса. Решение данной системы уравнений совместно с уравнением неразрыв­ности позволяет определить скорость движения точки в любой точке пространства и в любой момент времени. Аналитическое решение можно получить только для ряда конкретных примеров (течение в круглой трубе, течение по наклонной плоскости и т. д.) когда удается зна­чительно упростить исходные уравнения. Производная скорости в ле­вой части уравнений имеет сложный вид:

В зависимости от геометрии движущегося потока система уравнений может быть представлена в удобной системе координат.

2.21. Уравнения гидростатики Эйлера.

В состоянии покоя скорость жидкости равна нулю и все члены уравнений Навье-Стокса содержащие производные скорости тоже равны нулю и система уравнений понимает вид:

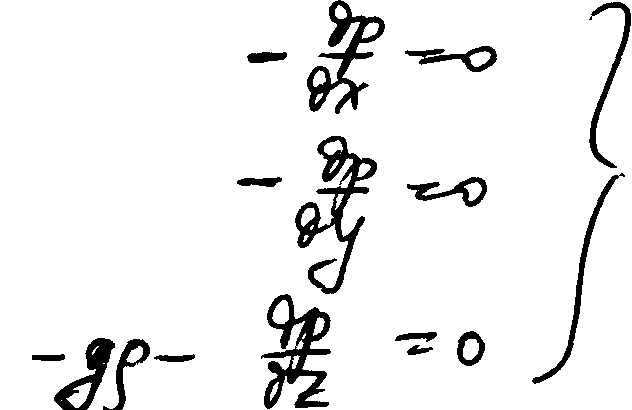
Полученная система уравнений носит название диффернциальных уравне­ний равновесия Эйлера. Данную систему уравнений можно интегрировать. Для этого каждое уравнение системы умножим соответственно на dx, dy, dz и сложим:

2.22.

После деления на dz получаем:

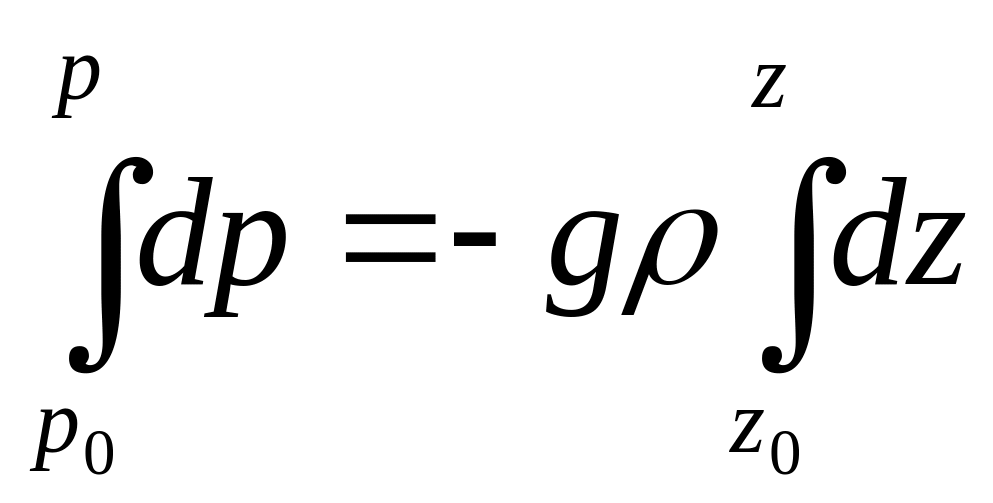
Интегрирование полученного уравнения дает:

Данное уравнение носит название основного уравнения гидростатики. Давление, создаваемое в любой точке покоящейся жидкости, передается всем точкам ее объема одинаково. При изменении P₂ на какую либо величину, давление P изменится на такую же величину.

Давление жидкости на плоскую наклонную стенку.

Необходимо определить силу давления по­коящейся жидкости на наклонную плоскую стенку, угол наклона которой к горизон­ту равен . Так как величина давления переменна, определим силу давления на элементарную площадку dF в пределах

которой давление можно считать постоянным:

Проинтегрируем это уравнение:

где , координата центра тя­жести площадки dF. Из механики извест­но, что интеграл в правой части представляет статический момент пло­щади F относительно оси X и равен произведению этой площади на ко­ординату ее центра тяжести y_c .Следовательно сила давления равна:

Таким образом, сила давления жидкости на плоскую стенку равна произве­дению площади стенки на величину гидростатического давления в центре тяжести этой площади.