3. Анализ систем управления

3.1. Задачи анализа

Анализ систем управления состоит в изучении их общесистемных свойств, условий выполнения ими своих функций и достижения заданных целей. В результате анализа качественно констатируются свойства поведения систем в целом и количественно оценивается степень удовлетворения требований к процессам управления. Анализ в широком смысле должен также объяснять, почему система с определенной структурой причинно-следственных взаимосвязей элементов с известными характеристиками имеет то или иное поведение.

Безусловными требованиями к свойствам поведения систем управления являются:

— устойчивость движений;

— инвариантность управляемой переменной к возмущениям и ковариантность с задающим воздействием;

— грубость (параметрическая инвариантность, робастность), т.е. ограниченная чувствительность свойств системы к вариациям характеристик элементов.

Основными задачами анализа систем управления, обычно решаемыми методами теории управления, являются:

— установление фактов устойчивости, инвариантности и робастности;

— построение характеристик и вычисление показателей качества;

— вывод об удовлетворительном (или неудовлетворительном) поведении системы.

3.2. Анализ устойчивости

Устойчивость по начальным условиям (по Ляпунову) — свойство собственно системы. Если система устойчива, то затухают все составляющие свободных движений, вызванных любыми ненулевыми начальными условиями. Свойство устойчивости линейных непрерывных систем анализируется по моделям типа (см. рис. 1.18) в форме однородных дифференциальных уравнений n-го порядка

(3.1)

или систем дифференциальных уравнений в форме пространства состояний

.

3.2.1. Свободные движения

Преобразуя дифференциальное уравнение (3.1) по Лапласу с учетом начальных условий: , получим

,

(3.2)

где  — полином, коэффициенты которого зависят от начальных условий. Из алгебраического уравнения (3.2) легко получить изображение решения уравнения (3.1)

.

В том случае, когда характеристический полином системы имеет только простые корни: , выражение для свободных движений имеет вид

.

(3.3)

Здесь знак () в выражении (3.3) означает дифференцирование полинома по s. Если корни полинома кратные, то вместо коэффициентов в выражении (3.3) появятся полиномы от t со степенями ниже кратности корня .

3.2.2. Условие устойчивости

Как следует из выражения (3.3), необходимым и достаточным условием затухания экспонент является отрицательность действительных частей корней

.

(3.4)

На рис. 3.1 изображен пример расположения корней характеристического полинома асимптотически устойчивой системы пятого порядка на комплексной плоскости. Все корни находятся в открытой левой полуплоскости, т.е. строго левее мнимой оси. Поэтому часто говорят, что для асимптотической устойчивости системы необходимо и достаточно, чтобы все корни характеристического полинома были левыми. Это же условие справедливо и для собственных значений матрицы состояний A.

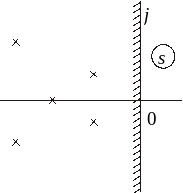Рис. 3.1. Пример расположения корней устойчивой системы

Заметим, что если характеристический полином имеет простые корни на мнимой оси, то имеет место устойчивость по Ляпунову (но не асимптотическая).

Вынужденные движения неавтономных линейных систем представляются как сумма установившихся движений, определяемых полюсами изображений воздействий и переходных процессов из-за посленулевых начальных условий, вызванных внезапным приложением воздействий. Если системы асимптотически устойчивы, то с течением времени процессы стремятся к установившимся

.