
- •3 Общее уравнение прямой.
- •4. Линии второго порядка
- •4.Эллипс и его каноническое уравнение
- •5.Гипербола
- •6.Парабола
- •7,8,9Понятие матрицы. Линейные операции над матрицами. Произведение матриц. Транспонирование матриц.
- •10. Понятие определителя свойств.
- •11.Способы построения обратной матрицы.
- •17. Решение однородных систем линейных уравнений.
- •21. Прямоугольные декартовы координаты вектора.
- •27. Критерий компланарности трех векторов.
- •34. Монотонные последовательности
- •38. Основные св-ва пределов функций.
- •39. Замечательные пределы
- •II Замечательный предел
- •42. Дифференциал ф-ции и геом.Смысл
- •43. :Основные теоремы диференц. Вычисления
- •45. .Первообразная функция и неопределенный интеграл.
- •50. Опр.Инт. С переем. Верхним пределом.Ф-ла Ньютона-Лейбница
- •53,56. Понятие числового ряда и его сходимость.
4.Эллипс и его каноническое уравнение
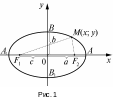 Эллипсом
называется
множество точек плоскости, сумма
расстояний от каждой из которых до двух
заданных точек
Эллипсом
называется
множество точек плоскости, сумма
расстояний от каждой из которых до двух
заданных точек
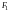 и
и
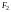 ,
называемых фокусами, есть величина
постоянная, равная
,
называемых фокусами, есть величина
постоянная, равная
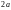 .
.
Выведем
уравнение эллипса. Для этого выберем
декартову систему координат
так, чтобы ось
проходила через фокусы
и
,
расстояние между которыми обозначим
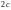 ,
а начало координат О
находилось в середине отрезка
,
а начало координат О
находилось в середине отрезка
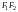 (рис. 1).
(рис. 1).
Тогда
фокусы будут иметь координаты:
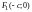 и
и
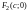 (рис. 1). Если
(рис. 1). Если
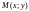 – произвольная точка эллипса, то согласно
его определению, имеем:
– произвольная точка эллипса, то согласно
его определению, имеем:
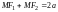 . (2)
. (2)
По формуле расстояния между двумя точками имеем
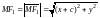 ,
,
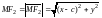 . (3)
. (3)
Подставляя (3) в (2), будем иметь
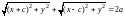 . (4)
. (4)
Уравнение (4) и есть уравнение эллипса. Приведем его к так называемому каноническому виду. Из (4) имеем
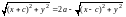 .
.
Возведя обе части последнего равенства в квадрат, получим
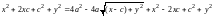 .
.
Отсюда
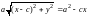 , (5)
, (5)
или, возведя обе части равенства (5) в квадрат, будем иметь
 . (6)
. (6)
Из (6) получаем
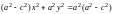 . (7)
. (7)
Так
как
 ,
то
,
то
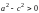 .
Обозначим
.
Обозначим
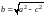 ,
тогда (7) примет вид
,
тогда (7) примет вид
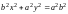 . (8)
. (8)
Разделив
обе части (8) на
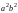 ,
получим уравнение эллипса вида:
,
получим уравнение эллипса вида:
. (9)
Показано,
что любая точка эллипса удовлетворяет
уравнению (9).
Покажем теперь обратное: любая точка
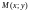 ,
удовлетворяющая
уравнению (9), принадлежит эллипсу, т.е.
удовлетворяет
соотношению (2). Из уравнения (9) получаем
,
удовлетворяющая
уравнению (9), принадлежит эллипсу, т.е.
удовлетворяет
соотношению (2). Из уравнения (9) получаем
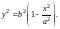
Используя
это соотношение и учитывая, что
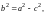 находим
находим
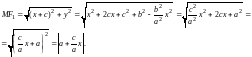
Так
как, в силу равенства (9),
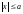 и, кроме того,
и, кроме того,
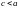 ,
то
,
то
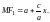
Аналогично
можно получить формулу
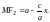 Складывая последние
два равенства, получаем равенство (2).
Складывая последние
два равенства, получаем равенство (2).
Итак,
соотношение (9) является уравнением
эллипса. Оно называется
каноническим
уравнением эллипса. Такой
эллипс изображен на рис. 1. Эллипс
симметричен относительно обеих осей
координат. Из уравнения (9) при
получаем:
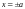 ,
т.е. эллипс пересекает ось
в двух точках:
,
т.е. эллипс пересекает ось
в двух точках: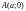 и
и
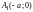 ;
при
получаем:
;
при
получаем:
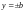 ,
т.е. эллипс пересекает ось
в
двух точках:
,
т.е. эллипс пересекает ось
в
двух точках:
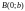 и
и
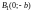 .
Эти четыре точки называют вершинами
эллипса.
Отрезок
.
Эти четыре точки называют вершинами
эллипса.
Отрезок
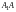 называется
большой осью
эллипса, а
отрезок
называется
большой осью
эллипса, а
отрезок
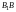 – его малой
осью. Значит,
– длина большой полуоси эллипса,
– длина малой полуоси эллипса.
– его малой
осью. Значит,
– длина большой полуоси эллипса,
– длина малой полуоси эллипса.
Уравнение
(9) можно рассматривать и в случае
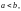 оно определяет эллипс с большой полуосью
оно определяет эллипс с большой полуосью
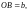 фокусы такого эллипса лежат на оси Oy.
фокусы такого эллипса лежат на оси Oy.
В
том случае, когда
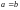 ,
уравнение (9) имеет вид
,
уравнение (9) имеет вид
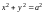 и
определяет окружность радиуса а
с центром в начале координат. В
этом случае
и
определяет окружность радиуса а
с центром в начале координат. В
этом случае
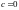 .
.
Эксцентриситетом эллипса называется отношение расстояния между фокусами к длине большой оси, т.е.
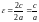 . (10)
. (10)
Поскольку
,
то для любого эллипса
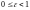 ,
причем случай
,
причем случай
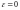 соответствует окружности.
соответствует окружности.
Геометрически
 характеризует степень сжатия эллипса.
Действительно, из (10) и равенства
характеризует степень сжатия эллипса.
Действительно, из (10) и равенства
 вытекает, что
вытекает, что
 .
.
Значит,
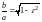 . (11)
. (11)
Из
(11) видно, что чем больше
,
тем меньше отношение
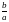 и тем больше вытянут эллипс. Две прямые,
перпендикулярные большой оси эллипса
и расположенные симметрично относительно
центра на расстоянии
и тем больше вытянут эллипс. Две прямые,
перпендикулярные большой оси эллипса
и расположенные симметрично относительно
центра на расстоянии
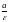 от него, называются директрисами
эллипса.
от него, называются директрисами
эллипса.
Если эллипс задан каноническим уравнением (8), то уравнения директрис имеют вид
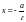 и
и
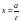 . (12)
. (12)
Так
как
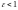 ,
то
,
то
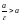 .
Откуда заключаем, что правая директриса
расположена
правее правой вершины эллипса, а левая
– левее его левой
вершины. Важность понятия директрис
будет установлена позднее.
.
Откуда заключаем, что правая директриса
расположена
правее правой вершины эллипса, а левая
– левее его левой
вершины. Важность понятия директрис
будет установлена позднее.
