- •Поняття первісної та невизначеного інтеграла.
- •Основні властивості невизначеного інтеграла.
- •Деякі методи інтегрування Безпосереднє інтегрування.
- •Заміна змінної у невизначеному інтегралі.
- •Інтегрування частинами.
- •Визначений інтеграл Задача про площу криволінійної трапеції.
- •Поняття визначеного інтеграла.
- •Властивості визначеного інтеграла, які виражаються рівностями.
- •Властивості визначеного інтеграла, які виражаються нерівностями.
- •Метод інтегрування частинами.
- •Метод заміни змінної.
- •Обчислення площ плоских фігур за допомогою визначеного інтеграла.
- •Основні поняття
- •2. Диференціальні рівняння першого порядку
- •3. Інтегрування деяких типів диференціальних рівнянь першого порядку.
- •Основні поняття.
- •Диференціальне числення фдз. Частинні прирости, похідні та диференціали.
- •Диференційовність функції двох змінних.
- •Похідна за напрямком.
- •Градієнт.
- •Найважливіші властивості градієнту:
- •Частинні похідні вищих порядків.
- •Екстремуми функції двох змінних.
- •Умовний екстремум.
- •Найбільше і найменше значення функції в обмеженій замкненій області.
- •На стороні оа , тому знаходимо найбільше та найменше значення функції однієї змінної: на сегменті .
- •На стороні ав або , тому знаходимо найбільше та найменше значення функції однієї змінної: на сегменті .
- •На стороні ов , тому знаходимо найбільше та найменше значення функції однієї змінної: на сегменті .
Умовний екстремум.
При
розв’язуванні багатьох задач, зокрема
економічних, потрібно знаходити екстремум
функції
при певних додаткових обмеженнях,
наприклад, при умові накладення деякого
зв’язку на незалежні змінні
![]() .
Такі задачі називаються задачами
знаходження умовного екстремуму функції,
а рівняння
– рівнянням зв’язку.
.
Такі задачі називаються задачами
знаходження умовного екстремуму функції,
а рівняння
– рівнянням зв’язку.
Для розв’язування задач на пошук умовних екстремумів застосовують метод виключення змінної (якщо це можливо) або більш універсальний метод Лагранжа (часто називають метод множників Лагранжа).
Суть першого методу полягає в тому, що із рівняння зв’язку одну із змінних виражають через іншу, підставляють у функцію і задачу умовного екстремуму зводять до задачі пошуку екстремуму функції однієї змінної.
Метод виключення при знаходженні умовного екстремуму застосовується не завжди, оскільки рівняння зв’язку не завжди можна розв’язати відносно однієї із змінних. Методика знаходження умовного екстремуму, вільна від цього недоліку, була запропонована Лагранжем. Основою методу Лагранжа є наступна теорема.
Теорема.
Якщо
функція
має в точці
екстремум при умові
і
![]() ,
то існує число
,
то існує число
![]() таке, що упорядкована трійка дійсних
чисел
таке, що упорядкована трійка дійсних
чисел
![]() є розв’язком системи рівнянь:
є розв’язком системи рівнянь:
![]() де
де
![]() – функція Лагранжа.
– функція Лагранжа.
Ця теорема є лише необхідною умовою існування екстремуму.
Схема методу Лагранжа.
1. Скласти функцію Лагранжа і знайти її стаціонарні точки .
2.
Для
кожної стаціонарної точки
,
підставивши
у вираз
![]() ,
одержимо функцію двох змінних
,
одержимо функцію двох змінних
![]() .
.
3.
Для
отриманої функції
знайти диференціал другого порядку
![]() в точці
і виразити його через приріст тільки
однієї змінної (тобто,
в точці
і виразити його через приріст тільки
однієї змінної (тобто,
![]() або
або
![]() ), використовуючи умову
.
Оцінюючи знак
,
можна зробити висновок про наявність
умовного мінімума або максимума в точці
.
), використовуючи умову
.
Оцінюючи знак
,
можна зробити висновок про наявність
умовного мінімума або максимума в точці
.
Зауваження
.
Умова
![]() еквівалентна умові
еквівалентна умові
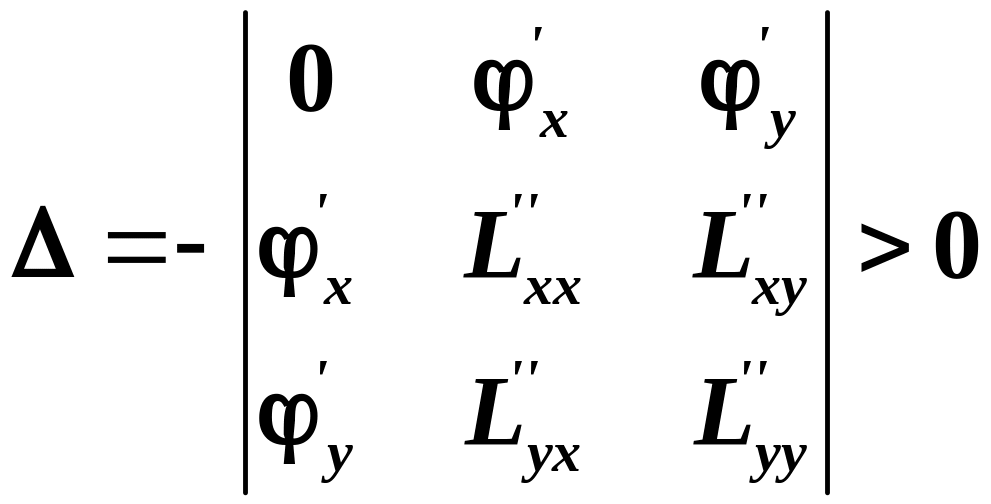 ,
а
умова
,
а
умова
![]() еквівалентна умові
еквівалентна умові
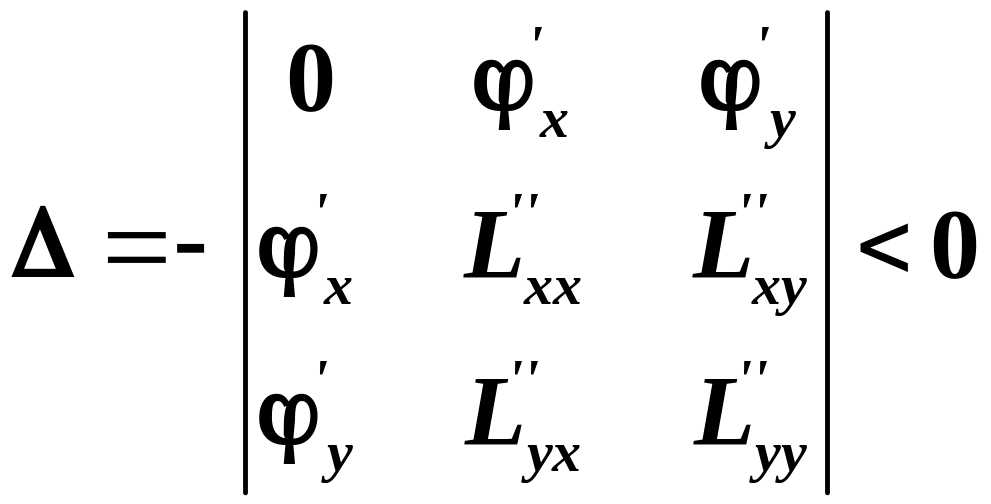 .
.
Приклад
.
Знайти екстремум функції
![]() при умові
при умові
![]() .
.
Розв’язування.
Оскільки з рівняння зв’язку легко виразити одну змінну через іншу, то використаємо метод виключення.
![]() тоді
тоді
![]() або
або
![]() .
.
Задача звелася до знаходження екстремуму функції однієї змінної.
За відомою схемою дослідження функції на екстремум маємо:
![]() ;
;
![]() ;
;
![]()
![]()
критична
точка
![]() – підозріла на екстремум за теоремою
(необхідна умова екстремума).
– підозріла на екстремум за теоремою
(необхідна умова екстремума).
Оскільки
при переході через критичну точку
похідна
![]() змінює знак з “–” на “+”, то за першою
достатньою умовою існування екстремуму
- точка мінімума.
змінює знак з “–” на “+”, то за першою
достатньою умовою існування екстремуму
- точка мінімума.
![]() .
.
Знайдемо значення при : |
|
Отже,
функція
має умовний мінімум у точці
![]() .
.
Відповідь:
![]() при умові
при умові
![]() .
.
Приклад
.
Знайти екстремум функції
![]() при умові
при умові
![]() .
.
Розв’язування.
Метод
виключення змінних.
Із умови
![]() .
Підставляємо у
і досліджуємо функцію однієї змінної
.
Підставляємо у
і досліджуємо функцію однієї змінної
![]() на екстремуми. Похідна
на екстремуми. Похідна
![]() ,
її критичні точки
,
її критичні точки
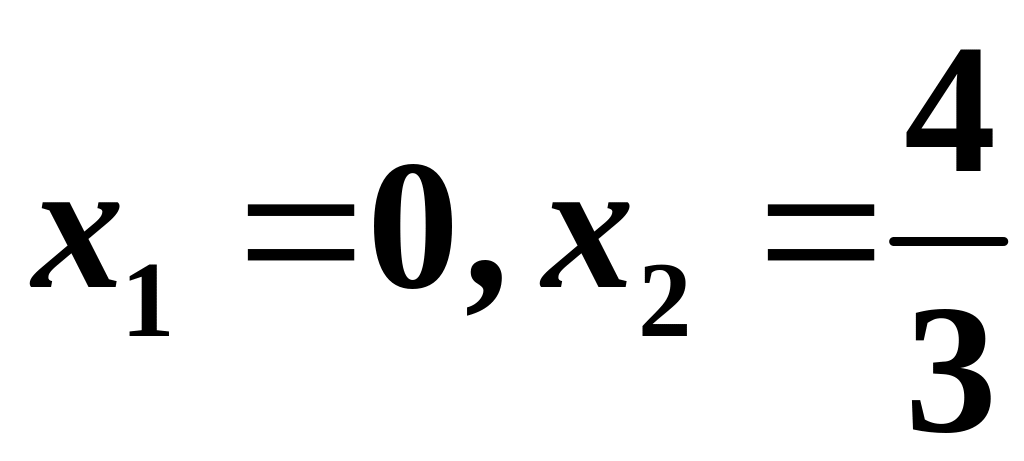 - підозрілі на екстремуми. Похідна
другого порядку
- підозрілі на екстремуми. Похідна
другого порядку
![]() в першій критичній точці
в першій критичній точці
![]() ,
тому за другою достатньою умовою
екстремума
,
тому за другою достатньою умовою
екстремума
![]() є точкою мінімума. В другій критичній
точці
є точкою мінімума. В другій критичній
точці
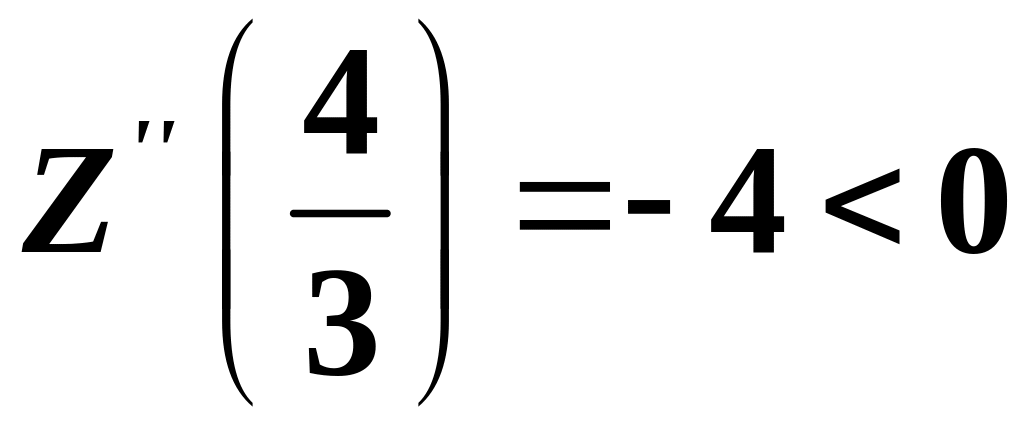 ,
тому за другою достатньою умовою
екстремума
,
тому за другою достатньою умовою
екстремума
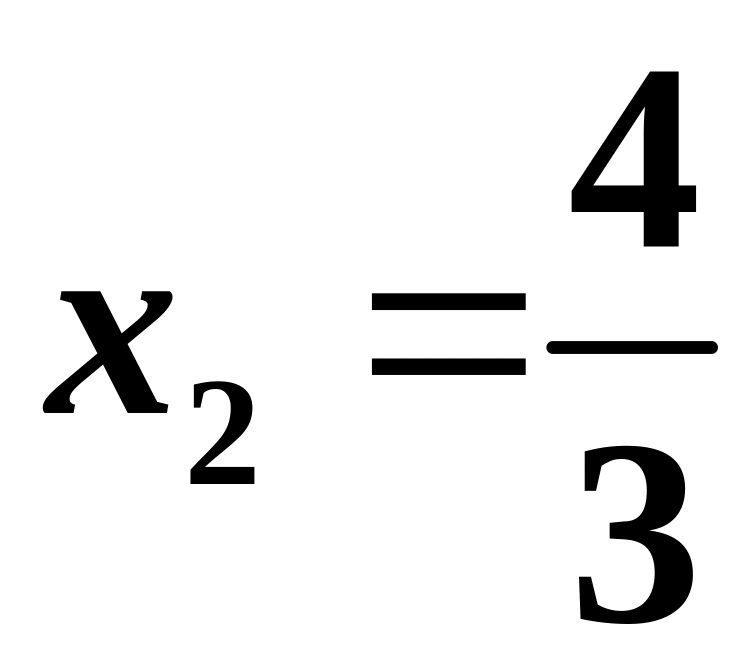 є точкою максимума. Отже, умовними
екстремумами функції є
є точкою максимума. Отже, умовними
екстремумами функції є
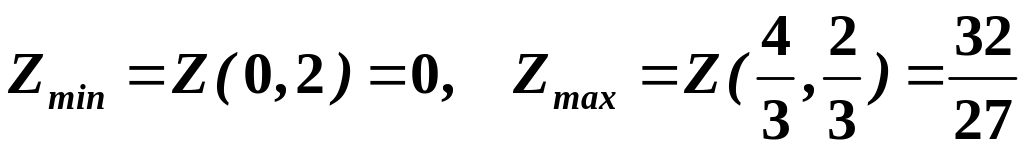 при умові
.
при умові
.
Метод Лагранжа. Складемо функцію Лагранжа:
![]() ,
,
де
![]() , а
, а
![]() .
.
![]() .
.
Знайдемо стаціонарні точки:
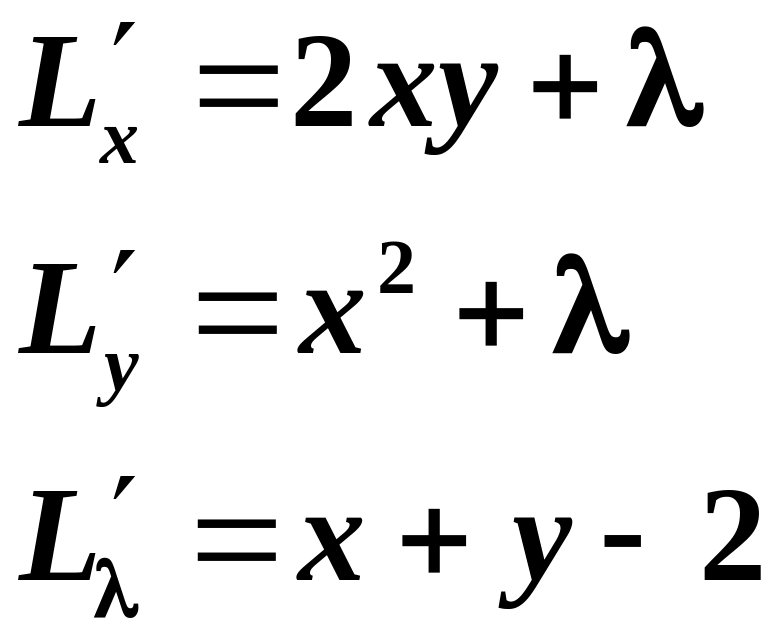
![]()
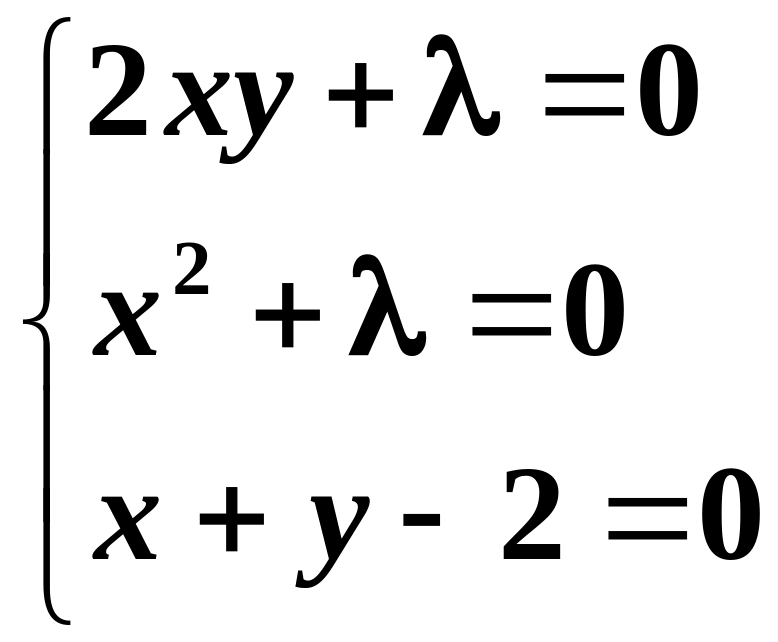 .
.
Віднімаючи перші два рівняння, отримаємо:
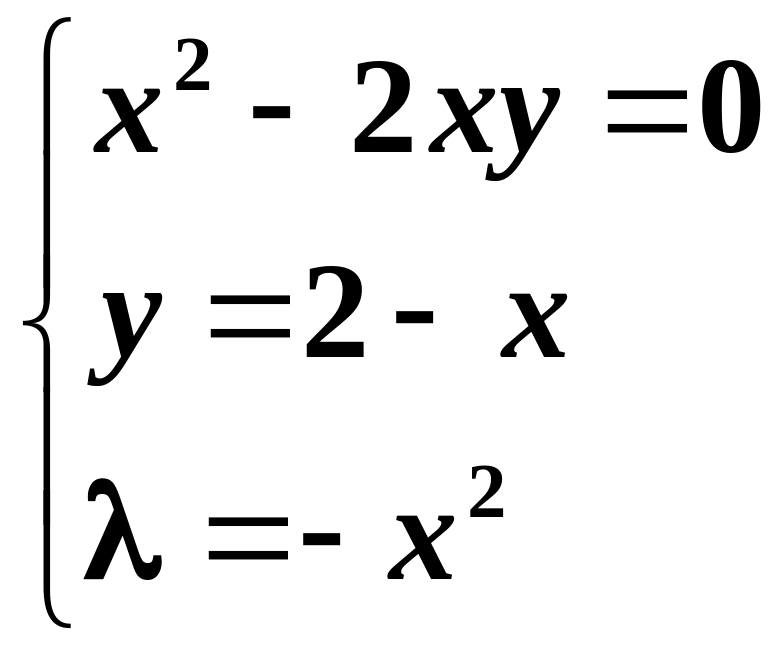
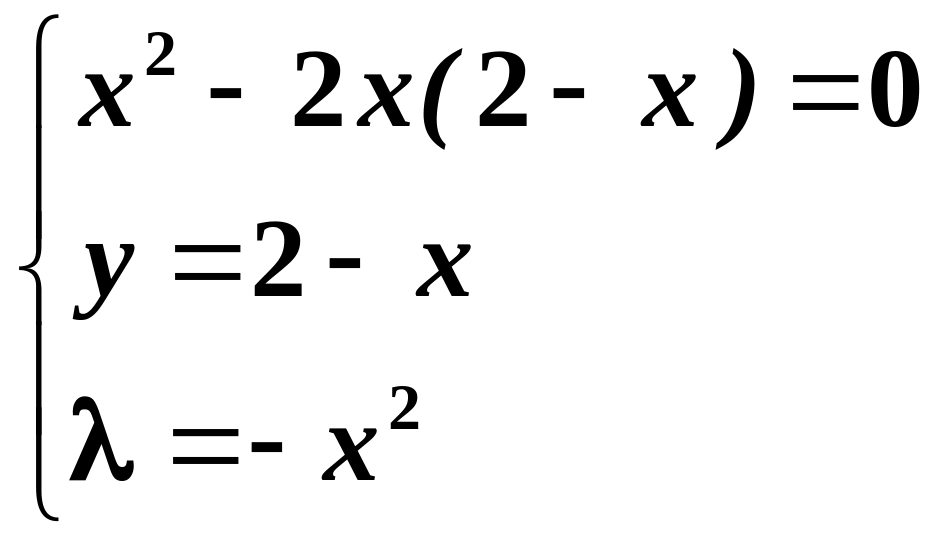
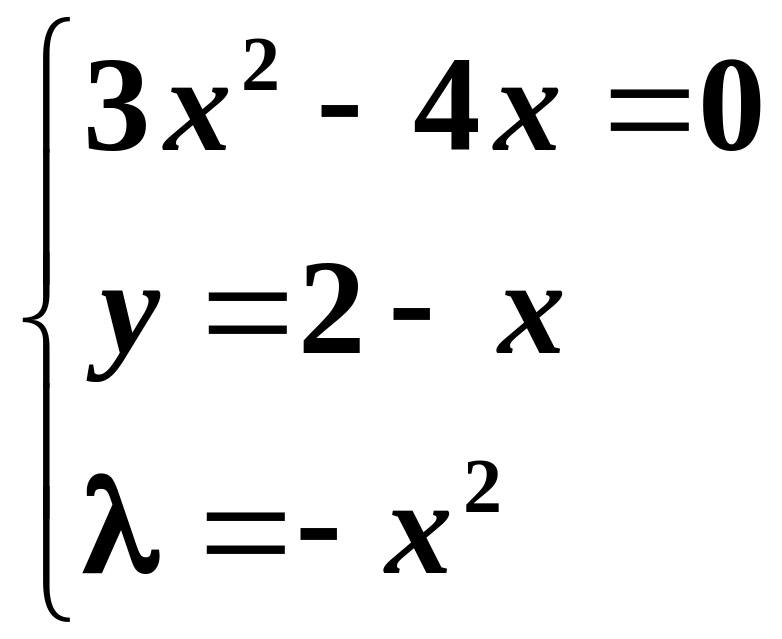
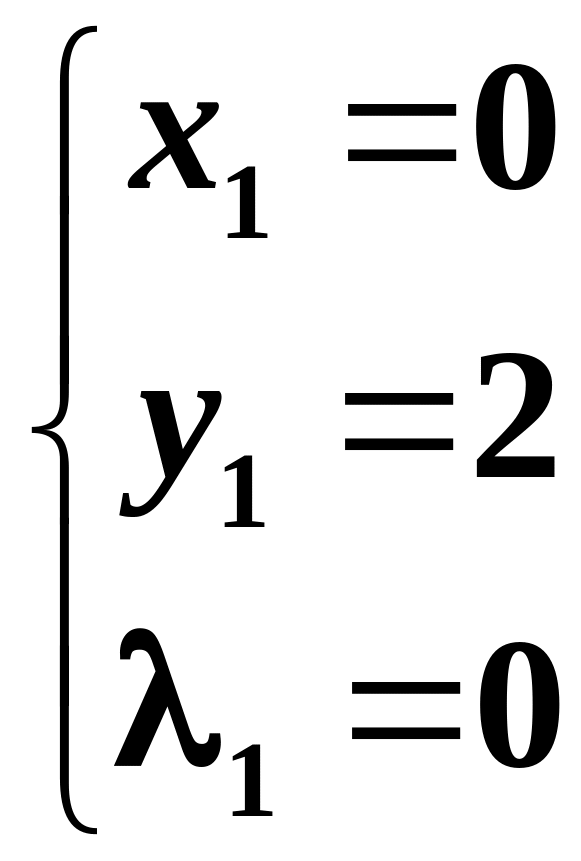
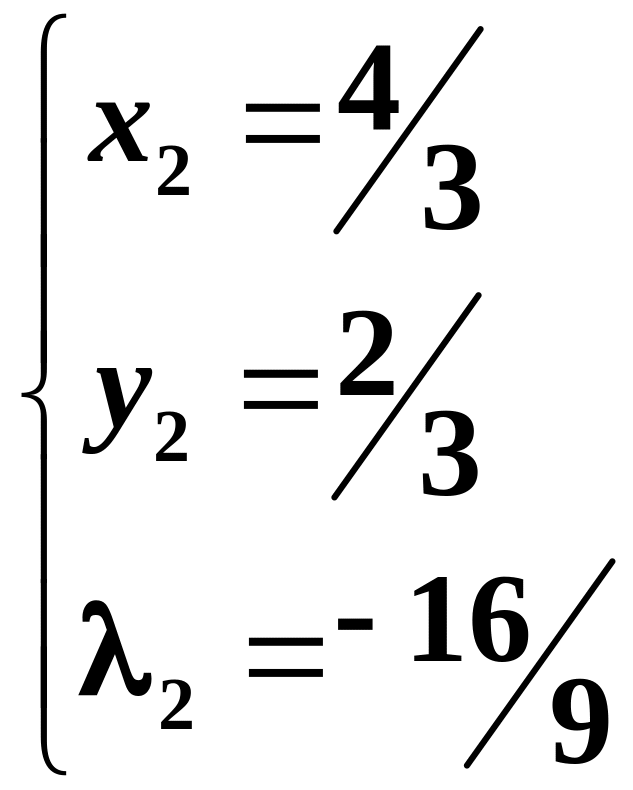
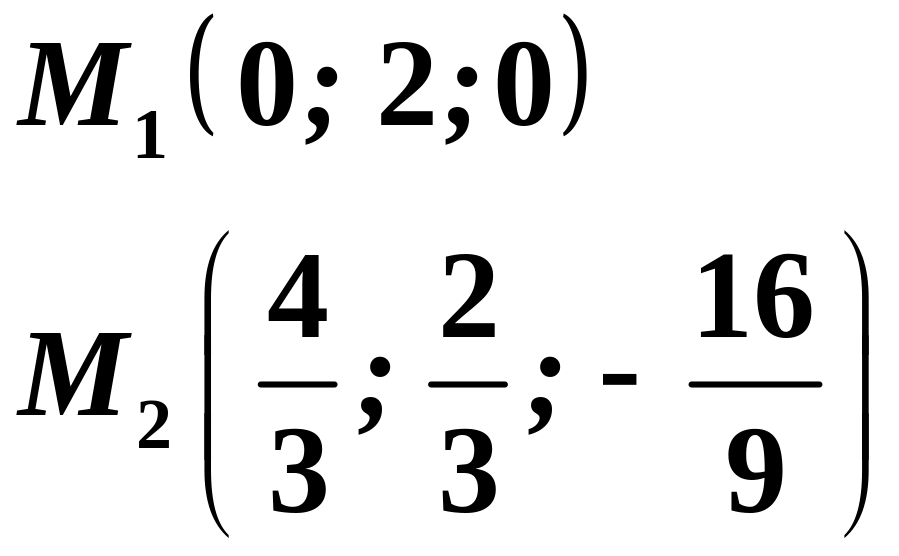 – стаціонарні
точки.
– стаціонарні
точки.
Дослідимо
диференціал другого порядку функції
двох змінних
![]() .
.
Частинні похідні другого порядку:
![]() ;
;
![]() ;
;
![]() .
.
Вираз для диференціалу другого порядку:
![]() .
.
Диференціюванням умови дістаємо:
![]() .
.
Враховуючи зв’язок між приростами аргументів, маємо:
![]() .
.
Оскільки
при
![]() :
:
![]() при будь-яких приростах аргументів, то
при будь-яких приростах аргументів, то
![]() - точка умовного мінімуму функції
при умові
.
- точка умовного мінімуму функції
при умові
.
При
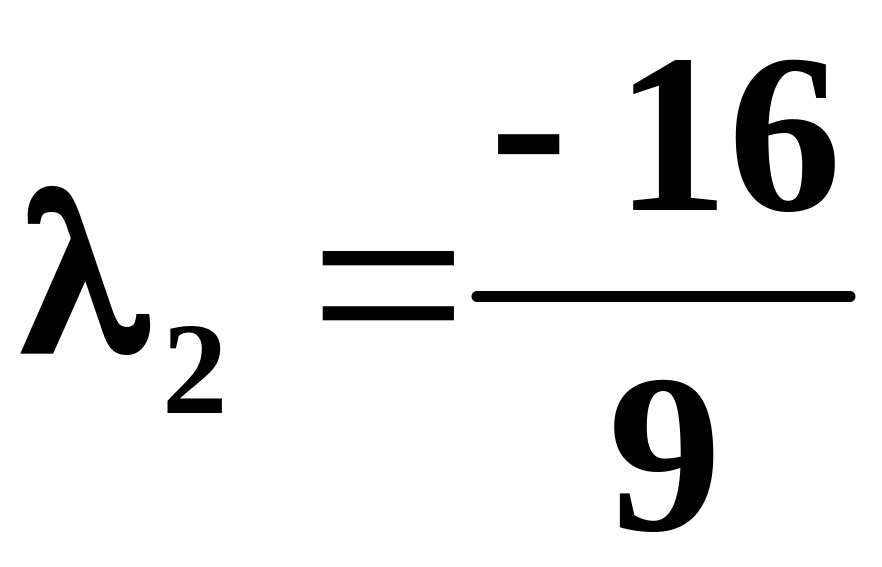 :
:
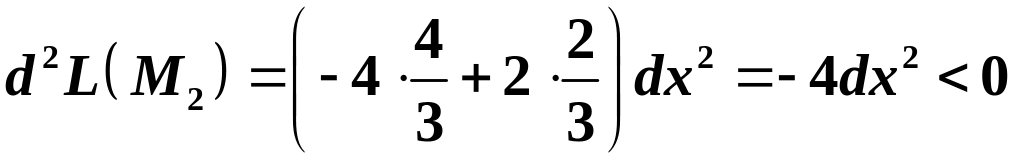 при будь-яких приростах аргументів, то
- точка умовного максимума функції
при умові
.
при будь-яких приростах аргументів, то
- точка умовного максимума функції
при умові
.
Зауваження . Часто для оцінки знаку диференціалу другого порядку в точці немає необхідності використовувати умову і виражати диференціали аргументів один через інший (див. вищенаведені приклади).