
21. непрерывные случайные величины. Числовые характеристики случайных величин: дисперсия непрерывной случайной величины и её свойства.
Непрерывной случайной величиной называют величину которая может принимать все значения из некоторого бесконечного промежутка. Очевидно число возможных значений непрерывной случайной величины бесконечно.
Более точная формулировка: случайную величину называют непрерывной, если функция её распределения есть непрерывная, кусочно-дифференцируемая функция с непрерывной производной.
Дисперсией непр. случ велич. назыв. математ ожидан. кввадрата её отклон..
если возм-ые знач
Х прин отрзку [a,b]
то
![]() если возможные значения принадл. всей
оси x, то
если возможные значения принадл. всей
оси x, то
![]()
22.
Элементарные
функции алгебры логики Обозначения:
E2={0,1};
Е![]() =
E2E2...E2
– прямое
произведение n
сомножителей; (x
=
E2E2...E2
– прямое
произведение n
сомножителей; (x![]() ,..,xn)
E2,
| E2|
– мощность E2,
|E2|=2,
тогда |Е
|=2n.
Определение
1. Функцией
алгебры логики называется закон,
осуществляющий отображение Е
,..,xn)
E2,
| E2|
– мощность E2,
|E2|=2,
тогда |Е
|=2n.
Определение
1. Функцией
алгебры логики называется закон,
осуществляющий отображение Е
![]() E2,
причем отображение всюду определено и
функционально. Так как множество Е
E2,
причем отображение всюду определено и
функционально. Так как множество Е![]() конечно,
то задать отображение Е
E2,
означает задать множество наборов
из Е
и для каждого набора указать его образ
в Е
2.
конечно,
то задать отображение Е
E2,
означает задать множество наборов
из Е
и для каждого набора указать его образ
в Е
2.
Конъюнкция
 эту операцию называют логическим
умножением
эту операцию называют логическим
умножением сложение
сложение
 по модулю два
по модулю два

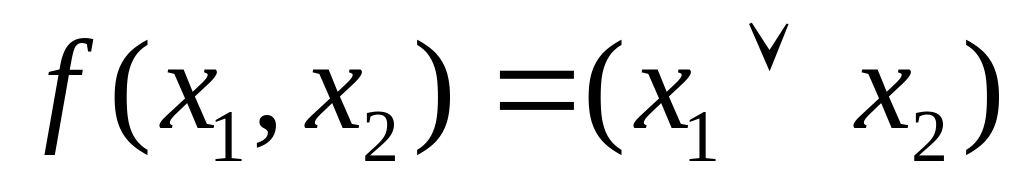 дизъюнкция
– логическое сложение
дизъюнкция
– логическое сложение отрицание
дизъюнкции
отрицание
дизъюнкции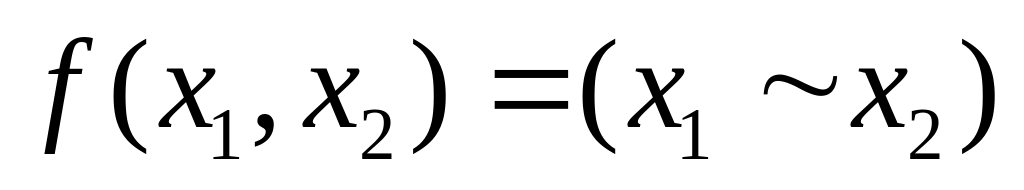



Cимволы
![]() ,
,![]()
![]()
участвующие в обозначениях
элементарных функций, называются
логическими связками или просто связками.
Переменные 0 и 1 называются логическими
или булевыми переменными, причем 0
соответствует «лжи» , а 1 – «истине», а
функции алгебры логики называются еще
и блевыми функциями.
участвующие в обозначениях
элементарных функций, называются
логическими связками или просто связками.
Переменные 0 и 1 называются логическими
или булевыми переменными, причем 0
соответствует «лжи» , а 1 – «истине», а
функции алгебры логики называются еще
и блевыми функциями.
23. числовые хар-ки дискр случ величин: дисперсия дискр случ велич.
дисперсией(рассеянием) дискретной случайной величины назывся математ ожидание квадрата отклонен случайной от её математич ожидания:
![]() пусть случайная
величина задана законом распределения
пусть случайная
величина задана законом распределения
![]()
тогда квадрат отклон имеет следущ закон распределен
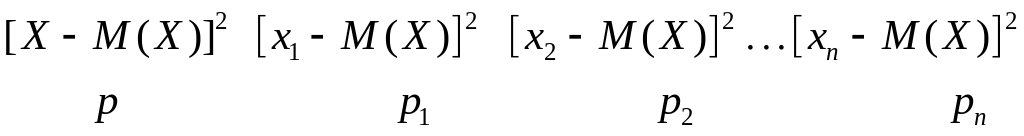
по определению
дисперсии,
![]()
Т.о. чтобы найти дисперс достаточно вычислить сумму произведений возм знач-ий квадрата отклонен-я на их вероятности.
24. формульное задание функций алгебры логики. упрощение записи формул. некоторые свойства элементарных функций
дадим индуктивное определение формулы над
Определение:
пусть
![]() ,
тогда
,
тогда
каждая функция
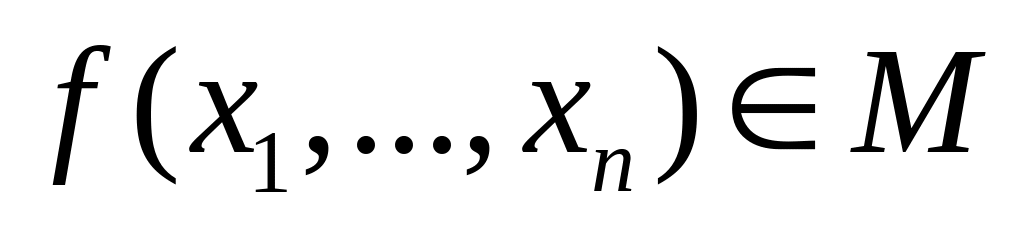 называется
формулой над М;
называется
формулой над М;пусть
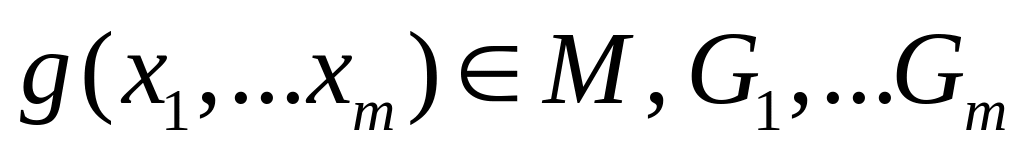 -
либо переменные, либо формулы над М.
тогда выражение
-
либо переменные, либо формулы над М.
тогда выражение
 -
формула над М
-
формула над М
Формулы будем
обозначать заглавными буквами:
![]() ,
имея ввиду функции, участвующие в
построении формулы, или
,
имея ввиду функции, участвующие в
построении формулы, или
![]() имея
ввиду переменные, вошедшие в формулу.
имея
ввиду переменные, вошедшие в формулу.
![]() -
формулы, участвующие в построение
-
формулы, участвующие в построение
![]() называются подформулами.
называются подформулами.
множество всех формул над М обозначим через <М>
Определение 2:
две формулы N и D из <М> называются равными N=D или эквивалентными N~D или эквивалентными, если функции, реализуемые ими, равны.
Упрощение записи формул:
внешние скобки можно опускать;
приоритет применения связок возрастает в следующем порядке:
![]() ~
→
~
→
![]()
связка над одной переменной сильнее всех связок;
если связка стоит над формулой, то сначала выполняется формула затем отрицание;
если нет скобок, то операции ~ и → выполняются в последнюю очередь.
Некоторые свойства элементарных функций
Идемпотентность
 :
:
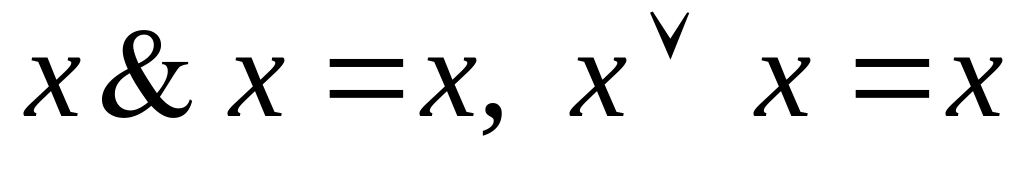
коммутативность

Ассоциативность
 поэтому
в формулах вида xyz можно не ставить
никаких скобок.
поэтому
в формулах вида xyz можно не ставить
никаких скобок.дистрибутивность
 по
отношению к
по
отношению к
 :
: 
по отношению к :
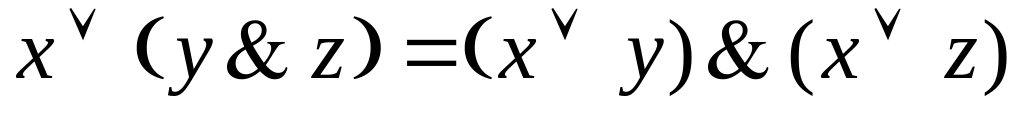
по отношению к
 :
: 
Инволюция:

Правило Де Моргана:

Законы действия с 0 и 1:
![]()
Самодистрибутивность импликации:

25. Дискретные случайные величины. числовые характеристики дискретных случайных величин: математическое ожидание дискр случ величины, свойства математического ожидания.
математическим ожиданием дискретной случайной величины называют сумму произведений всех её возможных значений на их вероятности.
пусть случайная
величина X может принимать только
значения
![]() ,
вероятности которых соответственно
равны
,
вероятности которых соответственно
равны
![]() .
тогда математическое ожидание M(X)
величины Х определяется равенством
.
тогда математическое ожидание M(X)
величины Х определяется равенством
![]()
если дискретная случайная величина Х принимает счетное множество возможных значений то
![]() причем
математическое ожидание существует,
если ряд в правой части равенства
сходится абсолютно.
причем
математическое ожидание существует,
если ряд в правой части равенства
сходится абсолютно.
Свойства математического ожидания
1) Математическое ожидание постоянной величины равно самой постоянной.
![]()
2) Постоянный множитель можно выносить за знак математического ожидания.
![]()
3) Математическое ожидание произведения двух независимых случайных величин равно произведению их математических ожиданий.
![]()
Это свойство справедливо для произвольного числа случайных величин.
4) Математическое ожидание суммы двух случайных величин равно сумме математических ожиданий слагаемых.
![]()
Это свойство также справедливо для произвольного числа случайных величин.
Пусть производится п независимых испытаний, вероятность появления события А в которых равна р.
Теорема. Математическое ожидание М(Х) числа появления события А в п независимых испытаниях равно произведению числа испытаний на вероятность появления события в каждом испытании.
![]()
Однако, математическое ожидание не может полностью характеризовать случайный процесс. Кроме математического ожидания надо ввести величину, которая характеризует отклонение значений случайной величины от математического ожидания.
Это отклонение равно разности между случайной величиной и ее математическим ожиданием. При этом математическое ожидание отклонения равно нулю. Это объясняется тем, что одни возможные отклонения положительны, другие отрицательны, и в результате их взаимного погашения получается ноль.
26,
Принцип двойственности Определение
1. Функции f*(x1, ..., xn)
называется двойственной к функции f(x1,
..., xn), если f*(x1,
..., xn) =
![]() (
(![]() 1,
...,
n).
1,
...,
n).
Пример 1. Покажем с помощью таблицы истинности, что константа 0 двойственна к 1:
-
x
f
f*
0
1
0
0
1
1
Функции f(x) = x и g(x) = двойственны сами себе:
-
x
f
f*
g
g*
0
1
0
1
0
1
1
0
1
0
так
как f*(0)=![]() (1).
(1).
Определение 2. Если f*(x1, ..., xn) = f(x1, ..., xn), то f(x1, ..., xn) называется самодвойственной.
Пример 2. Покажем, что f(x1,x2,x3)=x1x2x3 – самодвойственна:
-
x1
x2
x3
f
f*
0
0
0
0
1
1
1
1
0
0
1
1
0
0
1
1
0
1
0
1
0
1
0
1
0
1
1
0
1
0
0
1
0
1
1
0
1
0
0
1
Если
f*– самодвойственна, то
![]() (
(![]() 1,
...,
n)
= f(x1, ..., xn),
т.е. на противоположных наборах функция
принимает противоположные значения.
1,
...,
n)
= f(x1, ..., xn),
т.е. на противоположных наборах функция
принимает противоположные значения.
Пример 3. Покажем, что функция х1х2 двойственна к x1&x2, функция х1 х2 двойственна к функции x1|x2.
-
x1 x2
f=х1х2
f*
g=x1|x2
g*=x1 x2
0 0
0 1
1 0
1 1
0
1
1
1
0
0
0
1
1
1
1
0
1
0
0
0
Теорема о двойственных функциях Если f* двойственна к f, то f двойственна к f*.
Доказательство.
f*(x1, ..., xn) =
(![]() 1,
...,
n).
Найдем двойственную функцию к f*,
т.е. (f*( x1, ..., xn))*
= (
(
1,
...,
n))*
=
1,
...,
n).
Найдем двойственную функцию к f*,
т.е. (f*( x1, ..., xn))*
= (
(
1,
...,
n))*
=
![]() (
(![]() 1,
...,
1,
...,
![]() n)
= f(x1, .., xn).
n)
= f(x1, .., xn).
Предположим, что функция задана формулой. Можно ли найти по этой формуле двойственную функцию? Ответ на этот вопрос дает следующая теорема.
Принцип двойственности Теорема: Пусть функция h(x1, ..., xn) реализована формулой h(x1, ..., xn) = =g(G1, ..., Gm) = g(f1(x1, ..., xn), ..., fm(x1, ..., xn)), где какие-то переменные могут быть фиктивными. Тогда h*( x1, ..., xn) = g*(f1*( x1, ..., xn), ..., fm*(x1, …, xn)), это означает, что если функция задана некоторой формулой, то чтобы получить двойственную функцию, надо в этой формуле все знаки функций заменить на двойственные, 0 на 1, 1 на 0.
Доказательство.
h*(x1, ..., xn) =
![]() (
1,
...,
n)
=
(
1,
...,
n)
=
![]() (f1(
1,
...,
n),
..., fm(
1,
...,
(f1(
1,
...,
n),
..., fm(
1,
...,
![]() n))
=
n))
=
![]()
..
n
.
..
n
.
![]()
.
n
g
.
n
g![]()
..
.. ![]()
g*(f1*(
x1, ..., xn), ..., fm*(
x1, ..., xn)), что и
требовалось доказать.
g*(f1*(
x1, ..., xn), ..., fm*(
x1, ..., xn)), что и
требовалось доказать.
Если функция h(x1, ..., xn) реализуется формулой N[f1, ..., fn], то формулу, полученную из N заменой fi, входящих в нее, на fi* и реализующую функцию h*(x1, ..., xn), будем называть двойственной и обозначать N*(x1, ..., xn).
Лемма
о несамодвойственной функции Подстановкой
функций
![]() и
и
![]() в несамодвойственную функцию можно
получить одну из констант.
в несамодвойственную функцию можно
получить одну из констант.
Доказательство.
Пусть
![]() – несамодвойственная функция. Тогда
существует набор
– несамодвойственная функция. Тогда
существует набор
![]() ,
для которого
,
для которого
![]() .
Построим функцию
.
Построим функцию
![]() ,
заменив единицы в
,
заменив единицы в
![]() на
,
а нули – на
.
Так как
на
,
а нули – на
.
Так как
![]() ,
то
,
то
![]() .
Заметим, что
.
Заметим, что
![]() .
.
Тогда
![]() ,
т.е.
,
т.е.
![]() .
Следовательно, функция
есть одна из констант.
.
Следовательно, функция
есть одна из констант.
