1. 2. Предел функции
1. При вычислении предела функции
обычно руководствуются следующими
соображениями.
1) Для всякой элементарной функции
справедливо равенство
при любых
.
2) Если
и функция
определена в некоторой окрестности
точки
,
то вычисление предела (раскрытие
неопределенностей вида
)
— достаточно сложная задача. Рассмотрим
типичные случаи.
2. Рациональные функции.
Если рациональная функция имеет вид
,
где
и
- некоторые многочлены, причем
,
то возможны два случая:
а)
,
тогда
,
и б)
;
в этом случае непосредственная подстановка
в дробь
приводит к неопределенности вида
,
которую мы будем условно записывать
так:
.
Для раскрытия неопределенности, как
правило, приходится разлагать числитель
и знаменатель на множители и сокращать
на линейный множитель
.
Примечание.
Если
,
то
принадлежит области определения D
функции
,
и поэтому ее предел в точке
равен значению функции:
.
Пример 2.
Вычислить:
.
Решение.
.
3. Иррациональные функции. Если неопределенное выражение содержит иррациональность, то, умножая на сопряженное выражение числитель и знаменатель, переводят иррациональность из знаменателя в числитель или наоборот.
Пример 3.
Вычислить:
.
Решение.
.
4. Предел при
.
При вычислении предела при
делают замену переменных
(тогда
)
либо делят числитель и знаменатель на
наивысшую степень
,
входящую в выражение.
Пример 4. Вычислить
.
Решение.
.
5. Первый замечательный предел
(1)
используется при раскрытии неопределенностей
вида
в тригонометрических выражениях.
Пример 5. Вычислить
.
Решение.
.
Пример 6. Вычислить
.
Решение.
.
6. Второй замечательный предел
(2)
используют при вычислении пределов
вида
,
где
(что дает неопределенность вида
).
Пример 7. Вычислить
.
Решение.
.
1.3. Непрерывность функции
1. Определение.
Функция
с областью определения
называется непрерывной в точке
,
если выполнены следующие три условия:
а) функция
определена в точке
,
т. е.
;
б) существует
;
в)
.
2. Теорема. Все элементарные функции непрерывны в области определения.
3. Точки разрыва. Если не выполнено хотя бы одно из условий определения (1), точка называется точкой разрыва функции . При этом различают следующие случаи:
а)
существует, но функция не определена в
точке
или
.В
этом случае
называется точкой устранимого разрыва.
б) не существует, но при этом существуют оба односторонних предела и они не равны друг другу:
,тогда
точка
называется точкой разрыва I
рода.
в) в остальных случаях точка называется точкой разрыва II рода.
Пример 8. Исследовать на непрерывность функцию
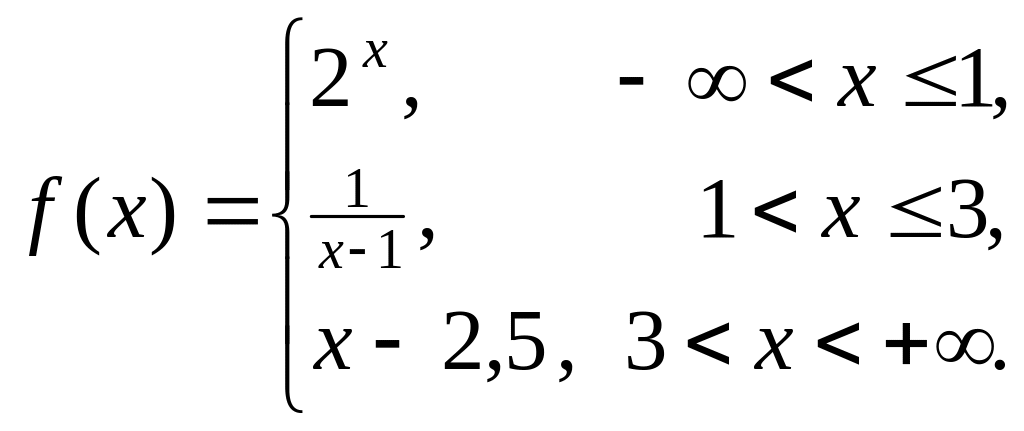
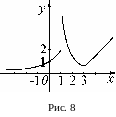Решение.
Функция задана на трех промежутках
разными формулами. На каждом из промежутков
функция непрерывна (см. рис. 8.). Рассмотрим
границы промежутков:
и
.
В точке
замечаем, что
.
Следовательно, — точка разрыва II рода. В точке вычисляем:
Таким образом, в точке функция непрерывна.