8. Реляционное исчисление с переменными-кортежами: основные определения, понятие атомов, правильно построенная формула.

В основе реляционной модели данных (РМД) лежат некоторые разделы математической теории отношений и математической логики. Манипуляционную часть РМД составляют спецификационные операторы, естественные для РМД и базирующиеся на концепциях теории множеств. Языки запросов в РМД разбиваются на два класса:

• алгебраические языки (реляционная алгебра), позволяющие выражать запросы с помощью специальных операторов, применяемых к отношениям;

• языки исчисления предикатов (реляционное исчисление), в которых запросы описывают требуемое множество кортежей путем спецификации предиката, которому должны удовлетворять эти кортежи.

Из приведенного определения следует:

• языки реляционной алгебры показывают, как получить результат;

• языки реляционного исчисления показывают, что должно быть получено.

Языки реляционного исчисления делятся на два класса: с переменными–кортежами и с переменными на доменах – в зависимости от того, что является примитивными объектами исчисления: кортежи или элементы доменов, являющиеся значениями некоторых атрибутов.

Реляционное исчисление лежит в основе декларативного подхода к формулировке запроса к БД, суть которого заключается в следующем: запросу к БД соответствует формула некоторой формально-логической теории, которая описывает свойства желаемого результата.

Ответом на запрос служит множество объектов из области интерпретации (которой является БД), на котором истинна формула, соответствующая запросу.

В качестве такой формально-логической теории используется теория исчисления предикатов первого порядка, в которой формула задается в виде предиката.

Даны некоторые попарно не пересекающиеся произвольные множества D1, D2, …, Dn, Di  Dj = 0 для любых i  j, и переменные x1, x2, …, xn, принимающие значения из соответствующих множеств: xi  Di для любых i. Тогда предикатом (или предикатной функцией) называется функция P(x1, x2, …, xn), принимающая одно из двух значений – 1 или 0 (истина или ложь). Переменные x1, x2, …, xn называются предикатными переменными. Множества D1, D2, …, Dn образуют область интерпретации предиката.

В записи предиката, наряду с логическими операциями , , , смысл и использование которых традиционны, используются специальные операции – кванторы: всеобщности  и существования . Смысл использования кванторов следующий: x (f(x)) означает, что для всех значений x из области интерпретации формула f(x) имеет значение "истина"; x (f(x)) означает, что существует по крайней мере одно значение x из области интерпретации, для которого формула f(x) имеет значение "истина".

Для реляционного исчисления с переменными-кортежами областями определения переменных являются отношения БД, т.е. допустимым значением каждой переменной является кортеж некоторого отношения; Правильно построенные формулы служат для выражения условий, накладываемых на переменные (кортежи или на доменах).

Переменные-кортежи должны удовлетворять определенной схеме отношения R. Правильно построенная формула (wff – well formulated formula) определяет результаты отбора: выбираются те кортежи, для которых wff дает значение 1.

Обозначим правильно построенную формулу (предикат, значения которого 0 или 1) через (t). Рассмотрим правила построения (t).

I. Основой формулы являются атомы, которые могут иметь значения 0 или 1.

Существует три типа атомов формулы (t).

1. Пусть r(R) – некоторая реализация отношения, удовлетворяющая схеме R; t – некоторая переменная-кортеж, удовлетворяющая схеме R. Тогда r(t) – атом; означает, что t есть кортеж в реализации отношении r (т.е. формула истинна, если t  r).

2. Пусть r(R) – некоторая реализация отношения, удовлетворяющая схеме R; u и v – переменные-кортежи из отношения r(R) (т.е. u  r, v  r);  – арифметическая операция сравнения (, , , , , ); A, B – атрибуты схемы отношения R, сравнимые по операции ; тогда u[A]  v[B] – атом.

3. Пусть u – переменная-кортеж из отношения r(R) (т.е. u  r);  – арифметическая операция сравнения (, , , , , ); A, B – атрибуты схемы отношения R, сравнимые по операции ; c – константа из домена, на котором определен атрибут B; u[A]c (или cu[A]) – атом.

Запись u[A] означает «значение переменной-кортежа u по атрибуту A».

II. Формула реляционного исчисления (t), а также свободные и связанные вхождения переменных определяются по следующим рекурсивным правилам:

1. Каждый атом есть формула. Все вхождения переменных-кортежей, упомянутых в атоме, являются свободными. Например, формула r(t) утверждает, что переменная-кортеж t является кортежем отношения r(R).

2. Если x(R) – переменная-кортеж из отношения r со схемой R; (x) – формула, в которой переменная x имеет свободное вхождение; тогда x(R) ((x)). Данная формула утверждает, что существует хотя бы один кортеж x в отношении r(R), такой, что при подстановке его в формулу (x) вместо всех свободных вхождений x получим значение "истина". Например, формула x(R) (r(x)) утверждает, что отношение r не пусто (то есть, существует хотя бы один кортеж x, принадлежащий r).

3. Если x(R) – переменная-кортеж из отношения r со схемой R; (x) – формула, в которой переменная x имеет свободное вхождение; тогда x(R) ((x)). Данная формула утверждает, что для всех кортежей x из отношения r(R) при подстановке их в формулу (x) вместо всех свободных вхождений x получим значение "истина". Например, формула x(R) (x[A]  ) утверждает, что для всех кортежей значение атрибута A является обязательным.

4. Если (x) и (x) – формулы, тогда (x), (x)  (x), (x)  (x) – тоже формулы. Вхождения переменной x в эти формулы остаются свободными или связанными – такими, какими были в (x) или (x) соответственно.

5. Если (x) – формула, то ((x)) – тоже формула; вхождение переменной x остается свободным или связанным – таким, каким оно было в (x).

6. Ничто иное не является формулой.

При вычислении формул используется порядок старшинства операций, определяемый правилами построения формулы:

1. атомы, в которых могут быть использованы арифметические операции сравнения;

2. кванторы;

3. отрицание ()

4. операция "И" ()

5. операция "ИЛИ" ()

Скобки используются для изменения порядка вычисления формулы.

Выражение реляционного исчисления с переменными-кортежами имеет вид: {t(R) | (t)}, где t – переменная-кортеж, удовлетворяющая схеме отношения R; единственная переменная, имеющая свободное вхождение в формулу (t); (t) – правильно построенная формула. Интерпретация выражения реляционного исчисления: множество кортежей t, удовлетворяющих схеме отношения R, таких, для которых правильно построенная формула (t) истинна.

Пример:

Пусть есть отношение R(ИМЯ, СТИПЕНДИЯ); атрибут СТИПЕНДИЯ определен на домене D = {«да», «нет»}. Тогда выражение

{ t(ИМЯ) | x(R) (r(x)  x[СТИПЕНДИЯ] = «да»  x[ИМЯ] = t[ИМЯ]}

позволит получить из отношения имена всех студентов, получающих стипендию.

Выражение вида {t |  r(t) } в общем случае определяет бесконечное отношение, что недопустимо. Поэтому в реляционном исчислении ограничиваются рассмотрением так называемых безопасных выражений вида {t | (t) }, которые гарантированно дают ограниченное множество кортежей. В таких выражениях значения атрибутов кортежей t являются элементами некоторого ограниченного универсального множества – DOM().DOM() – унарное отношение, элементами которого являются символы, которые либо явно появляются в , либо служат компонентами какого-либо кортежа в некотором отношении R, упоминаемом в .

«Выражение {t | ( t)} реляционного исчисления с переменными-кортежами назовем безопасным, если выполняются следующие условия:

Всякий раз, когда t удовлетворяет (t), каждый компонент t есть элемент DOM().

Для любого подвыражения  вида (u) ((u)) каждый компонент u принадлежит DOM(), если u удовлетворяет .

Если для любого подвыражения  вида (u) ((u)) каждый компонент u не принадлежит DOM(), то u удовлетворяет .

Условия 2 и 3 позволяют устанавливать истинность квалифицированной формулы (u) ((u)) или (u) ((u)), рассматривая только u, составленные из принадлежащих DOM() символов. Например, любая формула ( u) (R(u)  …) удовлетворяет условию 2, а любая формула (u) (R(u)  …) – условию 3.»

Эквивалентность выражений реляционной алгебры и реляционного исчисления с переменными-кортежами (теорема): Если E – выражение реляционной алгебры, то 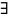эквивалентное ему безопасное выражение реляционного исчисления с переменными-кортежами.

Выражение реляционной алгебры	Выражение реляционного исчисления с переменными-кортежами
Объединение: r1  r2, r1(R), r2(R)	{x(R) | r1(x)  r2(x) }
Разность: r1 – r2 , r1(R), r2(R)	{x(R) | r1(x)  r2(x) }
Пересечение: r1  r2, r1(R), r2(R)	{x(R) | r1(x)  r2(x) }
Декартово произведение: r1  r2, r1(R1), r2(R2)	{x(R1R2) | u(R1) v(R2) (r1(u)  r2(v)  x[R1] = u{r1]  x[R2] = v[R2]) }
Проекция: L(r), r(R), L  R	{t(L) | u(R) (r(u)  u[L] = t[L] }
Выбор: F(r), r(R)	{ t(R) | r(t)  F’ ) }
Естественное соединение: r1 r2, r1(AB), r2(BC)	{ t(ABC) | u(AB) v(BC) ( r1(u)  r2(v)  u[B] = v[B]  t[AB] = u[AB]  t[C] = v[C]) }
Деление: r1  r2, r1(AB), r2(B)	{ t(A) | x(B) (r2(x)  y(AB) (r1(y)  y[B] = x[B]  y[A] = t[A] }