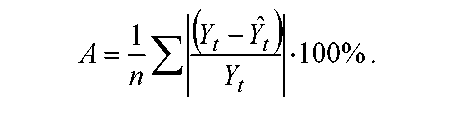- •11. Оценка дисперсии ошибок.
- •12. Оценка существенности параметров линейной регрессии и корреляции
- •13. Интервалы прогноза по линейному уравнению регрессии
- •14. Нелинейная регрессия. Линеаризируемые и нелинеаризируемые модели.Эластичность
- •15. Корреляция для нелинейной регрессии. Средняя ошибка аппроксимации.
- •16. Множественная регрессия. Спецификация модели. Отбор факторов.
- •17. Мнк для множественной регрессии. Мультиколлинеарность ее последствия.
- •19. Множественная корреляция. Скорректированный индекс детерминации.
- •20. Частная корреляция при множественной регрессии. Прцедура пошагового отбора переменных
14. Нелинейная регрессия. Линеаризируемые и нелинеаризируемые модели.Эластичность
Лин.
регрессия явл. частным, и не самым
распростр. случаем
регрессии. Чаще строят нелин. модели.
Например: с помощью гиперболы
![]() ,
полиномиал.:
,
полиномиал.:
![]() (чаще
2-ой степени, реже 3-ей) и т.д. Различают
2
класса нелин. регрессий:
(чаще
2-ой степени, реже 3-ей) и т.д. Различают
2
класса нелин. регрессий:
Регрессии нелин. по аргументу (регрессору), но лин. по искомому пар-ру.
Регрессии нелин. по оцениваемым пар-ам.
Примерами 1-ого класса служат: полиномы различных степеней, гипербола и т.д.
2-ого класса: степенная функция, показательная, экспоненциальная.
1-ый класс реш. обычными методами МНК
Нелин.
регрессии 2-ого класса подразделяются
на линеаризируемые и нелианизируемые.
К линеар. относят регрессии, кот.путем
простых преобразований приводятся к
лин. Например,
![]() –
степенная,
–
степенная,
![]() –
показательная ,
–
показательная ,
![]() - экспоненциальная и т.д.
- экспоненциальная и т.д.
Возможно наличие нелианиз. yt=a+bc+Xt, кот. никакими функцион. преобраз. не приводит к лин. Для оценки используют численные методы. оценка неизвестных параметров нелинейных регрессий первого класса решаются без сложностей методом наименьших квадратов. Наиболее просто они решаются для полиномиальных функций.
Использ.
гиперболич. ф-ции
![]() –
кривая Филипса. При b>0
получ. обратную зависимость, кот. при
Х
–
кривая Филипса. При b>0
получ. обратную зависимость, кот. при
Х![]() ∞
хар-ся нижней асимптотой, т.е.
∞
хар-ся нижней асимптотой, т.е.
![]() .
b<0
получим медленно возраст. ф-цию при Х
∞,
т.е.
.
b<0
получим медленно возраст. ф-цию при Х
∞,
т.е.
![]() - кривая Энгеля.
- кривая Энгеля.
Особый интерес
предст. степенная ф-ия, т.к. b
имеет четкий эконом. смысл, кот. наз.
эластичностью, он показ. на сколько % в
ср-ем изменится рез-т при изменении
регрессора на 1%. В общем случае коэф-т
эласт. для любых
![]() :
:
Э=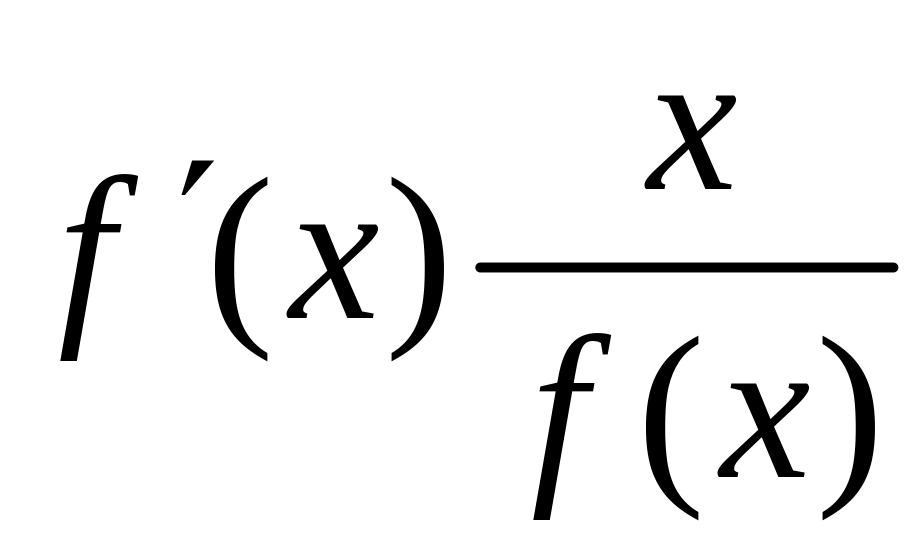 .
Напр, для степенной ф-ии Э=b.Для
др.ф-ий он зависит от x.
.
Напр, для степенной ф-ии Э=b.Для
др.ф-ий он зависит от x.
Для лин.: Э=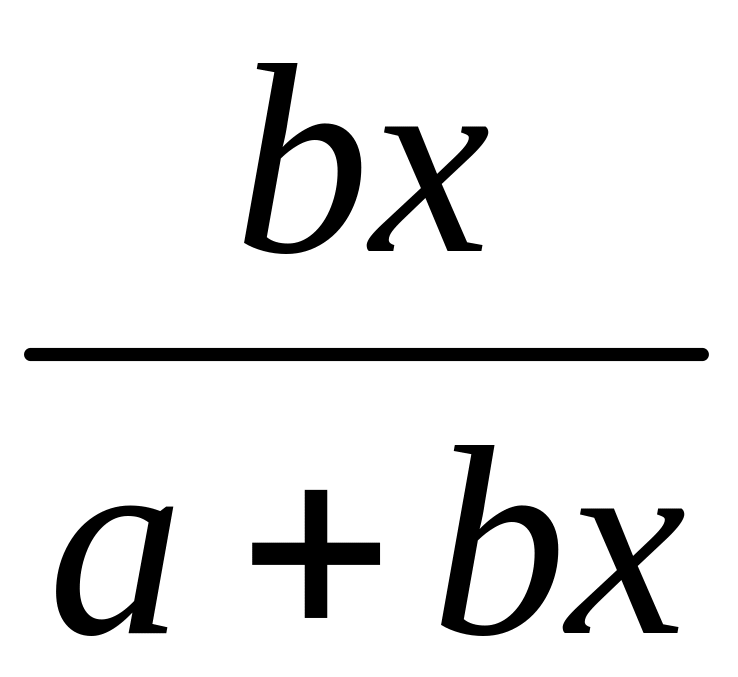 ;
для параболы 2-ого порядка: Э=
;
для параболы 2-ого порядка: Э=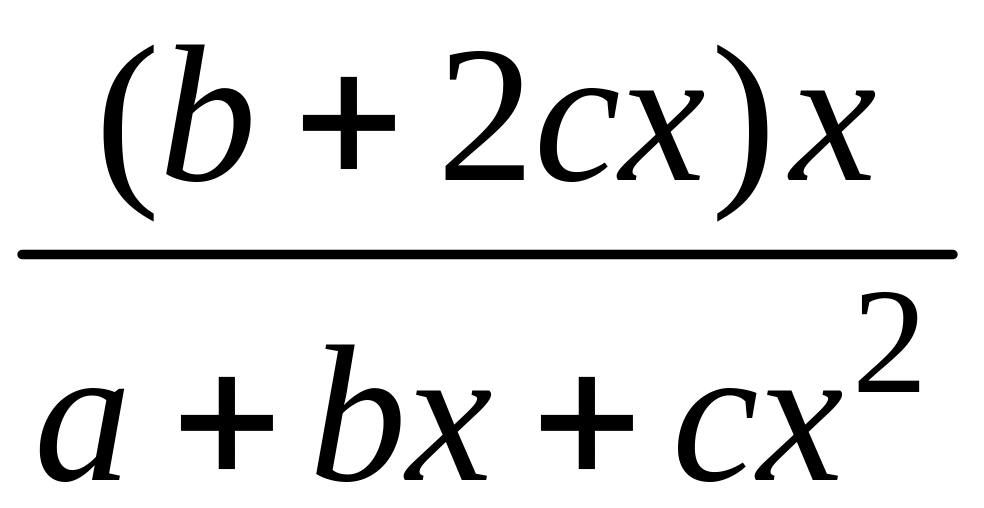 ;
для гиперболы: Э=
;
для гиперболы: Э=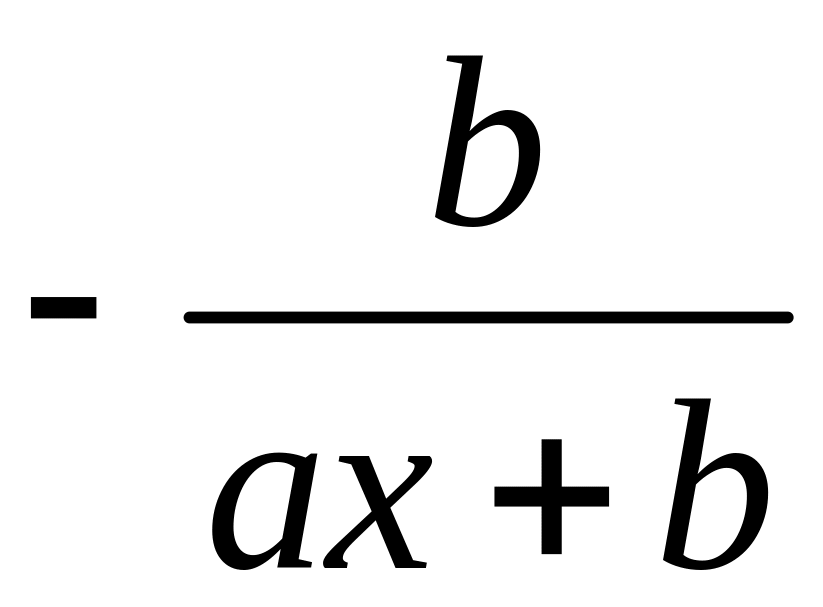 ;
для показательной: Э=
;
для показательной: Э=![]() ;
для полулогарифм(
;
для полулогарифм(![]() ):
Э=
):
Э=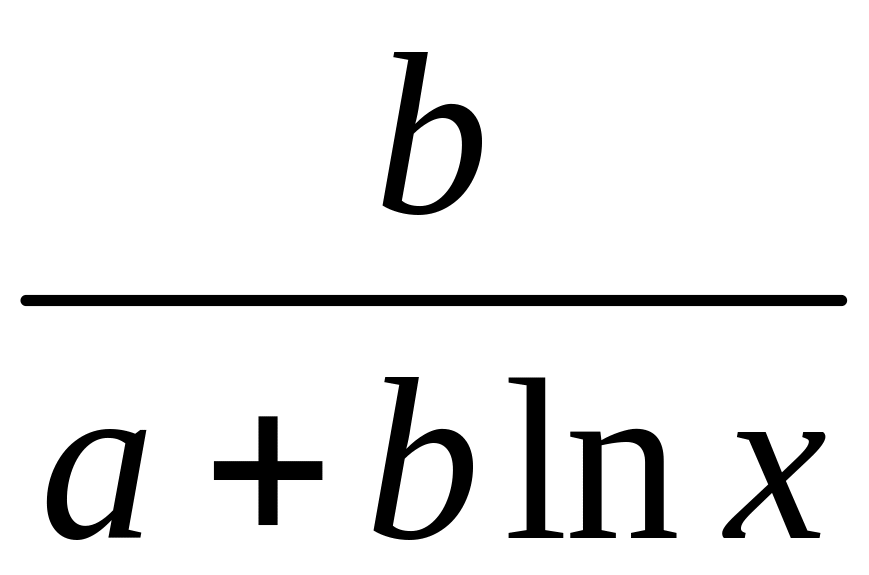 ;
для логист.: Э=
;
для логист.: Э=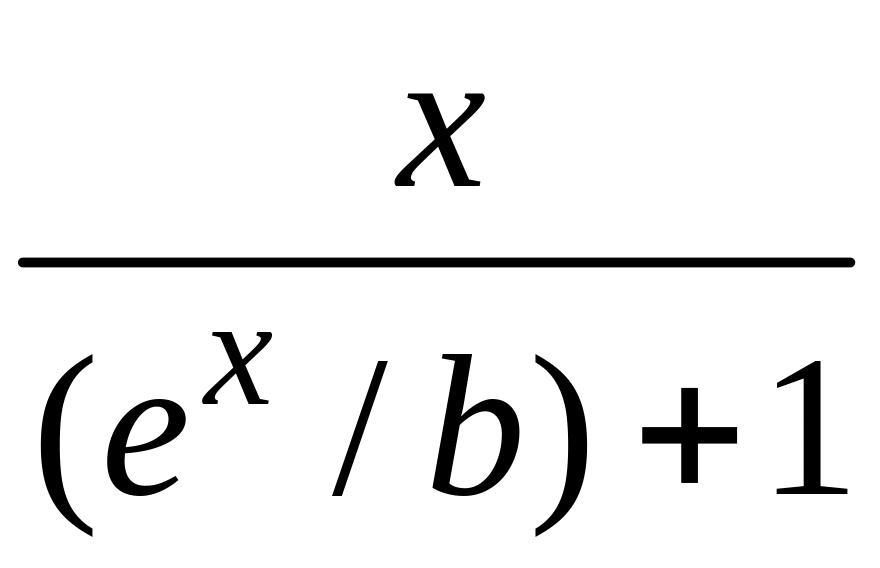 ;
для обратной(
;
для обратной(![]() ):
Э=
):
Э=![]() .
.
Логистическая
ф-ия:
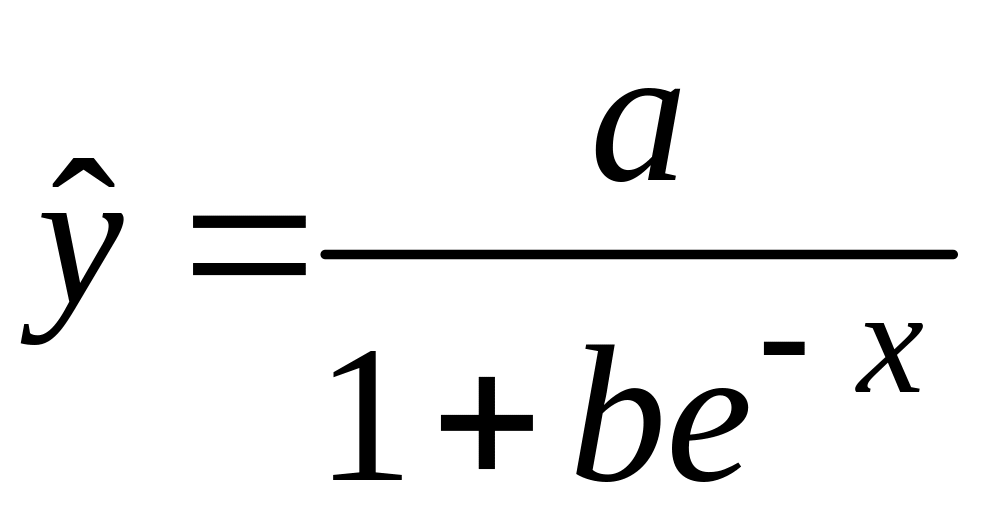 ;
;
15. Корреляция для нелинейной регрессии. Средняя ошибка аппроксимации.
Ур-ние нелин. регрессии, так же как и в лин. зав-ти, дополняется показателем корреляции, а именно индексом корреляции R:
![]()
где σ2общ — общая дисперсия результативного признака у; σ2ост — остаточная дисперсия, т.к..
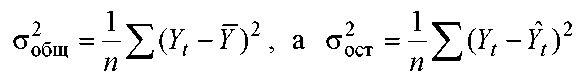
то индекс корреляции можно выразить как

Величина данного показателя находится в границах: 0<R<1, чем ближе к единице, тем теснее связь рассм-ых признаков, тем более надежно найденное уравнение регрессии.
Если нелинейное относительно регрессора урн-ие явл. лин. по искомым пар-м, то для оценки тесноты связи может быть использован лин. коэф-т корреляции для преобраз-ых данных и его величина совпадет с индексом корреляции Ryx = ryz, где z преобразованная величина признака-фактора.
Обратимся для
примера к гиперболе Ŷt=a+b/Xt,
zt=1/Xt,
Ŷt=а+bzt,
для кот. может быть опр-н лин. коэф-т
корреляции: rYZ
=bσz/σy
или r2YZ
=b2σ2z/σ2y
при этом
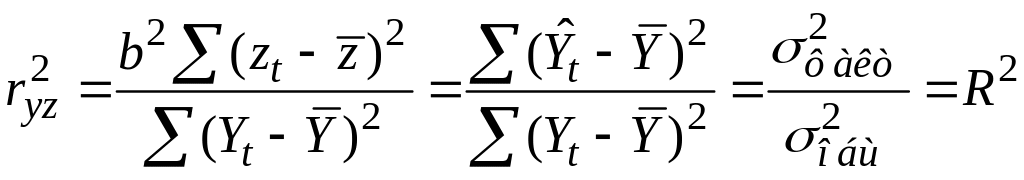
Если при переходе в лин. форму происходит изменение результирующей переменной, то коэф-т корриляции по преобраз. знач. дает приближ. оценку тесноты связи и не совпадает с индексом корриляции.
R2
имеет тот же смысл, что и коэф-т детерминации
![]() .
Он может использоваться для проверки
существенности ур-ния регрессии в целом
по F-критерию
Фишера:
.
Он может использоваться для проверки
существенности ур-ния регрессии в целом
по F-критерию
Фишера:
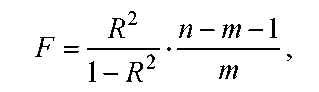
где R2 — индекс детерминации; n — число наблюдений; m — число параметров при переменных х.
Если
![]() то возможна применение линейной
регрессии. Если >0,1,то проводится оценка
существенности и различия вычесленных
по одним и тем же данным через t-критерий
Стьюдента.
то возможна применение линейной
регрессии. Если >0,1,то проводится оценка
существенности и различия вычесленных
по одним и тем же данным через t-критерий
Стьюдента.
![]() ,
где S – ошибка модуля разности.
,
где S – ошибка модуля разности.
![]() .
Если вычисленное значение t>tкр,
то различия м/у R2
и r2
cущественны.
И замена невозможна. (t<2, то различия
несущественны)
.
Если вычисленное значение t>tкр,
то различия м/у R2
и r2
cущественны.
И замена невозможна. (t<2, то различия
несущественны)
Средняя ошибка аппроксимации
Фактические
знач. результативного признака отлич.
от теор.,
рассчитанных по ур-ию
регрессии, т.е. yt
и
![]() .
Величина отклонений фактич.
и расчетных знач.
результативного признака (
.
Величина отклонений фактич.
и расчетных знач.
результативного признака (![]() )
по каждому наблюдению t
представляет собой ошибку аппроксимации.
Их число соответствует объему совокупности.
)
по каждому наблюдению t
представляет собой ошибку аппроксимации.
Их число соответствует объему совокупности.
Для сравнения используются величины отклонений, выраж. в % к фактич. знач. Поскольку ( ) может быть как полож., так и отриц., то ошибки аппроксимации для каждого наблюдения принято определять в %-ах по модулю.