1 Гиперболические функции. Дифференцирование и интегрирование гиперболических функций
Гиперболи́ческие фу́нкции — семейство элементарных функций, выражающихся через экспоненту и тесно связанных с тригонометрическими функциями. Определение
Определение гиперболических функций через гиперболу
Гиперболические функции задаются следующими формулами:
гиперболический синус:
(в
англоязычной литературе обозначается 
)
гиперболический косинус:
(в
англоязычной литературе обозначается 
)
гиперболический тангенс:
(в
англоязычной литературе обозначается 
)
гиперболический котангенс:
Иногда также определяются
гиперболические секанс и косеканс:
[править]Геометрическое определение
Параметризация гиперболического синуса (анимация).
Ввиду
соотношения 
гиперболические
функции дают параметрическое
представление гиперболы 
(
, 
).
При этом аргумент 
,
где 
—
площадь криволинейного треугольника 
,
взятая со знаком «+», если сектор лежит
выше оси 
,
и «−» в противоположном случае. Очевидно,
что и гиперболические функции определяются
через этот параметр, например, уравнения
гиперболического синуса в параметрической
форме: 
,
где 
—
ордината точки гиперболы, соответствующей
площади
.
Это определение аналогично определению
тригонометрических функций через
единичную окружность, которое тоже
можно построить подобным образом.
[править]Свойства
[править]Связь с тригонометрическими функциями
Гиперболические функции выражаются через тригонометрические функции от мнимого аргумента.
.
.
Функция Гудермана связывает тригонометрические функции и гиперболические функции без привлечения комплексных чисел.
[править]Важные соотношения
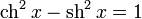(Тождество)Чётность:
Формулы сложения:
Формулы двойного угла:
Формулы кратных углов:
Произведения
Суммы
Формулы понижения степени
Производные:
Интегралы:
2 Определение числового Ряда.Сходимость и сумма числового ряда Числовой ряд — это числовая последовательность, рассматриваемая вместе с другой последовательностью, которая называется последовательностью частичных сумм (ряда).
Рассматриваются числовые ряды двух видов
Определение
Пусть 
— числовая
последовательность;
рассмотрим наравне с данной
последовательностью последовательность
каждый элемент которой представляет собой сумму некоторых членов исходной последовательности. В наиболее простом случае используются обычные частичные суммы вида
Вообще, для обозначения ряда используется символ
поскольку здесь указана исходная последовательность элементов ряда, а также правило суммирования.
В соответствии с этим говорится о сходимости числового ряда:
числовой ряд сходится, если сходится последовательность его частичных сумм;
числовой ряд расходится, если расходится последовательность его частичных сумм:
числовой ряд сходится абсолютно, если сходится ряд из модулей его членов.
Если числовой ряд сходится, то предел последовательности его частичных сумм носит название суммы ряда:
Сумма
числового ряда 
определяется
как предел, к которому стремятся суммы
первых n слагаемых ряда,
когда n неограниченно
растёт. Если такой предел существует и
конечен, то говорят, что ряд сходится,
в противном случае — что он расходится[1].
Элементы ряда 
представляют
собой либо вещественные,
либокомплексные
числа.